下载掌阅APP，畅读海量书库
立即打开
对声学波动方程（1-17）进行傅里叶变换即可得到亥姆霍兹方程：
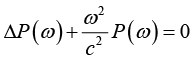（1-43）
或写成：
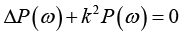（1-44）
其中，波数 k=ω / c 。
下面针对声学中常用的几个物理量进行简要介绍。
通过对波动方程的分析，可以得到空气粒子声学速度 v j 与声压梯度的关系：
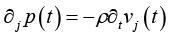（1-45）
对上式进行傅里叶变换，可得到声压梯度与粒子声学速度的频谱关系：
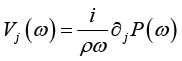（1-46）
在空间某一点，沿某个指定方向上的声阻抗率，其定义为声压与速度频谱（复数）之比：
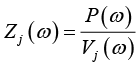（1-47）
其中， j 表示方向。如果希望描述声学边界条件对声波的吸收，则可以使用边界条件的法向声阻抗率：
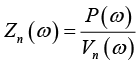（1-48）
绝对刚性壁面具有无限大的阻抗率（ V n = 0， Z n = ∞），而一个绝对柔性的表面（ p = 0）其阻抗率为0。声阻抗率的倒数称为声导纳：
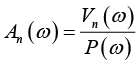（1-49）
可见，阻抗率（或导纳）将声压频谱与速度频谱联系在一起。而声压与速度的时域信号之比并无明显物理意义。阻抗一般来说是针对某物理现象的频域的概念。如在电学中，阻抗表示对交流电的阻碍（电压与电流之比）。在结构动力学中，阻抗有若干种定义：力与位移之比、力与速度之比或力与加速度之比。阻抗永远是一个比值，用来关联一个现象的起因（力、电压、声压）及其结果（位移、电流、声学速度）。一般来说，阻抗是一个随频率变化的复数。
在声压为
p
(
t
)的声波中，空气粒子以速度
v
(
t
)振动。这样的振动需要能量的支持（或者说单位面积的能量），可以用瞬时声强
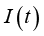表示，即声压与速度的乘积：
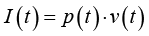（1-50）
在频域中，声强的频谱为：
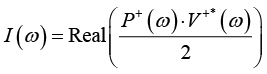（1-51）
将阻抗率写成复数的形式 Z = Z r + i Z i ，就可以将声强频谱写成如下形式：
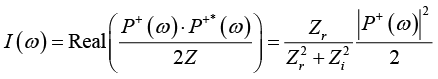（1-52）
上式表明了声强和声阻抗率的实部符号相同。