




确保数据不会被未经授权的用户查看。加密是实现机密性要求的常用手段,也是密码学提供的最基本的安全服务。
它有两个子任务。
● 身份认证。确保用户的身份信息是真实可靠的。
● 信息认证。确保信息来源的真实性。
确保信息没有以未经授权的方式被更改,其中包括意外事件和故意事件,例如停电造成的网络中断导致数据上传不完整或者攻击者篡改信息。密码学可提供一些方法来检测信息是否被篡改。
确保无论是发送方还是接收方都不能抵赖已传输的信息。换句话说,不可否认性是指确保信息的发送方不能向第三方否认他发送了这些数据。
机密性、认证、完整性和不可否认性这 4 点构成了密码学的基本要素,是密码学的基石。在设计密码及对密码的安全性进行测试时都会把以上基本要素作为考虑的重点,全面地思考所面对的问题,如图 1-7 所示。
随着 Enigma 密码被破译,人们才意识到其实真正保证密码安全的重点往往不是算法,而是密钥管理。即使算法外泄,但只要密钥保密,密码就不会失效。这也称为柯克霍夫原则:即使密码系统的任何细节都已公开,只要密钥未泄露,则该密码系统也应是安全的。
在密码学领域,用于解决复杂问题的步骤通常称为算法(Algorithm)。从明文转密文的方法称为 “加密算法”;从密文转明文的方法,则称为 “解密算法”。加密、解密算法合在一起统称为密码算法。
在了解具体算法之前,首先需要了解一些关于密码学的基本概念。

图1-7 密码学基本要素
● 明文 (Plaintext):加密前的信息,需要使用某种密码对其进行变换,以隐藏信息。用
 表示,该信息只有通信双方能看到。
表示,该信息只有通信双方能看到。
● 密文 (Ciphertext):加密后的信息,经过变换后,该信息不能被非授权者所知。用
 表示,该信息所有人都能看到。
表示,该信息所有人都能看到。
● 加密 (Encryption):通过特定的加密技术将明文转化为密文的行为。
● 解密 (Decryption):由掌握加密技术的特定人群将密文转化为明文的行为。
● 发送方/发件人 (Sender):例如后文例子中的 Alice。
● 接收方/收信人 (Receiver):例如后文例子中的 Bob。
● 攻击者/拦截者(Attacker):例如后文例子中的 Eve。
● 密钥 (Key):用
 表示,密钥通常是一系列数字或符号,发送方采用密钥来加密信息,接收方通过相同或不同的密钥来解密信息。只使用一次的密钥称为一次性密钥。
表示,密钥通常是一系列数字或符号,发送方采用密钥来加密信息,接收方通过相同或不同的密钥来解密信息。只使用一次的密钥称为一次性密钥。
● 密钥空间 (Key Space):密钥的所有可能,或解密密钥的可能数量。对于一个安全的密码系统,其密钥空间须能抵御穷举攻击。
Alice 和 Bob 最早出现在1978年 Rivest 等 3 人发表的论文 “A method for obtaining digital signatures and public-key cryptosystems”(一种实现数字签名和公钥密码系统的方法) [7] 中。在此之前,密码学领域一般用 A 表示数据发送方,用 B 表示数据接收方。相对于冰冷的 A 和 B,Alice 和 Bob 更加人性化,因此在密码学界广泛使用,可以说他们是密码学界的 “李雷” 和 “韩梅梅”。不过实际使用过程中,Alice 和 Bob 并不一定是人,在大多数情况下,Alice 是一台计算机,Bob 是一台网络服务器,它们之间互相通信。不过 Eve作为攻击者经常是一个人。Alice 和 Bob 之间互相通信的流程如图 1-8 所示。

图1-8 密码流程
在相关书籍或文献中,还有其他几种身份,如 Mallory、Trent、Victor。Mallory 通常指主动攻击者,它会进行妨碍通信、伪造信息等操作;Trent 则指可信的第三方,进行中继等操作;Victor 指验证者,进行信息验证。
加密的方法主要有两种,分别为替换(Substitution)加密和换位(Transposition)加密。替换加密主要是指将
 个字符的明文替换成
个字符的明文替换成
 个字符的密文;换位加密主要是指将原始信息的字符按照某些特定的模式重新排列。而现代加密方式是以上两种的混合,使得密码更加安全。
个字符的密文;换位加密主要是指将原始信息的字符按照某些特定的模式重新排列。而现代加密方式是以上两种的混合,使得密码更加安全。
加密和解密过程即 Alice 通过密钥加密明文,将明文转变成密文;通过选定途径,发送给 Bob;Bob 通过密钥进行解密,得到明文。一个密码系统,通常由明文
 、密钥
、密钥
 、密文
、密文
 、加密算法
、加密算法
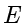 (Encrypt)和解密算法
(Encrypt)和解密算法
 (Decrypt)这 5 种元素构成,加密算法用公式表示为:
(Decrypt)这 5 种元素构成,加密算法用公式表示为:

解密算法用公式表示为:

使用密码的场景一般是发送方和接收方之间没有安全的通信通道,所以需要加密信息,以确保不会被第三方知道。信息安全的关键是攻击者不知道加密中使用了何种特定密钥,以及加密方式。攻击者一旦知道密钥及加密方法,密文即被破译。
现代密码学有 3 个基本原则。
(1) 安全的定义
对安全的定义必须是公式化的、表述严格且精确的。一个安全的密码算法应该满足哪些条件?“对于攻击者而言,不能恢复密钥。”这句话是否满足对于安全的定义呢?很显然,不满足。因为有些算法即使不能恢复密钥,也有可能泄露明文。比如
 ,没有人可以从密文中猜出密钥,但明文依然被泄露。“对于攻击者而言,不能从密文恢复完整的明文。”这也不满足对于安全的定义。因为不需要恢复完整明文,只要恢复部分明文就可能泄露重要的信息。比如,某个加密算法只加密偶数位的信息,那么奇数位的信息依然会被泄露。“对于攻击者而言,不能从密文恢复任何明文字符。”这也不满足对于安全的定义。因为即使攻击者不能知道明文的任何信息,但只要知道明文之间潜在的关系即可。比如,虽然不知道两架飞机的具体速度,但是知道飞机 A 比飞机 B 快,这也是信息泄露,是不安全的。
,没有人可以从密文中猜出密钥,但明文依然被泄露。“对于攻击者而言,不能从密文恢复完整的明文。”这也不满足对于安全的定义。因为不需要恢复完整明文,只要恢复部分明文就可能泄露重要的信息。比如,某个加密算法只加密偶数位的信息,那么奇数位的信息依然会被泄露。“对于攻击者而言,不能从密文恢复任何明文字符。”这也不满足对于安全的定义。因为即使攻击者不能知道明文的任何信息,但只要知道明文之间潜在的关系即可。比如,虽然不知道两架飞机的具体速度,但是知道飞机 A 比飞机 B 快,这也是信息泄露,是不安全的。
正确的定义是:若攻击者无法从密文中计算出任何关于明文的信息,那么该密码是安全的。
(2)精确的假设
若密码学系统的安全性依赖于未被证明的假设,这种假设必须被精确陈述,且假设需要尽可能的少。大部分公钥密码系统通常是基于数学困难问题构造的。现代密码学要求,若一个方案的安全性依赖于假设,则假设必须被精确地陈述。假设是暂无数学证明的,但据推测是正确的命题。一个假设被检查和测试的次数越多,那么它的可信度就越高。
在其他条件相同的情况下,如果有两个基于不同假设的方案都被证明满足某种定义,那么该选哪种方案呢?通常选择假设更弱的那个方案。这是因为假设越弱越好,越弱的假设,其所需要的条件就越少,需要的信息也越少,也就越安全。反过来说,如果某个假设需要很强的条件才可以成立,那么这个假设就会因为条件太多而带来更多的不安全因素。
(3) 严格的安全证明
密码学方案应该有严格的安全证明。一个密码学方案在某些特定的假设下满足给定的定义,是可以严格证明该方案安全的前提。即假设 A 是正确的,则根据 A 给定的定义,所发明的算法 B 就是安全的。假设否定了 A,那么攻击者就能破解算法 B。
要保证整个密码系统的安全,需要什么呢?只保证加密算法的安全就行了吗?答案是否定的。加密算法的设计需要经严格测试以证明其安全性。比如好不容易设计了一个加密算法,但只能加密前 10 位的字符,后面的不能加密,这很明显不是一个安全的加密算法。一个安全的加密算法应该是无法从密文中计算出任何关于明文的信息,换句话说,不光不能算出具体的明文信息,也不能算出与明文相关的信息。
不过遗憾的是,大多数的密码并不能保证密文中没有明文的任何信息。
在未知密钥的情况下,从截获的密文中分析出明文的过程称为密码分析。试图对密码进行分析的行为称为攻击。
密码分析作为密码学的一部分,通常情况下指的是一种破译密码的方法。绝大多数的密码分析方法都是由学术界赫赫有名的密码学家完成的。它的难度不比设计密码算法小,它的意义在于让人们试图破译密码以验证该密码算法是否安全,如果发现漏洞,需要及时补上,或者更换更安全的密码。
密码分析通常有 3 种方法,如下所述。
经典密码分析(Classical Cryptanalysis)包括两种,一种是纯暴力破解,穷举所有明文的可能性,找出最合理的一种;另一种则是数学分析方法,包括以下 4 种攻击方式。
● 唯密文攻击 (Ciphertext-Only Attack):攻击者仅通过分析密文来恢复明文。
● 已知明文攻击 (Known-Plaintext Attack):攻击者通过分析已知的明文-密文对来恢复全部明文。
● 选择明文攻击 (Chosen-Plaintext Attack):攻击者知道加密算法,并且有能力选择一些明文一密文对来恢复全部明文。
● 选择密文攻击 (Chosen-Ciphertext Attack):攻击者可以选择部分密文并获得相应明文,是一种比已知明文攻击更强的攻击方式。
这 4 种攻击的攻击难度依次递减。
实施攻击(Implementation Attack)即不利用密码算法本身,而是通过其他渠道进行密码分析。例如通过测量处理明文的 CPU 功耗,或者测量信号强度来推理出密钥,这些方式也称为侧信道攻击。除此之外还有软硬件攻击、弱点攻击、差分攻击等方式,甚至包括清除访问记录。实施攻击在绝大多数情况下针对的是攻击者可以物理访问的密码系统,因此如果使用远程系统加密,通常不会考虑这种方法。
通过间谍行为,如行贿、窃取、跟踪等方式获得密钥,称为社会工程学攻击(Social Engineering Attack)。它包括但不限于钓鱼、恶意软件传播、身份伪造、诱饵攻击、尾随、假冒权威等攻击方式。有个笑话:某公司被黑客勒索,每 20 分钟断一次网,用技术手段怎么也找不到原因。最后发现是黑客收买了保安,让他每 20 分钟拔一次网线。这种攻击方式也是社会工程学攻击的一种。
密码系统的安全性分析评估一般需要用数据复杂度(明文空间、密文空间、密钥空间)、时间复杂度、空间复杂度和成功概率来衡量。一般来说,密码分析常说的计算复杂度主要是指时间复杂度和空间复杂度。
攻击者 Eve 会寻找密码使用过程中最脆弱的环节,不仅限于算法,还包括密码传输、管理等。换句话说,密码使用者必须使用足够安全的算法,也必须保证可以抵御实施攻击和社会工程学攻击。本书将会重点介绍经典密码分析方法,也会简单介绍实施攻击和社会工程学攻击。
对于任何安全的加密方案,其密钥空间
 必须能抵御穷举攻击,且必须满足
必须能抵御穷举攻击,且必须满足
 ,即明文空间大于密钥空间。若可能的明文比可能的密钥还少,穷举出所有可能的密钥,解密之后会获得比明文空间还大的候选明文集合。
,即明文空间大于密钥空间。若可能的明文比可能的密钥还少,穷举出所有可能的密钥,解密之后会获得比明文空间还大的候选明文集合。
充分大的密钥空间是密码算法安全的必要不充分条件。一个安全的密码算法一定有一个充分大的密钥空间,但充分大的密钥空间不一定能保证密码算法的安全。还有一点值得注意,密钥空间并不等于密钥长度。密钥长度为密钥的二进制位数,比如密钥为 10101010 ,一共 8 位,那么它的密钥长度就是 8 ,其密钥空间为
 。如果密钥长度为 16 ,是 8 位密钥长度的两倍,那么它的密钥空间会远远大于后者的密钥空间大小,是其
。如果密钥长度为 16 ,是 8 位密钥长度的两倍,那么它的密钥空间会远远大于后者的密钥空间大小,是其
 倍之大。
倍之大。
本书将会讨论对称密码学(Symmetric Cryptography)和非对称密码学(Asymmetric Cryptography),非对称密码学也称公开密钥密码学(Public-Key Cryptography),简称公钥密码学。
在古典密码学中,收发双方都是秘密地选择密钥,密钥绝不能被公开。然后根据选择的密码算法,规定加密和解密过程,并且加密过程和解密过程是相同的。因此如果攻击者知道了密钥和加密算法,就容易解密信息,从而泄露信息。因为加密和解密过程是相同的,所以被称为对称加密算法。
对称加密算法有以下几个特点。
● 加密和解密使用的是同一个密钥。
● 加密和解密的速度比较快。
● 密钥交换的渠道不安全,容易被攻击。可能会产生为了保护密钥不被泄露,而用密码系统加密密钥的无解事件。
● 为了安全,可能需要长密钥来保护信息,这对密钥的管理者提出了非常高的要求,密钥管理起来非常困难。因此在网络通信中,较少使用对称加密算法。
对称加密算法就好比 Alice 和 Bob 都有一串相同的钥匙。Alice 把信息放在一个保险柜里,然后锁上。如果 Bob 想要知道这个信息,就需要用钥匙打开这个保险柜。但是让 Alice 和 Bob 拥有一串相同的钥匙就比较麻烦。当面交换和确认固然是个好办法,但是次数多了就很麻烦。放在保险柜里给对方?但没有钥匙就无法打开保险柜。而且用户一旦不止两个人,需要使用的钥匙对就多了,钥匙分配起来就比较麻烦。并且还有一点,就是拿 Bob 的钥匙开保险柜的人,不能确定就是 Bob 本人,也有可能是 Eve 拿他的钥匙开的,这没办法验证。
当然,利用计算机可以在一定程度上克服这些困难,诸如 DES 和 AES 就是对称密码学的巅峰之作。
为了解决上述难题,人们发明了非对称密码学。非对称密码学使得安全性得到了巨大提高。它将密钥一分为二,拆分成了公钥 (Public Key) 和私钥 (Private Key) 两组密钥。顾名思义,公钥可以被任何人知道,私钥则不能被泄露,只有接收方 Bob 知道。任何人都可以使用公钥加密信息,但只有拥有私钥的 Bob 才能解密信息。这就是非对称加密。比如, Alice 向银行请求公钥,银行将公钥发送给 Alice,Alice 使用公钥对信息加密,那么只有私钥的持有人——银行(Bob)才能对 Alice 的信息解密。与对称加密不同的是,银行不需要将私钥通过网络发送出去,这就解决了密钥交换的问题,因此安全性大大提高。
对称加密算法和公钥加密算法所要求的密钥长度完全不同。对攻击方来说,他极有可能通过穷举找出密钥,因此攻击方肯定对密钥空间的大小感兴趣。大多数密码系统的密钥空间大小是固定的。部分对称算法(如 AES)会根据用户需求来提供相应的模式,每种模式会对应不同的密钥长度。而公钥加密算法(如 RSA)也可以根据需求,提供不同的密钥长度。目前,对于一个只拥有 64 位密钥长度的密码系统,如果靠穷举攻击,在现代计算机的帮助下,几天即可破解。而对于拥有 128 位密钥长度的密码系统,只靠穷举攻击,则需要几十年的时间。破解一个 256 位密钥的加密算法,则需要成千上万年。