




根据上面的数论知识,可以得到模运算的一个基本定理——欧拉定理。它与欧拉函数紧密相关,但概念不同。欧拉函数描述的是小于或等于
 的正整数中与
的正整数中与
 互素的数的数目;欧拉定理在数论中是一个关于同余的性质,该定理被认为是数学世界中最美妙的定理之一,这是一个既优美且非常有用的结果。
互素的数的数目;欧拉定理在数论中是一个关于同余的性质,该定理被认为是数学世界中最美妙的定理之一,这是一个既优美且非常有用的结果。
定理2.7.1 欧拉定理(Euler’s Theorem)
如果
 ,且
,且
 ,那么:
,那么:

其中
 为欧拉函数。
为欧拉函数。
例
2.7.1
证明
 。
。
解:
很显然,使用欧几里得算法可以算出,
 ,因此,
,因此,


定理2.7.2 模的幂运算
如果
 是非负整数并且满足
是非负整数并且满足
 ,那么:
,那么:

证明

例
2.7.2
求
 的值。
的值。
解:

幂运算非常简单,很容易计算。比如计算
 ,可以列出
,可以列出
 ,只需要计算 15 次乘法就能得到答案。但是如果指数是一个大数,比如 1000000000 ,那么求这种高次幂的最小正整数模应该怎么办呢?对于这种大数,挨个计算就太复杂了,会降低加解密的效率。为了提高效率,就必须想办法在计算的过程中用最少的步骤来快速达到指定的指数。
,只需要计算 15 次乘法就能得到答案。但是如果指数是一个大数,比如 1000000000 ,那么求这种高次幂的最小正整数模应该怎么办呢?对于这种大数,挨个计算就太复杂了,会降低加解密的效率。为了提高效率,就必须想办法在计算的过程中用最少的步骤来快速达到指定的指数。
想快速得到幂运算的结果就需要用到二进制。当指数使用二进制表示时,只有 0 和 1可以作为系数出现,这意味着每个正整数都可以表示为 2 的不同幂的和。还是以
 为例,十进制转二进制的方法如例 1.3.1 所示。利用平方,可以快速得到结果:
为例,十进制转二进制的方法如例 1.3.1 所示。利用平方,可以快速得到结果:

仅需 4 次计算就能得到结果。相比进行 15 次重复运算,大大节约了时间。
如果幂不是 2 的倍数呢?比如
 ,应该如何计算?其实也很简单,拆分计算即可:
,应该如何计算?其实也很简单,拆分计算即可:

这样也仅需 6 次就可以得到答案。
例
2.7.3
上面例子的计算较简单,不使用相关公式也可以计算。如果是

 ) 这种大数模的幂运算呢?在通常的运算过程中人们都不想处理大数,因为这时候计算太繁琐。此时可应用幂取模运算的办法。
) 这种大数模的幂运算呢?在通常的运算过程中人们都不想处理大数,因为这时候计算太繁琐。此时可应用幂取模运算的办法。
解:
第 1 步,将
 中的指数
中的指数
 转化为二进制数。
转化为二进制数。

用 Python 代码可写成:
1 #二进制数
2 number = 2641
3 number_bin = bin(number)[2:]
4 cov_number_bin = bin(number)[2:][::-1]
5
6 sum_number = ''
7 for i in range(len(cov_number_bin)):
8 if cov_number_bin[i] == '1':
9 if sum_number == '':
10 sum_number += str(2**(i))
11 else:
12 sum_number += ' + ' + str(2**(i))
13 print(sum_number)第2步,用重复平方(Repeated Squaring)得到幂的余。
因为
 ,因此
,因此
 ,得到 3278564 后继续使用
,得到 3278564 后继续使用
 作为
作为
 的基本单位。不用直接计算
的基本单位。不用直接计算
 ,只需要计算
,只需要计算
 。得到 1631541 后又可以继续应用在
。得到 1631541 后又可以继续应用在
 上,使得
上,使得
 。以此类推,以减少运算量,得到所有
。以此类推,以减少运算量,得到所有
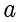 的 2 次幂项的余:
的 2 次幂项的余:

第 3 步,将第 1 步得到的幂次相乘。

Python 计算过程如下,速度比 Python 的运算符
 快,因为无须重复计算。下面的函数等同于 Python 内置函数
快,因为无须重复计算。下面的函数等同于 Python 内置函数
pow(a,n,p)
。
1 def fastExpMod(a, n, p):
2 result = 1
3 while n != 0:
4 if (n&1) == 1:
5 # ei = 1, then mul
6 result = (result * a) % p
7 n >>= 1
8 # a, a^2, a^4, a^8, ... , a^(2^n)
9 a = (a*a) % p
10 return result
因此,如果
 是正整数,计算
是正整数,计算
 的时间复杂度大约为
的时间复杂度大约为
 。
。
欧拉定理除了可以用于快速求大数幂运算的模,还可以用于求逆元。当
 时,因为根据欧拉定理
时,因为根据欧拉定理
 ,同乘
,同乘
 可以得到
可以得到
 ,等式两边调换一下位置得到:
,等式两边调换一下位置得到:

如果
 为素数,那么就很容易得到:
为素数,那么就很容易得到:

例
2.7.4
计算
 、
、
 。
。
解:
计算
 。因为
。因为
 ,且 997 是素数,所以:
,且 997 是素数,所以:

计算
 。因为
。因为
 ,所以可以用欧拉定理。但 151255 不是素数,所以需要计算
,所以可以用欧拉定理。但 151255 不是素数,所以需要计算
 。首先
。首先
 ,因此可以很容易算出:
,因此可以很容易算出:

那么:


 求解
求解
下面考虑一个方程:

其中
 是已知整数,需要求解变量
是已知整数,需要求解变量
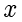 。这个方程在后面介绍的 RSA 加密系统中有至关重要的作用。一般情况下,这个方程比较难解,但如果
。这个方程在后面介绍的 RSA 加密系统中有至关重要的作用。一般情况下,这个方程比较难解,但如果
 是一个素数,那么就会变得较容易了。
是一个素数,那么就会变得较容易了。
令
 为素数,
为素数,
 且为整数,若满足
且为整数,若满足
 。此时就存在一个整数
。此时就存在一个整数
 ,使得:
,使得:

将方程
 改写成:
改写成:

如何求解这个方程呢? 需要考虑两种情况,首先假设
 ,那么就得到
,那么就得到

 ,很容易求得
,很容易求得
 。
。
假设
 ,由于
,由于
 ,那么就有
,那么就有
 ,
,
 。并且因为
。并且因为
 是素数,所以
是素数,所以
 ,就有
,就有
 。该结论也称费马小定理,将在定理 7.5.3 中详细介绍并证明。引用这个定理,继续推导可得出:
。该结论也称费马小定理,将在定理 7.5.3 中详细介绍并证明。引用这个定理,继续推导可得出:

此时就很容易发现,方程
 的唯一解为:
的唯一解为:

例 2.7.5 求解下列方程:

解:
由于 8017 是一个素数,为了求解,可以转化成另一个关于求解
 的方程:
的方程:

那么根据欧拉定理,就有
 。代入公式,就可以得到:
。代入公式,就可以得到:
