




默比乌斯函数由德国数学家默比乌斯(August Ferdinand Möbius)提出。在数论中,经常出现像欧拉函数这种定义在正整数集上的实值或负值函数,这类函数称为数论函数。当
 ,且
,且
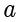 和
和
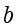 互素时,有
互素时,有
 。具有这种性质的数论函数称为积性函数(Multiplicative Function)。下面将介绍另外一个重要的积性函数,即默比乌斯函数。
。具有这种性质的数论函数称为积性函数(Multiplicative Function)。下面将介绍另外一个重要的积性函数,即默比乌斯函数。
定义2.6.1 默比乌斯函数 (Möbius Function)
默比乌斯函数 [9] :

根据默比乌斯函数计算可得前 15 个值,如表 2-5 所示。
表2-5 前 15 个默比乌斯函数值

例
2.6.1
通过例子来解释一下默比乌斯函数是如何运算的。
 ,由相同的素数所得,所以
,由相同的素数所得,所以
 。
。
 也包含相同素数,所以
也包含相同素数,所以
 。而
。而
 ,由不同素数所得,所以是
,由不同素数所得,所以是
 。
。
1 def isPrime(n) :
2 if (n < 2) :
3 return False
4 for i in range(2, n + 1) :
5 if (i * i <= n and n % i == 0) :
6 return False
7 return True
8
9 def mobius(N) :
10 if (N == 1) :return 1
11 p = 0
12 for i in range(1, N + 1) :
13 if (N % i == 0 and isPrime(i)) :
14 if (N % (i * i) == 0) : return 0
15 else : p = p + 1
16 if(p % 2 != 0) : return -1
17 else : return 1定理2.6.1 默比乌斯函数的积性性质
假设
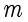 和
和
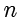 没有公因数。进一步假设
没有公因数。进一步假设
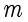 是
是
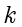 个不同素数的乘积,
个不同素数的乘积,
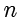 是
是
 个不同素数的乘积。那么
个不同素数的乘积。那么
 就是
就是
 个不同素数的乘积,即:
个不同素数的乘积,即:

由定理 2.6.1 可知,
 ;
;
 ,由于满足素数的平方能整除 360 ,因此
,由于满足素数的平方能整除 360 ,因此
 。
。
那么欧拉函数
 与
与
 有什么关系呢?它们之间的关系可以表示为:
有什么关系呢?它们之间的关系可以表示为:

其中
 为默比乌斯函数的和函数,且
为默比乌斯函数的和函数,且
 ,记作:
,记作:

例
2.6.2
假设整数
 ,则
,则
 ,
,
 ,
,
 ,那么:
,那么:
●

●

●

●


例如,
 ,根据式 (2-44),很容易可以算出:
,根据式 (2-44),很容易可以算出:
