2.4　模运算

2.4.1　模运算定义

模运算也称同余理论（Congruence），由 24 岁的高斯在他的著作《算术研究》中首次提出。模运算得到的结果其实就是除法定理中的余数。在除法定理中，如果用 2 去除一个正整数，很容易知道余数就只有两个，即 0 和 1 ，其中偶数的余数是 0 ，奇数的余数是 1 。如果用 3 去除一个正整数，余数就只有 3 个，即 0、1、2。模运算对除法定理的商不感兴趣，甚至熟悉一些式子后可以忽略，而感兴趣的是余数。

日常生活当中其实就有很多模运算的实际应用。例如，时间上的“星期”也就是关于模 7 的运算。大部分人都只对今天是星期几（余数）感兴趣，很少人对今天是今年的第几周 (商) 感兴趣。如果扩大范围，则所有只对周期性结果感兴趣的事情都是模运算。下面了解模运算的定义。

定义2.4.1　模运算

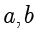设 ， 是一个定值且 。规定当 时， 模 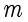同余。记作：

模运算拥有以下几个性质 ^[8] 。

1）反身性。对于所有的 ，都有 。

2) 对称性。对于所有的 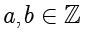，都有 。

3) 传递性。对于所有的 ，如果 且 ，那么 。

对于 ， ，并且 和 ，那么：

●

●

●

●

● 如果 ，

例 2.4.1 模运算例子。

在 Python 中，可以使用 进行模运算，如 。

例 2.4.2 求 。

解： 。阶乘的增长非常可怕，如果没有模运算的帮助，解这道题非常困难。

不过由于 ，因此对于 ，都有：

也就是说：

给定 ， ，如果 ，那么对于线性同余方程 有且只有唯一解。如果 ，方程 则可能有或没有解。如何求解方程 ？过程也非常简单，首先验证 是否可以整除 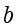，如果不可以，则无解。如果可以，则用下面的方程进行求解。

将式子转化成 ，记作 。使用欧几里得算法得到式子 的解 ，调整得到 。因此最后的解就是 。

例 2.4.3 求方程 和 。

解： 第 1 个方程比较简单，很容易得到 。该解是模 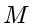情况下的唯一解，如果扩展至模 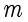，则 是另一个解。

求第 2 个方程，由于 ，可以整除 5 ，因此有且只有唯一解。然后计算 ，计算过程和例 2.3.3 相同，得到结果 。所以该方程最小正剩余 。

其实可以发现，无论模数 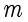多大，得到的值总是小于 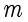。因此模运算可以被看作一个环（Ring），也称为整数模 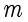的环（关于环的定义见 2.9.2 节），余数在这个环中怎么都跳不出去，最大值是 。记作：

除此之外，当 时，那么就会存在一个关于 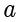的逆元 ，使得 。注意在模运算中， 。下面通过一个例子来了解如何计算 。

例 2.4.4 设模数 ， 。求 。

解： 很明显 ，因为它们都是素数。因此必有 。由于 ，所以 。

同理，如果 ， ，那么 。

因此规定，如果整数 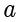存在模 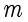的逆元，当且仅当 。记作

也叫整数模 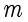乘法群（单位群），该群是数论的基础，在密码学中有非常重要的作用，特别是在素性测试中运用甚广。

例 2.4.5 求 和 。

解： 因为 11 是素数，所以 都与 11 互素，因此很容易得到：

24 是一个合数，所以小于 24 的其他合数都不是它的整数模的单位，因此只能从小于 24 的素数 中选择。而 3 是 24 的一个因子，因此需要排除 3 。经过相似步骤，最后可得：

2.4.2　身份证校验码

在了解模运算后可以进一步了解生活中模运算的应用，比如人们经常会使用的身份证号就含有模运算。

1999年8月26日，中华人民共和国国务院发布《国务院关于实行公民身份号码制度的决定》，规定中国公民身份号码按照《公民身份号码》（GB 11643-1999）进行编制，由 18 位数字组成：前 6 位为行政区划代码（地址码），第7～14位为出生日期码，第 位为顺序码，第 18 位为校验码。整个身份号码组合的方式如表 2-1 所示。

行政区划代码是指公民常住户口所在市（县、镇、区）的识别码。代码编码一共有 6 位数，共 3 层，每层 2 位数。第一层是省级行政区划代码，第二层是地级行政区划代码，第三层是县级行政区划代码。还有第四、第五层行政区划代码，代表乡、村级，但在身份证中不使用。不同地区的行政区划代码可参考《中华人民共和国行政区划代码》（GB/T 2260—2007）。例如 440112 就代表广东省广州市黄埔区， 110108 就代表北京市海淀区。

出生日期码非常好理解，一共 8 位数，前面 4 位是出生公历年，然后是月、日。比如 1999 年 9 月 9 日出生的人的出生日期码就是 19990909。

顺序码一共 3 位数，是给相同行政区划代码和出生日期码的人编定的顺序号，奇数分配给男性，偶数分配给女性。如 223 代表一名男性； 224 代表一名女性。

最后一位校验码则是模运算的经典应用。校验码可以帮助人们在录入身份证号过程中检查号码是否有错误，实现快速检测功能。校验码的计算方法是 MOD 11-2。顾名思义， MOD 就是模运算， 11 则代表模 11，2 是生成元。计算校验码的公式为：

其中 表示第 位（从左至右）身份证号码值， 表示权重系数，计算公式为 。该权重系数是已知的，如表 2-2 所示。

假设有一个人是 2032 年 5 月 19 日出生，并在北京市海淀区上的户口，排在 123 位，那么前 17 位的号码是 。 ，校验码 。

细心的读者可能发现，模 11 的运算有一定的概率会出现值为 10 的结果，如果加入身份证号中，就会变成 19 位，比常规的 18 位数字多出了一位，这显然不符合身份证的设计要求。因此规定，当校验值等于 10 时，就用罗马数字 “X” 代替，使身份证号码位数不超过 18 位。这也是有些人的身份证号码最后一位是“X”的原因。

那么有了校验值后，如何确定身份证号码是否输入正确呢？校验公式如下：

输入身份证号码过程中，如果输入的号码全部正确，那么校验公式就会成立。而如果输错一位数，该校验公式则肯定不成立。

例 2.4.6 检验身份证号 330302204311117880 是否符合要求。

解： 根据身份证号信息可以知道，330302 代表此人户口所在地，20431111代表此人是 2043 年 11 月 11 日出生的， 788 代表此人是一名女性，且上户口的顺序是 788 。那么就需要计算 ，如表 2-3 所示。

根据校验公式 (2-28)，将 求和并模 11，可以得到：

校验公式（2-28）成立，因此该身份证号输入格式是正确的。

最后来探讨一下：为什么选择 11 作为模数，而不是 7、8、9、10、12 或者其他的数字呢？假设选择大于 11 的数字，如 13 ，那么就会多出 10、11、12 这 3 个两位数的数字，为了符合身份证的长度，只能使用字母来代替，比如 X、Y、Z。这并不符合身份证设计理念，增加了理解身份证数字信息的难度，很难对公众进行解释说明。如果是小于 11 的数字，如 7 ，那么就会造成 7、8、9 这 3 个数字的 “浪费”。现在看来， 10 这个数字非常合适，不但没有数字浪费，还可以避免出现 “X” 这样的字母。但为什么不选择 10 作为模数呢？

首要原因是， 10 是一个合数。上面提到，输错一位数，校验公式（2-28）肯定不成立。满足这个条件的前提是模数是一个素数。在例 2.4.6 中， ，如果模数是 10 ，那么 。假设身份证号填错一位数，填成了 330302204311117830 ，那么 。在模 10 的运算下，它们的值都为 3 ，通过了验证，但实际上是错误的。因此素数 11 显然是比合数 10 更为合适的选择。

然而，即使选择 11 作为模数，依然有可能在身份证号填写错误的情况下通过验证。例如身份证号填错的不是一位数，而是两位数，该组身份证号就有可能通过校验公式的校验。在例 2.4.6中，如果填写成 330302204311117530 ，此时 ，就通过了验证。不过由于错误发生的概率不高，因此被视为在可容忍的范围内。同时配合其他方式，如人脸识别、指纹识别进行再次校验，双管乃至多管齐下，便可确保个人身份的精确性和唯一性。 eJuzouo1BFws4Xbf6PAXQkJAeUTxSe8I6rD1YE1QHiPRljSSpsbBhS7/QFXcVESg