




很多人在小学期间就接触过欧几里得算法(The Euclidean Algorithm) [8] ,它就是数学课本中的辗转相除法。它最早出现在欧几里得所著的《几何原本》中,书中不光介绍了平面几何和立体几何,还介绍了一些基础数论的知识,如整除性、素数、最大公约数、最小公倍数等。中国古代学者也发现了辗转相除法,如在《九章算术》中,作者就介绍了约分术。其原文是:“ 约分术日:可半者半之,不可半者,副置分母子之数,以少减多,更相减损,求其等也。以等数约之。 ”大意是给定两个整数,如果它们都为偶数,则将它们减半后再计算;如果不是偶数,则用较大的数减去较小的数,然后将所得差与较小的数组合为一对新的数,再用大数减小数,反复相减直到差数与较小的数相等,这个等数就是最初两个数的最大公约数。
遗憾的是,《几何原本》中的数学知识有明确的概念及严格的推导过程和证明,《九章算术》则没有。因此后世也将辗转相除法称为欧几里得算法。
如果
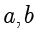 是两个整数,其中至少有一个非零整数,那么
是两个整数,其中至少有一个非零整数,那么
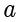 和
和
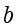 的最大公约数(The Greatest Common Divisor,GCD) 就是能同时除
的最大公约数(The Greatest Common Divisor,GCD) 就是能同时除
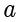 和
和
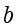 的最大整数,记作
的最大整数,记作
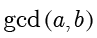 。并且它们有几个性质,如果
。并且它们有几个性质,如果
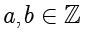 且
且
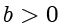 ,那么
,那么
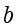 能整除
能整除
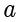 就说明
就说明
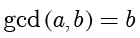 。如果
。如果
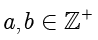 ,在除法定理中,
,在除法定理中,
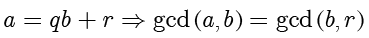 。
。
那么如何找到
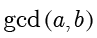 呢? 使用欧几里得算法。
呢? 使用欧几里得算法。
1)设
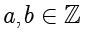 ,并且
,并且
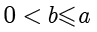 。令
。令
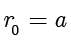 ,
,
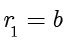 。通过除法定理,可求得:
。通过除法定理,可求得:

2)如果
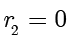 ,显然
,显然
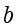 能整除
能整除
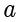 ,因此
,因此
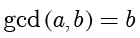 。如果
。如果
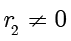 ,那么用
,那么用
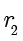 除
除
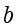 则得到整数
则得到整数
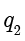 和
和
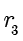 :
:
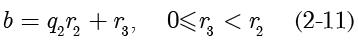
3)如果
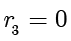 ,显然
,显然
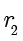 能整除
能整除
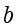 ,因此
,因此
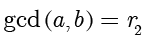 。如果
。如果
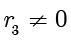 ,那么用
,那么用
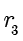 除
除
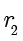 则得到整数
则得到整数
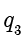 和
和
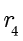 。对于
。对于
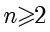 ,可求得:
,可求得:
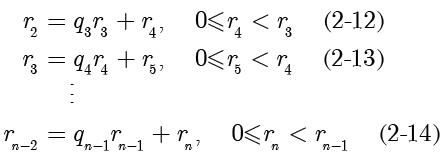
4)继续使用该除法过程直到余数等于 0 为止,最后一个非零余数就是最大公约数
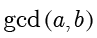 :
:
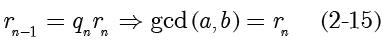
这是因为余数组成的递减序列是
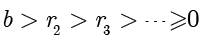 ,不会包含大于
,不会包含大于
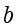 的整数。对于
的整数。对于
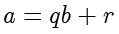 ,有
,有
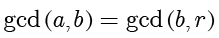 。因此
。因此
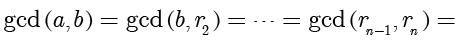
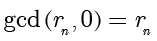 。
。
如果
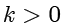 ,那么
,那么
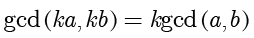 。以下展示两个计算最大公约数的示例。
。以下展示两个计算最大公约数的示例。
例
2.3.1
计算
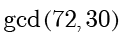 。
。
解:
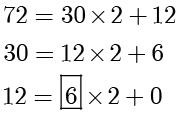
所以
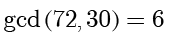 。
。
例
2.3.2
计算
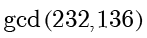 。
。
解:
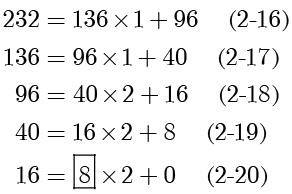
所以
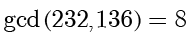 。
。
计算最大公约数的 Python 代码如下,该函数与
math.gcd(a,b)
结果相同。
1 def gcd(a, b):
2 if(b == 0):
3 return abs(a)
4 else:
5 return gcd(b, a % b)
假设
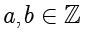 ,
,
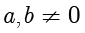 ,如果
,如果
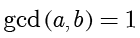 ,那么就可以说
,那么就可以说
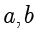 是互素(Coprime)的。
是互素(Coprime)的。
现在设想一个问题,如果给定 3 个整数
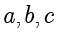 ,需要在方程
,需要在方程
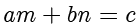 中找到所有的整数
中找到所有的整数
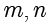 ,应该如何运算呢?该方程也称不定方程或者丢番图方程(Diophantine Equation),值得注意的是,如果
,应该如何运算呢?该方程也称不定方程或者丢番图方程(Diophantine Equation),值得注意的是,如果
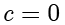 ,则式子被称为齐次的(Homogeneous),反之,则称为非齐次的。
,则式子被称为齐次的(Homogeneous),反之,则称为非齐次的。
首先假设
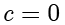 ,那么
,那么
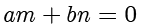 。这个时候需要同除以
。这个时候需要同除以
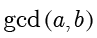 ,得到:
,得到:
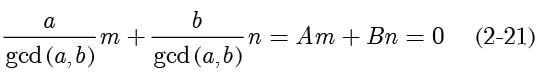
其中
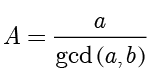 ,
,
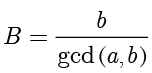 ,此时
,此时
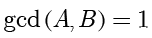 。下一步,可以将
。下一步,可以将
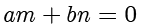 和
和
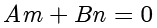 两式联立,得到
两式联立,得到
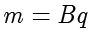 ,
,
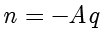 ,
,
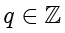 ,有多组解。
,有多组解。
假设
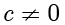 ,同样的,式子左右都同除以
,同样的,式子左右都同除以
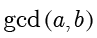 ,得到:
,得到:
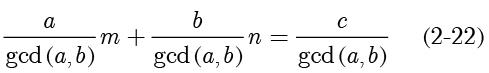
值得注意的是,如果
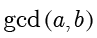 不能整除
不能整除
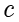 ,那么方程无解。如果可以整除
,那么方程无解。如果可以整除
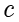 ,那么式子就可以改写成
,那么式子就可以改写成
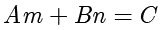 ,
,
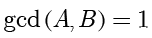 。接着使用欧几里得算法找到方程
。接着使用欧几里得算法找到方程
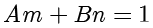 的解
的解
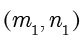 ,方程
,方程
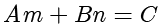 的解
的解
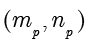 等于
等于
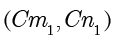 ,方程
,方程
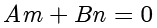 的解
的解
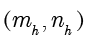 等于
等于
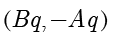 。
。
最后,联立
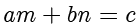 和
和
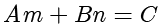 ,得到解:
,得到解:
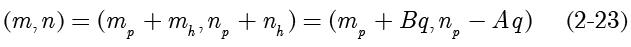
例
2.3.3
找出式
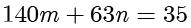 的所有解。
的所有解。
解:
首先使用欧几里得算法计算得到最大公约数
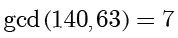 ,发现 7 可以整除 35 ,有解。接着式子同除以
,发现 7 可以整除 35 ,有解。接着式子同除以
 :
:
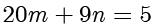
然后对式子
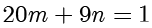 使用欧几里得算法,得到:
使用欧几里得算法,得到:
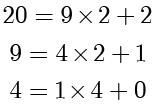
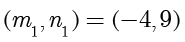 ,
,
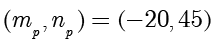 。而
。而
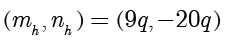 。因此最后得到解
。因此最后得到解
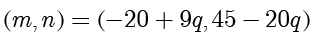 ,其中
,其中
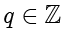 。
。