




除法定理也称带余除法。设
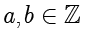 ,且
,且
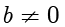 。如果存在
。如果存在
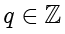 ,使得
,使得
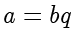 ,则称
,则称
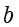 整除
整除
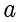 ,记作
,记作
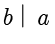 。此时,
。此时,
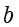 叫作
叫作
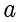 的因数,
的因数,
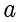 叫作
叫作
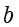 的倍数。
的倍数。
如果
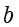 不能整除
不能整除
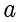 ,则记作
,则记作
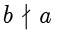 。由于不能整除,这个时候就需要引入余数,即除法定理
[8]
。
。由于不能整除,这个时候就需要引入余数,即除法定理
[8]
。
定理2.2.1 除法定理(Division Theorem)
设
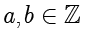 且
且
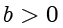 ,这样存在唯一的整数
,这样存在唯一的整数
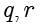 使得:
使得:
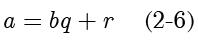
并且
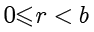 。
。
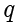 被称为商 (Quotient),
被称为商 (Quotient),
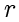 被称为余数 (Remainder)。
被称为余数 (Remainder)。
除法定理是整除的基本定理,是数论的证明中最基本、最常用的工具。例如,在证明与整数不同进制表示相关的定理时,就需要用到除法定理。下面尝试证明除法定理。
证明
设
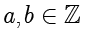 且
且
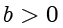 。考虑整数序列:
。考虑整数序列:
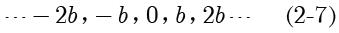
则
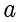 必在上述序列某相邻的两项之间。假设:
必在上述序列某相邻的两项之间。假设:
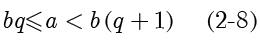
于是
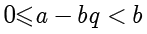 ,令
,令
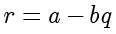 ,则
,则
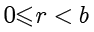 。因此,当
。因此,当
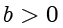 时,就有
时,就有
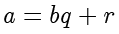 ,证明了
,证明了
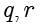 的存在性。
的存在性。
假设存在另一组
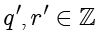 ,使得
,使得
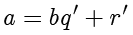 ,
,
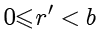 ,则:
,则:
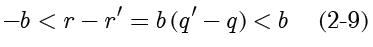
因此
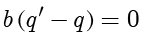 ,从而
,从而
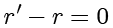 ,即
,即
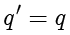 ,
,
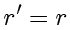 ,证明了
q
,
r
具有唯一性。
,证明了
q
,
r
具有唯一性。
结合存在性和唯一性,除法定理得证。
例
2.2.1
当
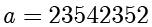 ,
,
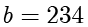 。计算
。计算
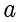 除以
除以
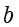 的商和余数。
的商和余数。
解:
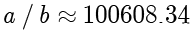 ,那么现在就可以知道商
,那么现在就可以知道商
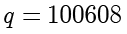 。余数就可以很容易计算得到
。余数就可以很容易计算得到
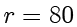 。
。
例
2.2.2
当
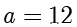 ,
,
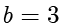 。计算
。计算
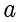 除以
除以
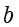 的商和余数。
的商和余数。
解:
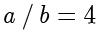 ,那么现在就可以知道商
,那么现在就可以知道商
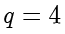 。余数就可以很容易计算得到
。余数就可以很容易计算得到
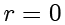 。
。