




什么是集合?读者可以把集合想象成一个盒子,盒子里面装着整数、分数、小数、复数或者字母中的一种或几种,甚至什么都没有。数量也可多可少,没有限制。
定义2.1.1 集合 (Set)
集合指具有某种特定性质的事物的总体。集合中的每个对象叫作这个集合的元素。一般使用
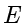 表示集合,
表示集合,
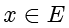 表示元素
表示元素
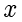 在集合
在集合
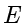 里。
里。
集合具有确定性、无序性、互异性 3 个特征 [8] 。确定性是指如有一个集合和一个元素,那么这个元素只能属于或者不属于该集合,不存在模棱两可的情况; 无序性是指如有两个集合,只要集合中的元素相同,无论如何排序,这两个集合都是相同的;互异性是指对于一个给定的集合,集合中的任何两个元素都是不同的。对于相同、重复的元素,无论多少,只能算作该集合中的一个元素。
集合还可以分为有限集和无限集。下面看一些简单示例。
●
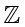 表示所有整数集合,是无限集。
表示所有整数集合,是无限集。
●
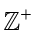 表示正整数集合,是无限集。
表示正整数集合,是无限集。
●
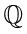 表示有理数集合,是无限集。
表示有理数集合,是无限集。
●
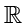 表示实数集合,是无限集。
表示实数集合,是无限集。
●
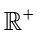 表示正实数集合,是无限集。
表示正实数集合,是无限集。
●
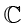 表示复数集合,是无限集。
表示复数集合,是无限集。
●
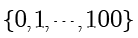 是有限集。
是有限集。
●
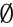 表示空集,是有限集。
表示空集,是有限集。
●
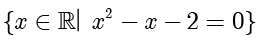 是一个有限集。
是一个有限集。
在密码学中,密钥空间与密文空间是有限的,因此它们都是有限集。为了继续了解什么是集合,还可以将集合分为子集和真子集。
定义2.1.2 子集 (Subset)
如果
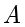 是
是
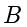 的子集,当且仅当
的子集,当且仅当
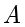 中的每个元素在
中的每个元素在
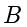 中也会出现。记作
中也会出现。记作
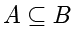 。
。
定义2.1.3 真子集 (Proper Subset)
如果
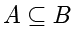 且
且
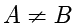 ,则
,则
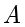 是
是
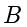 的真子集。记作
的真子集。记作
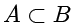 。
。
集合的子集与真子集示例如下。
●
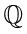 是
是
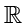 的子集。
的子集。
●
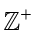 是
是
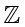 的子集。
的子集。
●
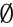 是每一个非空集合的真子集。
是每一个非空集合的真子集。
如果定义两个集合
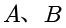 是相等的,则需要满足
是相等的,则需要满足
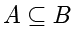 且
且
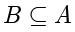 。这样就可以说集合
。这样就可以说集合
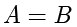 。同时,需要注意区分
。同时,需要注意区分
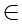 和
和
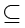 的区别。
的区别。
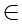 是元素和集合之间的从属关系;
是元素和集合之间的从属关系;
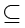 是集合与集合之间的从属关系。它们是不一样的,尽管关系非常紧密。设
是集合与集合之间的从属关系。它们是不一样的,尽管关系非常紧密。设
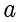 是集合
是集合
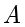 中的一个元素,它们之间的关系可以表示为:
中的一个元素,它们之间的关系可以表示为:
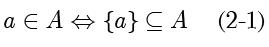
定义2.1.4 交集 (Intersection Set)
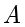 与
与
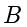 的交集记作
的交集记作
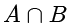 ,定义为:
,定义为:
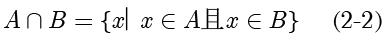
定义2.1.5 并集 (Union Set)
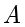 与
与
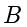 的并集记作
的并集记作
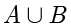 ,定义为:
,定义为:
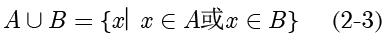
如果元素
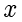 既在集合
既在集合
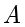 里又在集合
里又在集合
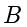 里,那么
里,那么
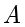 和
和
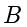 的交集就是
的交集就是
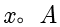 和
和
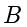 的并集是所有
的并集是所有
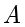 的元素和所有
的元素和所有
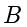 的元素放在一起以后的集合,对于相同的元素,只保留一个。
的元素放在一起以后的集合,对于相同的元素,只保留一个。
例
2.1.1
集合
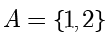 ,集合
,集合
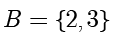 ,求它们的交集和并集。
,求它们的交集和并集。
解:
交集:
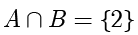
并集:
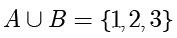
定义2.1.6 差集 (Difference Set)
集合
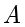 与集合
与集合
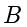 之间不同的部分叫作差集,记作
之间不同的部分叫作差集,记作
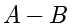 ,定义为:
,定义为:
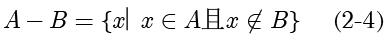
需要注意的是,一般情况下集合之间的相减并不相等,即
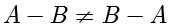 。
。
例
2.1.2
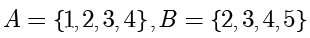 。那么
。那么
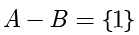 ,
,
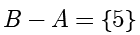 。
。
定义2.1.7 补集 (Complementary Set)
令集合
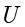 为一个全集合。集合
为一个全集合。集合
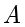 的补集,记作
的补集,记作
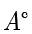 ,定义为:
,定义为:
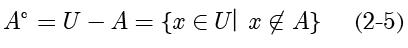
例
2.1.3
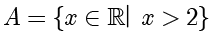 ,则
,则
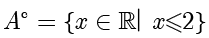 。
。
并集、交集、差集、补集的示意图如图 2-1 所示。
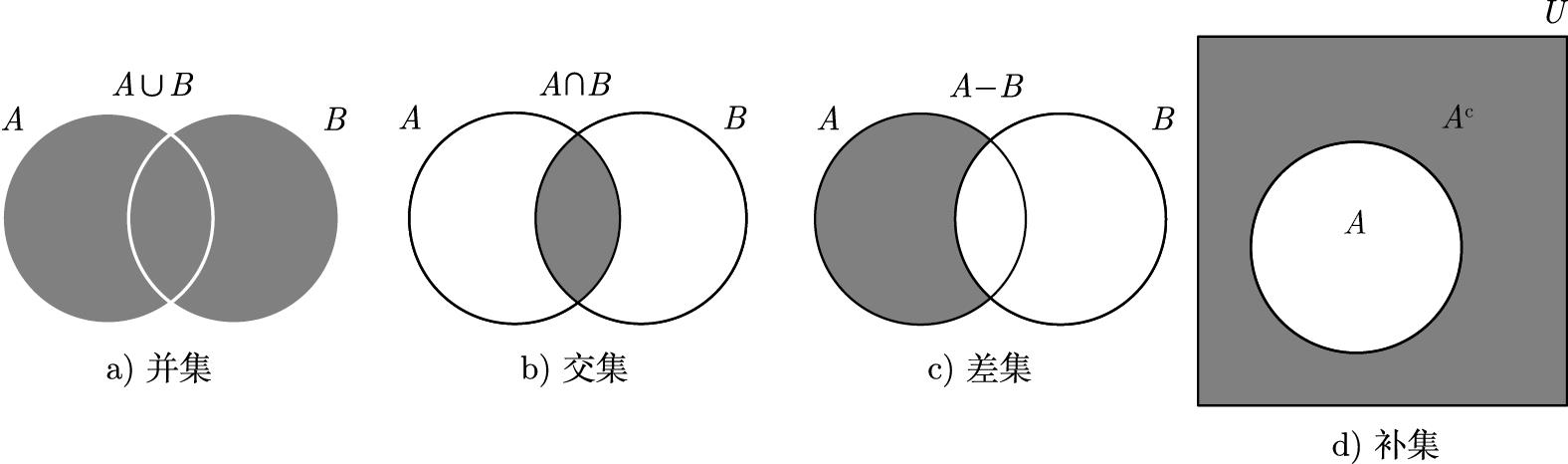
图2-1 集合