五、二次函数之实际问题

例题精析

从地面竖直向上抛出一小球，小球的高度 h （单位： m ）与小球的运动时间 t （单位： s ）之间的关系式是 h ＝30 t -5 t ² （0≤ t ≤6）. 有下列结论：

①小球从抛出到落地需要 6 s ；

②小球运动中的高度可以是 30 m ；

③小球运动 2 s 时的高度小于运动 5 s 时的高度.

其中，正确结论的个数是（ ）

A. 0

B. 1

C. 2

D. 3

解：①令 h ＝0，则 30 t -5 t ² ＝0，

解得 t ₁ ＝0， t ₂ ＝6，

∴小球从抛出到落地需要 6 s ，

故①正确；

② h ＝30 t -5 t ² ＝-5（ t ² -6 t ）＝-5（ t -3） ² +45，

∵-5＜0，

∴当 t ＝3 时， h 有最大值，最大值为 45，

∴小球运动中的高度可以是 30 m ，

故②正确；

③ t ＝2 时， h ＝30×2-5×4＝40（ m ），

t ＝5 时， h ＝30×5-5×25＝25（ m ），

∴小球运动 2 s 时的高度大于运动 5 s 时的高度，

故③错误.

故选： C .

精析一

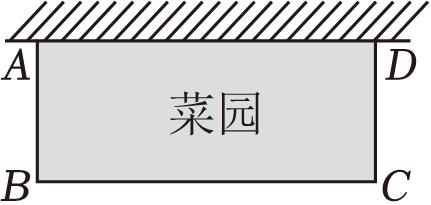
如图，要围一个矩形菜园 ABCD ，其中一边 AD 是墙，且 AD 的长不能超过 26 m ，其余的三边 AB ， BC ， CD 用篱笆，且这三边的和为 40 m ，有下列结论：① AB 的长可以为 6 m ；② AB 的长有两个不同的值满足菜园 ABCD 面积为 192 m ² ；③菜园 ABCD 面积的最大值为 200 m ² . 其中，正确结论的个数是（ ）

A. 0

B. 1

C. 2

D. 3

精析二

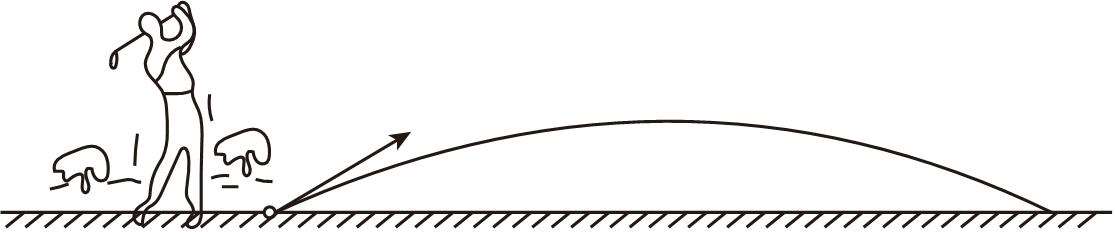
如图，以某速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线将是一条抛物线. 如果不考虑空气阻力，小球在 4 s 时落地，小球的飞行高度 h （单位： m ）与飞行时间 t （单位： s ）之间具有函数关系 h ＝ at ² +20 t （ a 为常数， a ≠0）. 有下列结论：

① a 值为-5；②小球的飞行高度最高可达到 21 m ；

③小球有两个飞行的时间使小球的高度刚好达到 15 m . 其中，正确结论的个数是（ ）

A. 0

B. 1

C. 2

D. 3

精析三

某商品现在的售价为每件 60 元，每星期可卖出 300 件，市场调查反映：如调整价格，每涨价 1 元，每星期要少卖出 10 件；每降价 1 元，每星期可多卖出 20件，已知商品的进价为每件 40 元，有下列结论：

①设每件涨价 x 元，则实际卖出（300-10 x ）件；

②在降价的情况下，降价 5 元，即定价 55 元时，利润最大，最大利润是 6250元；

③综合涨价与降价两种情况及现在的销售状况可知，定价 57.5 元时利润最大；其中，正确结论的个数是（ ）

A. 0 个

B. 1 个

C. 2 个

D. 3 个 tXFXT0qEKZPF44FA72Tk0sIw8HDkRpS86vDv1c8P/FNxrh08HjXCZtouLJxujf39