




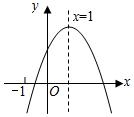
已知二次函数 y = ax 2 + bx + c ( a ≠0)的图象如图所示,有下列 5 个结论:
① abc >0;
② b 2 <4 ac ;
③2 c <3 b ;
④ a +2 b > m ( am + b )( m ≠1);
⑤若方程| ax 2 + bx + c |=1 有四个根,则这四个根的和为 2,
其中正确的结论有( )
A. 2 个
B. 3 个
C. 4 个
D. 5 个
解:∵抛物线开口向下,
∴ a <0,
∵抛物线对称轴为直线
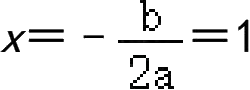 ,
,
∴ b =-2 a >0,
∵抛物线与 y 轴交点在 x 轴上方,
∴ c >0,
∴ abc <0,①错误.
∵抛物线与 x 轴有 2 个交点,
∴Δ= b 2 -4 ac >0,
∴ b 2 >4 ac ,②错误.
∵ x =-1 时, y <0,
∴ a - b + c <0,
∵ b =-2 a ,
∴
a
=-
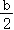 ,
,
∴-
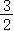 b
+
c
<0,
b
+
c
<0,
∴2 c <3 b ,③正确.
∵ x =1 时, y = a + b + c 为函数最大值,
∴ a + b + c > m ( am + b )+ c ( m ≠1),
∴ a + b > m ( am + b )( m ≠1),
∵ b >0,
∴ a +2 b > a + b > m ( am + b )( m ≠1),④正确.
方程| ax 2 + bx + c |=1 的四个根分别为 ax 2 + bx + c =1 和 ax 2 + bx + c =-1 的根,
∵抛物线 y = ax 2 + bx + c 关于直线 x =1 对称,
∴抛物线与直线 y =1 的交点的横坐标为之和为 2,
抛物线与直线 y =-1 的交点横坐标为之和为 2,
∴方程| ax 2 + bx + c |=1 的四个根的和为 4,⑤错误.
故选: A .
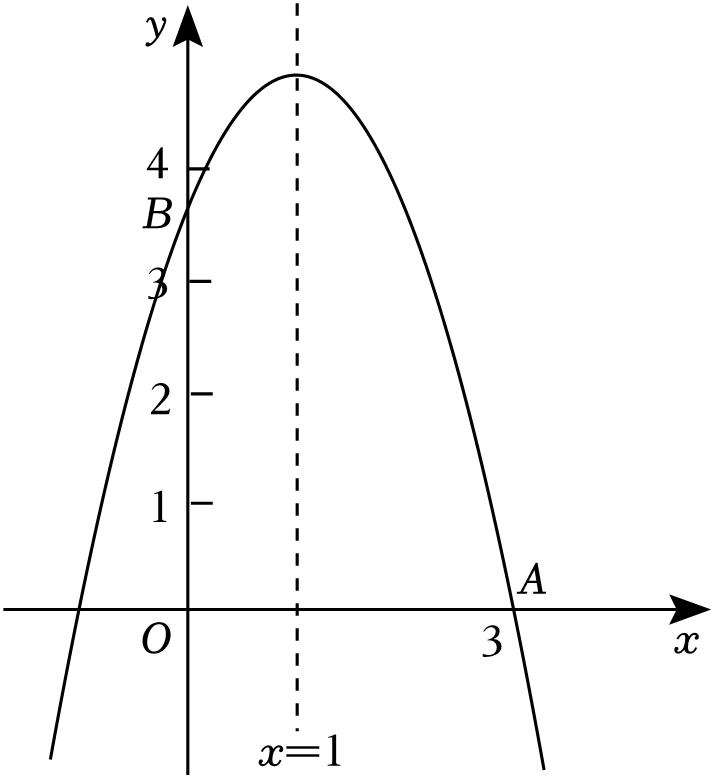
如图,二次函数
y
=
ax
2
+
bx
+
c
(
a
≠0)的图象与
x
轴交于点
A
(3,0),与
y
轴的交点
B
在(0,3)与(0,4)之间(不包括这两点),对称轴为直线
x
=1. 下列结论:①
abc
<0;②
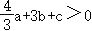 ;③
;③
 ;④若
x
1
,
x
2
(
x
1
<
x
2
)是方程
ax
2
+
bx
+
c
=
m
(
m
<0)的两个根,则有
x
1
<-1<3<
x
2
. 其中正确结论的个数是( )
;④若
x
1
,
x
2
(
x
1
<
x
2
)是方程
ax
2
+
bx
+
c
=
m
(
m
<0)的两个根,则有
x
1
<-1<3<
x
2
. 其中正确结论的个数是( )
A. 1 个
B. 2 个
C. 3 个
已知二次函数 y = ax 2 + bx + c ( a >0)的图象与 x 轴负半轴交于 A , B 两点,与 y 轴的正半轴交于点 C ,它的对称轴为直线 x =-1,有下列结论:① abc <0;② c - a >0;③当 x =- k 2 -2( k 为任意实数)时, y ≥ c ;④若 x 1 , x 2 ( x 1 < x 2 )是方程 ax 2 + bx + c =0 的两根,则方程 a ( x - x 1 )( x - x 2 )-1=0 的两根 m , n ( m < n )满足 m < x 1 且 n > x 2 ;其中,正确结论的个数是( )
A. 1 个
B. 2 个
C. 3 个
D. 4 个
已知二次函数 y = ax 2 + bx + c = a ( x +2)( x - t )( a 为非零常数,1< t <2),图象与 y 轴负半轴的交点在点(0,-2)的上方,有下列结论:
① a > b >0;
②关于 x 的方程 ax 2 +( b -1) x + c +2=0 有两个不相等的实数根;
③2 a - b -1<0.
其中,正确结论的个数是( )
A. 3
B. 2
C. 1
D. 0