




二次函数
y
=
ax
2
+
bx
+
c
(
a
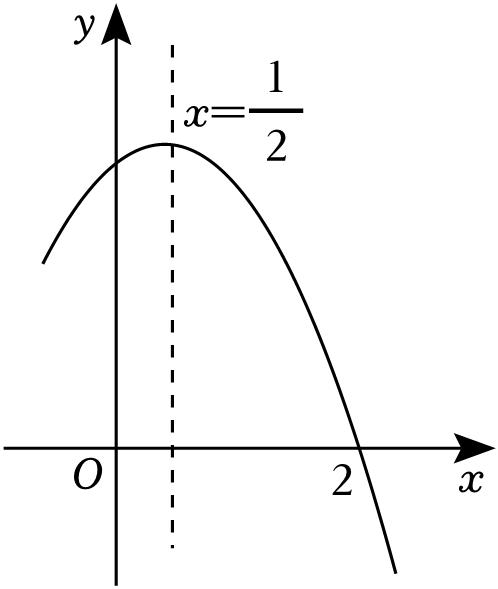
≠0)的部分图象如图所示,对称轴为直线
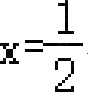 且经过点(2,0). 下列说法:①
abc
<0;②-2
b
+
c
=0;③4
a
+2
b
+
c
<0;④若
且经过点(2,0). 下列说法:①
abc
<0;②-2
b
+
c
=0;③4
a
+2
b
+
c
<0;④若
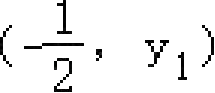 ,
,
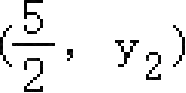 是抛物线上的两点,则
y
1
<
y
2
;
是抛物线上的两点,则
y
1
<
y
2
;
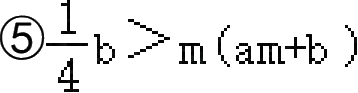 (其中
(其中
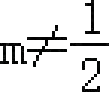 )其中正确的结论有( )
)其中正确的结论有( )
A. 2
B. 3
C. 4
D. 5
解:∵抛物线的开口向下,与 y 轴的交点位于 y 轴正半轴,
∴ a <0, c >0,
∵抛物线的对称轴为
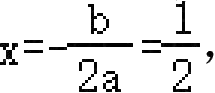
∴ b =- a >0,
∴ abc <0,则结论①正确;
将点(2,0)代入二次函数的解析式得:4 a +2 b + c =0,则结论③错误;
将 a =- b 代入 4 a +2 b + c =0 得:-2 b + c =0,则结论②正确;
∵抛物线的对称轴为
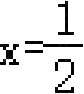 ,
,
∴
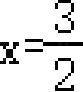 和
和
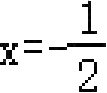 时的函数值相等,即都为
y
1
,
时的函数值相等,即都为
y
1
,
又∵当
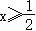 时,
y
随
x
的增大而减小,且
时,
y
随
x
的增大而减小,且
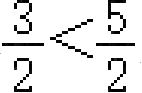 ,
,
∴ y 1 > y 2 ,则结论④错误;
由函数图象可知,当
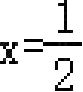 时,
y
取得最大值,最大值为
时,
y
取得最大值,最大值为
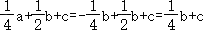 ,
,
∵
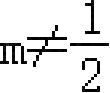 ,
,
∴
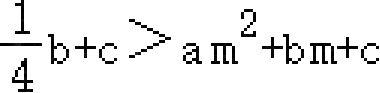 ,即
,即
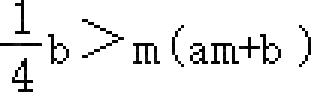 ,结论⑤正确;
,结论⑤正确;
综上,正确的结论有①②⑤,共 3 个.
故选: B .
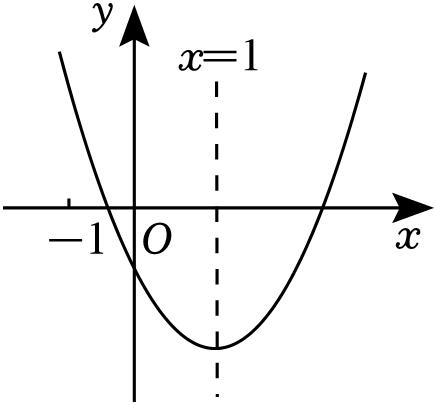
二次函数
y
=
ax
2
+
bx
+
c
(
a
≠0)的图象如图所示,它的对称轴为直线
x
=1,则下列结论:①
abc
<0;②当
x
>2 时,
y
>0;③
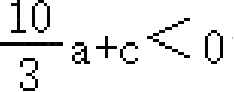 ;④
a
+
b
≤
m
(
am
+
b
)(
m
为任意实数);其中正确结论的个数是( )
;④
a
+
b
≤
m
(
am
+
b
)(
m
为任意实数);其中正确结论的个数是( )
A. 1 个
B. 2 个
C. 3 个
D. 4 个
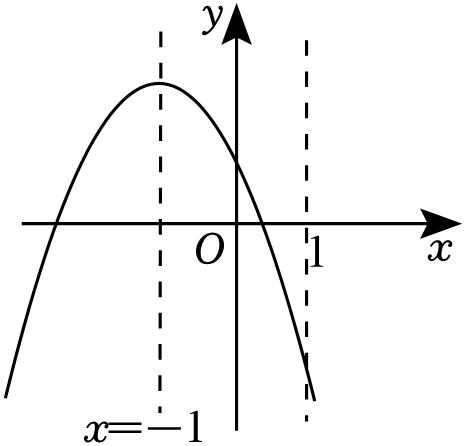
二次函数 y = ax 2 + bx + c ( a ≠0)的图象如图所示,下列结论:① abc >0;② b 2 -4 ac <0;③4 a + c >2 b ;④( a + c ) 2 > b 2 ;⑤ x ( ax + b )≤ a - b ,其中正确的结论是( )
A. ①③④
B. ①③⑤
C. ②③④
D. ①③④⑤
已知抛物线 y = ax 2 + bx + c ( a 、 b 、 c 为常数,且 a >0 的对称轴为直线 x =1,与 x 轴的一个交点( x 0 ,0)满足-1< x 0 <0),现有结论:① abc <0,② b 2 >4 ac ,③3 a + c >0,④ ac - bc + c 2 <0. 其中结论正确的有( )
A. 1 个
B. 2 个
C. 3 个
D. 4 个