下载掌阅APP，畅读海量书库
立即打开
二次函数图像及性质、二次函数的实际问题，一般在天津中考12 题出现。因为近几年中考，选择有个很严重的漏洞，有规律，3 A 3 B 3 C 3 D，导致很多同学基本不看 12 题，直接根据前十一道题的答案，推算出最后一题的答案，所以基本上很多同学都不愿意听老师们对这道题的讲解，更不用说去分析了，好消息是 2024 年这个规律打破，打破之后就要求同学们会对这道题进行分析，那进行分析的前提，就需要前期对基础知识点的掌握，也对后续各位同学去解 25 题提供帮助，随着 23 年对 12 题的改革，从原来对二次函数图像性质的分析改成了二次函数的实际应用，实际上是降低了 12 题的难度，但是对于大部分同学来说，因为对于此题的忽略，怎么换也是难。
在这给各位同学提出一些要求，既然选择了这本书进行学习，希望各位能静下心，学习二次函数章节，这个非常重要，不仅仅是针对12 题，同时也针对了 25 题，也可以和一元二次方程相结合，为日后高中的学习也会打下坚实的基础，所以，想要冲击高分，相信各位可以迈出这坚实的一步！
1.a决定开口方向。
①a>0，开口向上。
②a<0，开口向下。
2.c决定与y轴的交点位置。
①c>0，交于y轴正半轴。
②c<0，交于y轴负半轴。
3.a.b决定对称轴与y轴的位置关系。（对称轴x=
）
总结：①对称抽在y轴右侧，a.b异号。
②对称轴在y轴左侧，a.b同号。
记忆口诀：“左同右异”。
已知对称轴，即可求出a与b的等量关系。
4.a.b.c决定最值或与x轴的交点个数。
最值：
顶点坐标
①a>0，取最小值。
②a<0，取最大值。
判别式：△=b 2 -4ac>0
①b 2 -4ac>0，与x轴有两个交点。
②b 2 -4ac=0，与x轴有一个交点。
③b 2 -4ac<0，与x轴无交点。
5.常见的三种解析式。
①y=ax 2 +bx+c（一般式）（已知任意三点A.B.C）
②y=a(x-h) 2 +k（顶点式）（已知顶点坐标A和另一点B）
③y=a(x-x 1 )(x-x 2 )（交点式）（已知三点A.B.C。注：有两点特殊 A =( x 1 ,0)， B =( x 2 ,0)）
二次函数
y
＝
ax
2
+
bx
+
c
（
a
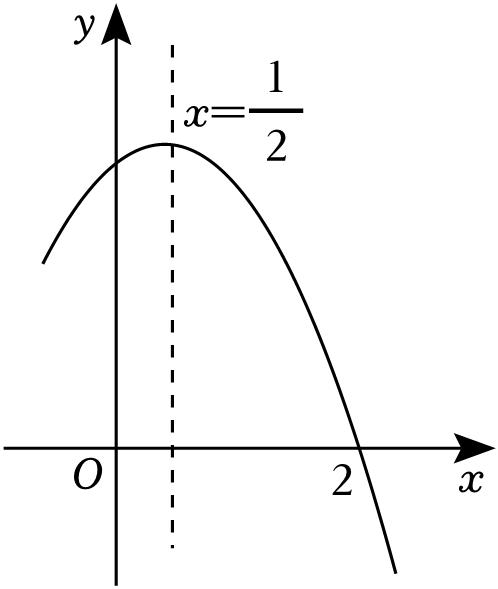
≠0）的部分图象如图所示，对称轴为直线
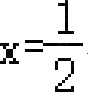且经过点（2，0）. 下列说法：①
abc
＜0；②-2
b
+
c
＝0；③4
a
+2
b
+
c
＜0；④若
，
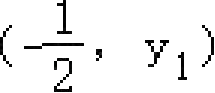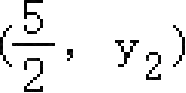是抛物线上的两点，则
y
1
＜
y
2
；
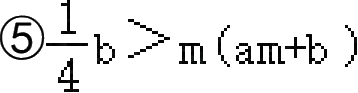（其中
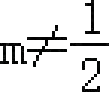）其中正确的结论有（ ）
A. 2
B. 3
C. 4
D. 5
解：∵抛物线的开口向下，与 y 轴的交点位于 y 轴正半轴，
∴ a ＜0， c ＞0，
∵抛物线的对称轴为
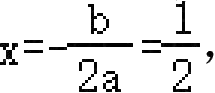
∴ b ＝- a ＞0，
∴ abc ＜0，则结论①正确；
将点（2，0）代入二次函数的解析式得：4 a +2 b + c ＝0，则结论③错误；
将 a ＝- b 代入 4 a +2 b + c ＝0 得：-2 b + c ＝0，则结论②正确；
∵抛物线的对称轴为
，
∴
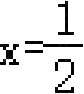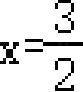和
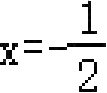时的函数值相等，即都为
y
1
，
又∵当
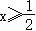时，
y
随
x
的增大而减小，且
，
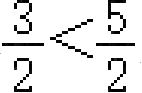∴ y 1 ＞ y 2 ，则结论④错误；
由函数图象可知，当
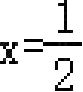时，
y
取得最大值，最大值为
，
∵
，
∴
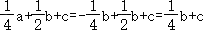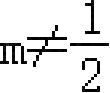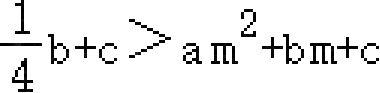，即
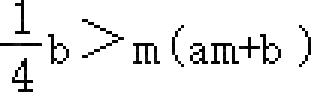，结论⑤正确；
综上，正确的结论有①②⑤，共 3 个.
故选： B .
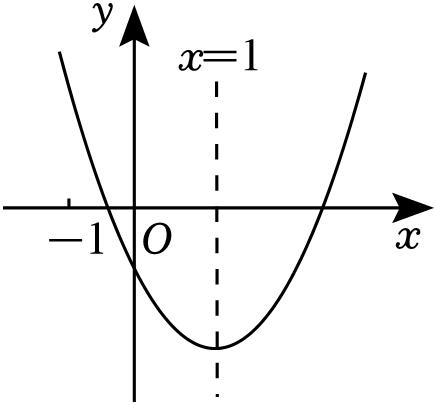
二次函数
y
＝
ax
2
+
bx
+
c
（
a
≠0）的图象如图所示，它的对称轴为直线
x
＝1，则下列结论：①
abc
＜0；②当
x
＞2 时，
y
＞0；③
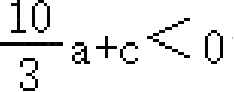；④
a
+
b
≤
m
（
am
+
b
）（
m
为任意实数）；其中正确结论的个数是（ ）
A. 1 个
B. 2 个
C. 3 个
D. 4 个
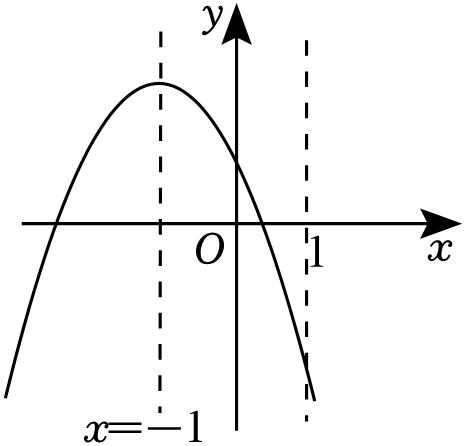
二次函数 y ＝ ax 2 + bx + c （ a ≠0）的图象如图所示，下列结论：① abc ＞0；② b 2 -4 ac ＜0；③4 a + c ＞2 b ；④（ a + c ） 2 ＞ b 2 ；⑤ x （ ax + b ）≤ a - b ，其中正确的结论是（ ）
A. ①③④
B. ①③⑤
C. ②③④
D. ①③④⑤
已知抛物线 y ＝ ax 2 + bx + c （ a 、 b 、 c 为常数，且 a ＞0 的对称轴为直线 x ＝1，与 x 轴的一个交点（ x 0 ，0）满足-1＜ x 0 ＜0），现有结论：① abc ＜0，② b 2 ＞4 ac ，③3 a + c ＞0，④ ac - bc + c 2 ＜0. 其中结论正确的有（ ）
A. 1 个
B. 2 个
C. 3 个
D. 4 个