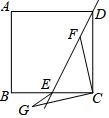
四线共点,两两相等,夹角相等.
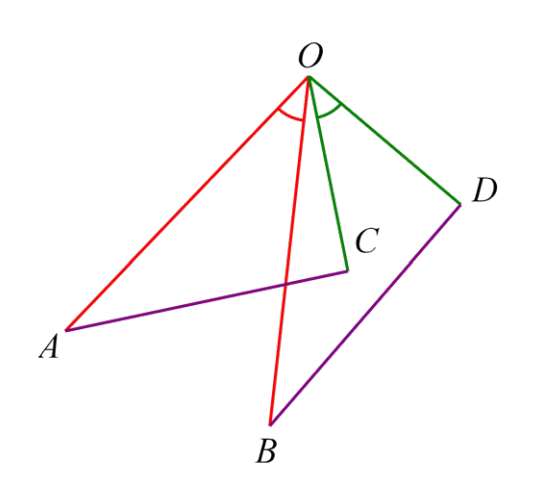
条件:如图, OA = OB , OC = OD (四线共点,两两相等),∠ AOB =∠ COD (夹角相等)
结论:△ OAC ≌△ OBD ( SAS )
常见的等边三角形和正方形.
(1)如图, B 、 C 、 D 三点共线,△ ABC 和△ CDE 是等边三角形,连接 AD 、 BE ,交于点 P :
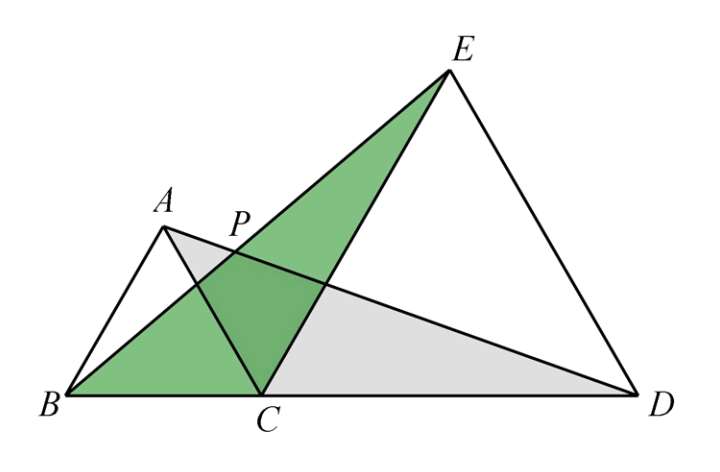
结论一:△ ACD ≌△ BCE
证明:
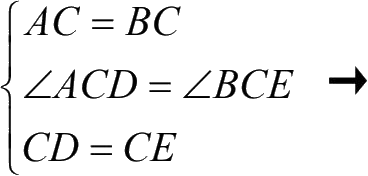 △
ACD
≌△
BCE
(
SAS
)
△
ACD
≌△
BCE
(
SAS
)
(2)记 AC 、 BE 交点为 M , AD 、 CE 交点为 N :
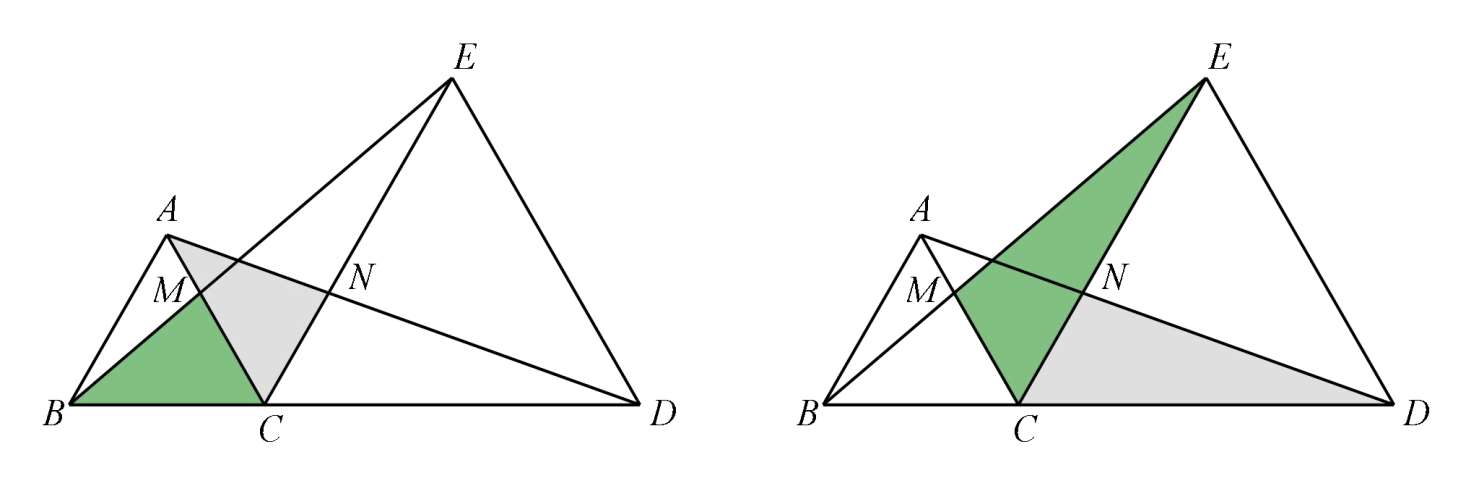
结论二:△ ACN ≌△ BCM ;△ MCE ≌△ NCD
证明:
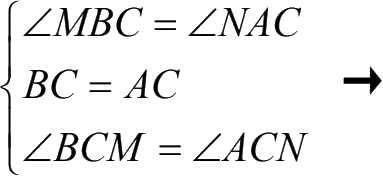 △
ACN
≌△
BCM
(
SAS
);
△
ACN
≌△
BCM
(
SAS
);
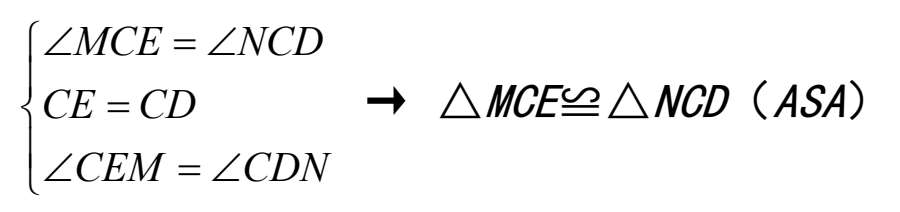
(3)连接 MN :
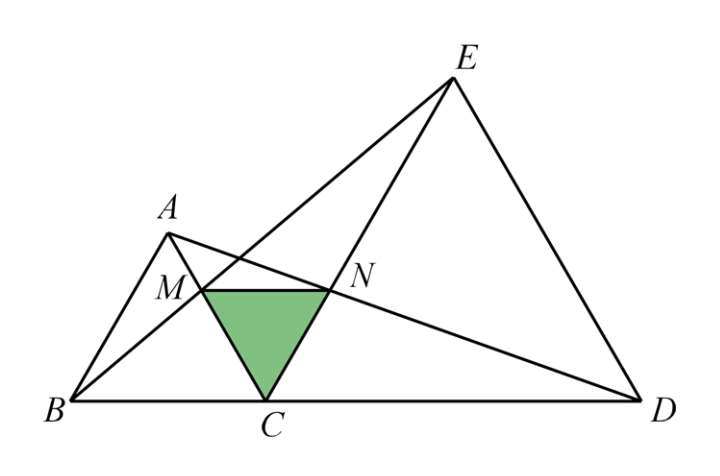
结论三:△ MNC 是等边三角形.
证明:
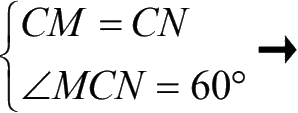 △
MCN
是等边三角形.
△
MCN
是等边三角形.
(4)记 AD 、 BE 交点为 P ,连接 PC :
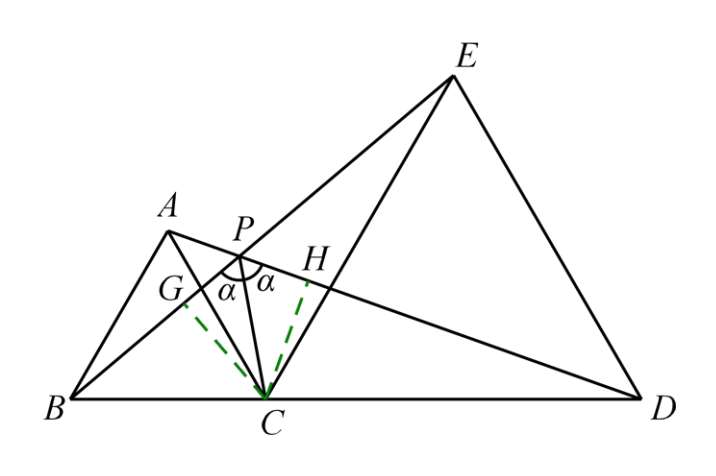
结论四: PC 平分∠ BPD
证明:△ BCE ≌△ ACD → CG = CH → PC 平分∠ BPD .
(5)结论五:∠ APB =∠ BPC =∠ CPD =∠ DPE =60°.
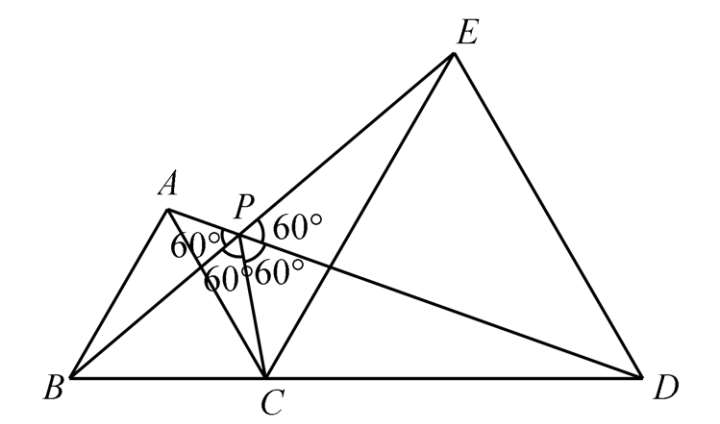
(6)连接 AE :
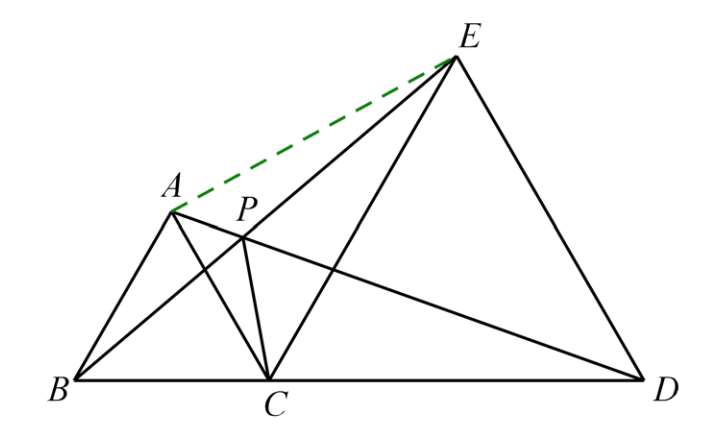
结论六: P 点是△ ACE 的费马点( PA + PC + PE 值最小)
如图,四边形 ABCD 和四边形 CEFG 均为正方形,连接 BE 、 DG :
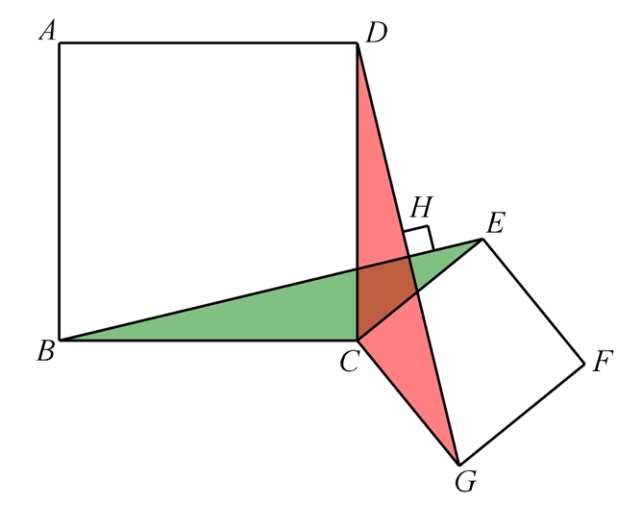
结论一:△ BCE ≌△ DCG
证明:
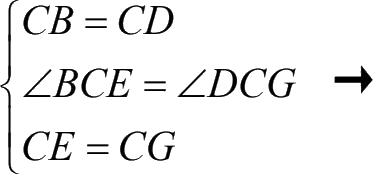 △
BCE
≌△
DCG
(
SAS
)
△
BCE
≌△
DCG
(
SAS
)
结论二: BE = DG , BE ⊥ DG
证明:△ BCE ≌△ DCG → BE = DG ;
∠ CBE =∠ CDG →∠ DHB =∠ BCD =90°(旋转角都相等)
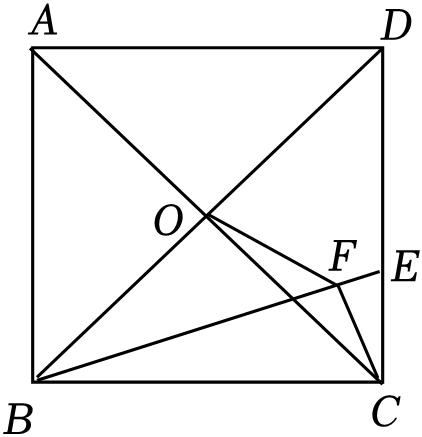
如图,正方形
ABCD
的边长是
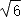 ,对角线的交点为
O
,点
E
在边
CD
上且
CE
=
,对角线的交点为
O
,点
E
在边
CD
上且
CE
=
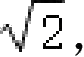 CF
⊥
BE
,连接
OF
,则
OF
=____________.
CF
⊥
BE
,连接
OF
,则
OF
=____________.
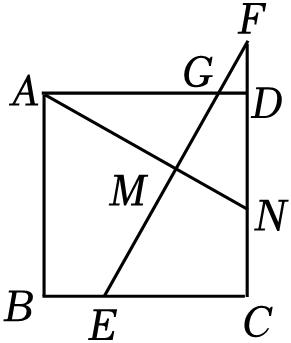
如图,在正方形 ABCD 中,点 F 在边 CD 的延长线上,点 E 是边 BC 上的一点,且 BE = DF ,连接 EF 交边 AD 于点 G . 过点 A 作 AN ⊥ EF ,垂足为点 M ,交边 CD 于点 N . 若 BE =5, CN =8,则线段 AN 的长为____________.
如图,四边形 ABCD 是边长为 2 的正方形, E 是 BC 边的中点, F 是直线 DE 上的动点. 连接 CF ,将线段 CF 逆时针旋转 90°得到 CG ,连接 EG ,则 EG 的最小值是____________.