下载掌阅APP，畅读海量书库
立即打开
加密方法是指使用算法和密钥加密信息的方法，加密体制是指通过采用适当的加密方法使通信双方能在不安全的信道上进行信息的秘密交换。一种加密体制由使用适当的密钥把明文转换成密文的过程和它的反过程组成，密钥是完成转换的基本因素。
基于共享密钥的加密方法又称为对称密钥加密方法，对称密码学的基本思想就是密钥共享。用户Alice和Bob相互通信，采用双方共享的密钥和对称密钥加密方法保护消息，攻击者即使截获密文，也会因为没有适当的密钥不能得到任何关于通信内容的有效信息。通常使用流密码（Stream Cipher）和分组密码（Block Cipher）实现对称密钥加密。
1.流密码
设 K 为密钥的集合， M 为明文的集合。一个流密码
E * ： M * × K * → C * ， E * ( k , m )= c = c 1 c 2 c 3 …
利用密钥流 k = k 1 k 2 k 3 …∈ K * （ k i ∈ K ）把明文序列 m = m 1 m 2 m 3 …∈ M * （ m i ∈ M ）加密为密文序列 c = c 1 c 2 c 3 …∈ C * （ c i ∈ C ）。因此，存在加密映射
E k ： M → C
使得对任意的密钥
k
，有
，
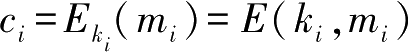i
=1，2，…。流密码加密通信的流程图如图3-4所示。
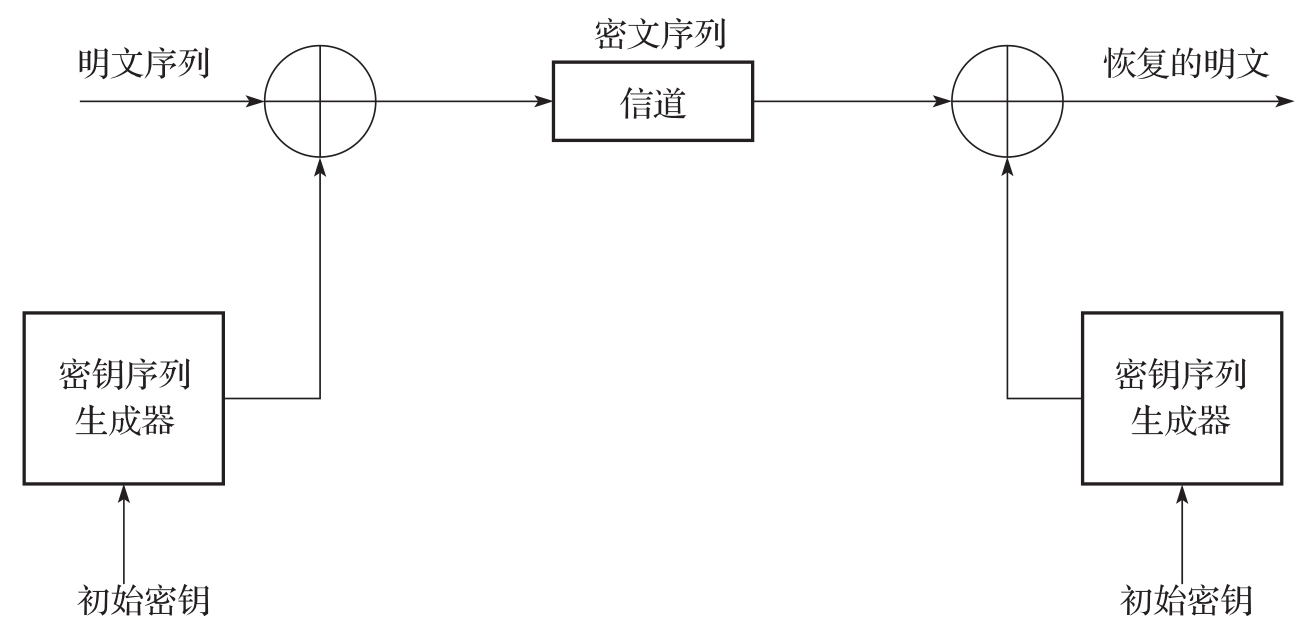
图3-4 流密码加密通信流程图
流密码又称序列密码，是对称密码学中的重要体制之一，它的起源可以追溯到20世纪20年代的Vernam密码。Vernam密码简单且易于实现，Vernam密码的关键是生成随机的密钥序列。设 M = K = C ={0,1}，并且
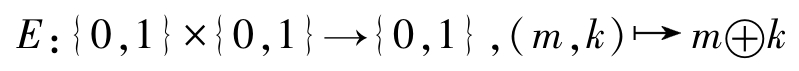
是消息比特和密钥比特的简单异或运算。为了加密消息， m = m 1 m 2 m 3 …需要一个密钥流 k = k 1 k 2 k 3 …， k i ∈{0,1}。
加密函数定义如下：
E * （ k，m ）= c = c 1 c 2 c 3 …，其中 c i = m i ⊕ k i
解密函数定义如下：
D * （ k，c ）= m = m 1 m 2 m 3 …，其中 m i = c i ⊕ k i
例3-4 流密码应用示例
流密码是一种方便快捷的加密方法，在现实中得到了广泛的应用。RC4密码是目前普遍使用的流密码之一，是美国麻省理工学院的Ron Rivest于1987年设计的密钥长度可变的流密码算法。RC4密码不仅已应用于Microsoft Windows和Lotus Notes等应用程序中，而且已应用于安全套接层（Secure Sockets Layer，SSL）保护因特网的信息流，还应用于无线局域网通信协议WEP（Wired Equivalent Privacy）以及蜂窝数字数据包规范中。祖冲之序列密码算法是中国自主研发的流密码算法，是运用于移动通信4G网络中的国际标准密码算法，该算法包括祖冲之算法、加密算法（128-EEA3）和完整性算法（128-EIA3）三个部分。被国际组织3GPP推荐为4G无线通信的第三套国际加密和完整性标准的候选算法。
2.分组密码
分组密码是将明文分成一些固定长度的段落（分组），在密钥作用下逐段进行加密的方法，这样做的好处是处理速度快、可靠性高、软（硬）件都能实现，而且节省资源、容易标准化。因此，分组密码得到了广泛的应用，同时也成为许多密码组件[比如MAC（消息认证码）系统]的基础。
分组密码满足 M = C ={0,1} n ， n 称为密码的分组长度。这是一个二元分组密码的概念，一般地，码元不限于二元，且 M 和 C 的长度不一定相等。对于密钥 k ，加密函数 E 是{0,1} n 上的一个置换，消息空间由分组长度为 n 的2 n 个明文消息构成。分组密码的加密原理是：将明文按照某一规定的 n 比特长度分组，最后一组长度不够时要用规定的值填充，使其成为完整的一组，然后使用相同的密钥对每一分组分别进行加密。典型的分组加密方法有DES、三重DES、AES和IDEA，以及国密算法SM1、SM4和SM7。
（1）DES
1973年美国国家标准局（National Bureau of Standards,NBS）公开征集用于保护商用信息的密码算法，并于1975年公布了数据加密标准（Data Encryption Standard，DES）。随后人们陆续设计了许多成熟的分组密码算法，如IDEA、SAFER、Skipjack、RC5、Blowfish、Rijndael等。分组密码的核心问题就是设计足够复杂的算法，以实现香农提出的混乱和扩散准则。DES是最著名的、使用最广泛的对称密钥分组加密算法。1977年1月15日，美国联邦信息处理标准版46（FIPS PUB 46）中给出了DES的完整描述。DES算法首开先例成为第一代公开的、完全说明实现细节的商业级密码算法，并被世界公认。
DES处理 n =64比特的明文分组并产生64比特的密文分组（如图3-5所示）。密钥的有效长度为56比特，更准确地说，输入密钥为64比特，其中8比特（8,16,…,64）可用作校验位。
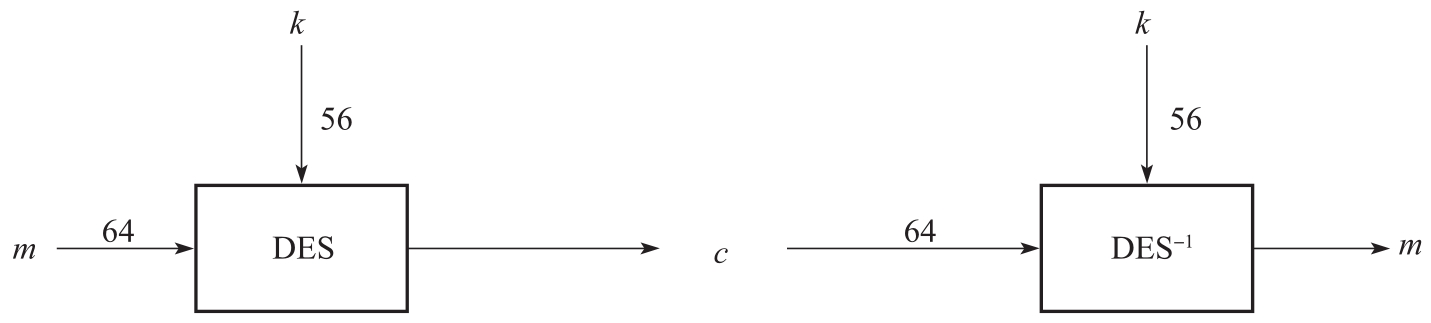
图3-5 DES工作原理图
DES算法由一个映射
DES：{0,1} 64 ×{0,1} 56 →{0,1} 64
构成，若选好密钥 k ，则有
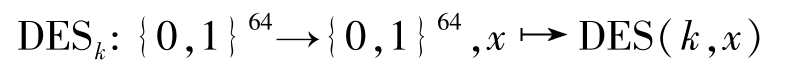
DES加密过程要经过16圈迭代，从56比特的有效密钥生成16个子密钥{ k 1 ，…， k 16 }，每个子密钥 k i 的长度是48比特，在16圈迭代中使用。解密和加密采用相同的算法，并且所使用的密钥也相同，只是各个子密钥的使用顺序不同（如图3-6所示）。
在图3-6的DES算法描述中，64比特明文经过初始置换（Initial Permutation）IP后，分成左半部和右半部两块，每块32比特，进入16圈迭代。在DES的16圈迭代中，映射
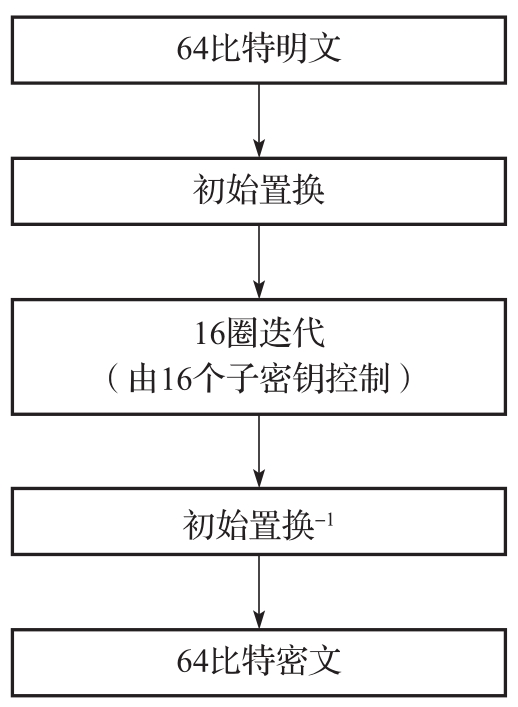
图3-6 DES算法框图
f ：{0,1} 32 ×{0,1} 48 →{0,1} 32
是建立分组的基础之一。 f 取决于32比特的明文和48比特的密钥，它由一个替换 S 和一个置换 P 构成：
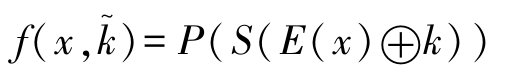
32比特的明文 x 经
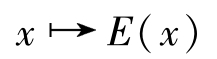
扩展为48比特，并将其与48比特的密钥
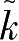异或，然后把所得的48比特分成8组，每组6比特。用
S
将每组替换为4比特，最后对得到的32比特（即8组×4比特）进行
P
置换。对于每一个子密钥
k
i
，可得
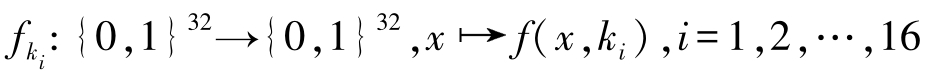
对于 i =1,2,…,16中的每一轮迭代，对左半部32比特明文 x 和右半部32比特明文 y 的加密密文 f i ( y ）进行异或，可得
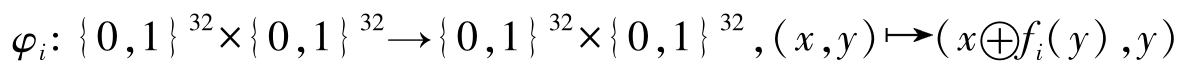
函数DES k 由 φ 1 ,…, φ 16 及
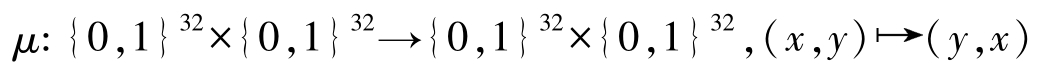
组合而成，即
DES k :{0,1} 64 →{0,1} 64
DES k ( x )=IP -1 ° φ 16 ° μ °… μ ° φ 2 ° μ ° φ 1 °IP( x )
其中IP是公开的已知置换，符号“°”表示组合操作。
由于
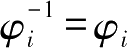及
μ
-1
=
μ
，因此，对所有的明文消息
x
∈{0，1}
64
，恒有
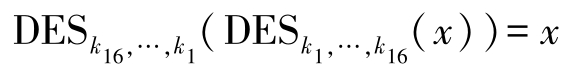
DES使用16个不同的密钥通过16轮相同类型的加密而得到密文，其中，16个密钥是由56比特的初始密钥生成的， φ i 称为第 i 轮加密函数，除最后一轮之外，每一轮加密后左半部和右半部都互换。DES算法的密码强度取决于 f 的设计，特别是8个著名的处理替换的S盒的设计。
例3-5 DES加密示例
设明文 m =“computer”，密钥 k =“program”，相应ASCII码用二进制表示为：
m =01100011 01101111 01101101 01110000
01110101 01110100 01100101 01110010
k =01110000 01110010 01101111 01100111
01110010 01100001 01101101
因为 k 只有56比特，所以必须在第8、16、24、32、40、48、56、64位插入奇偶校验位，合成64比特。当然，这8位对加密过程没有影响。
m 经过初始置换得到：
L 0 =11111111 10111000 01110110 01010111
R 0 =00000000 11111111 00000110 10000011
k 经过子密钥生成过程得到第1轮48位子密钥：
k 1 =00111101 10001111 11001101 00110111 00111111 00000110
m 经过16轮迭代，再经过逆初始置换，得到密文：
c =0xb2dcc3be594c571d
相应二进制表示为：
c =10110010 11011100 11000011 10111110
01011001 01001100 01010111 00011101
（2）三重DES
三重DES（记为3DES）加密算法是一种改进的DES算法，它使用3组密钥 k 1 、 k 2 和 k 3 对同一组明文进行多重加密（如图3-7所示），密钥长度为168比特（即56比特×3）。
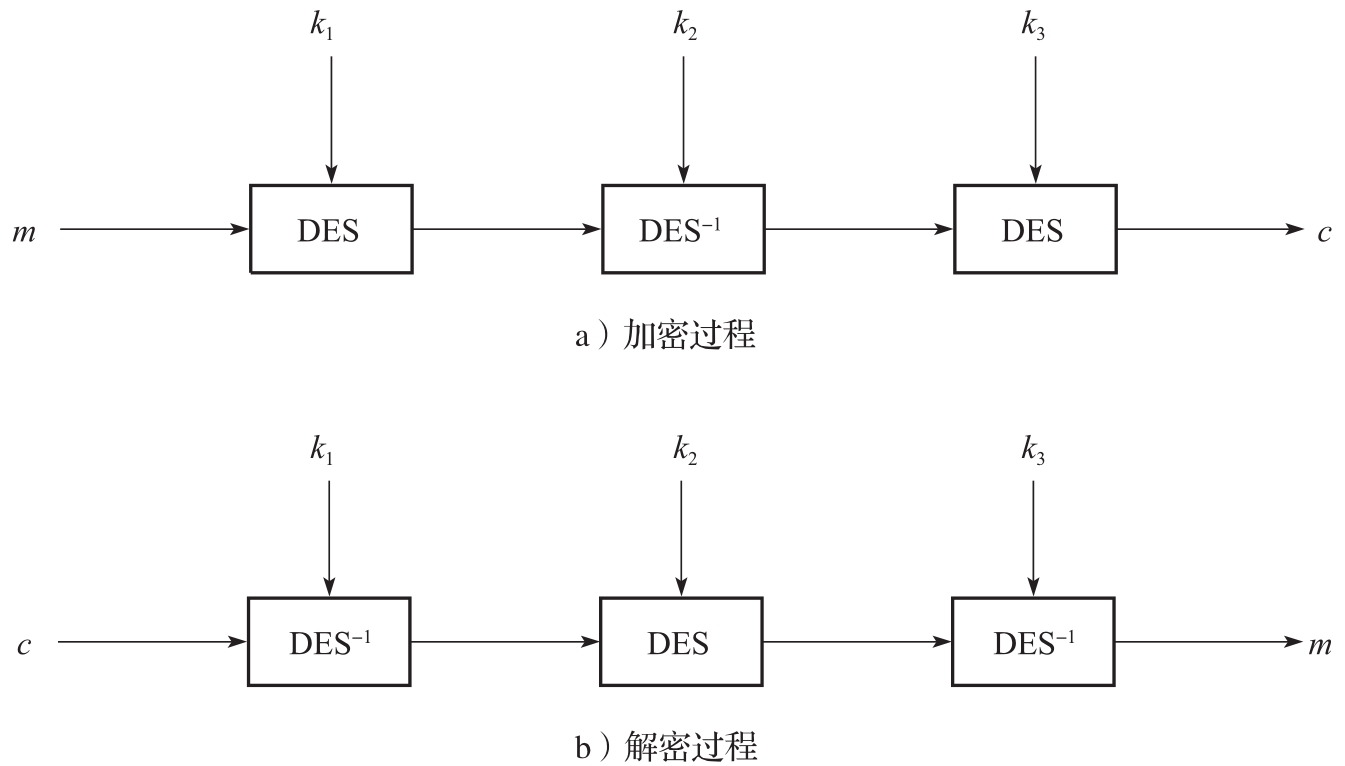
图3-7 三重DES工作原理图
加密算法定义如下：
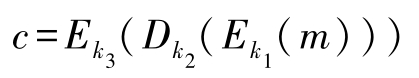
解密算法定义如下：
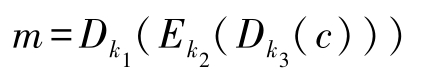
在DES的标准报告FIPS46-3中推荐使用 k 1 = k 3 进行多重加密，此时密钥长度为112比特（即56比特×2）。
加密算法定义如下：
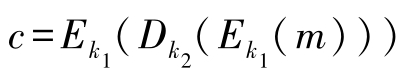
解密算法定义如下：
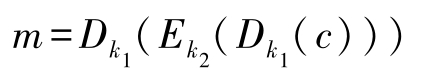
例3-6 三重DES加密示例
设明文 m =“computer”，密钥 k =“programgramproprogram”，经过3DES加密之后，得到密文 c =0x95c560a3a9591798。
（3）AES和IDEA
DES已走到了生命的尽头，56比特密钥实在太短，三重DES只是在一定程度上解决了密钥长度的问题。另外，DES的设计主要针对硬件实现，而今在许多领域都需要有软件的实现方法，在这种情况下，DES的效率相对较低。1997年4月15日，美国国家标准技术研究所（NIST）发起征集高级加密标准（Advanced Encryption Standard，AES）算法的活动，并成立了AES工作组，目的是确定一个非保密的、公开的、全球免费使用的加密算法，用于保护敏感信息。AES的基本特点是：比三重DES快，至少和三重DES一样安全，分组长度为128比特，密钥长度为128、192、256比特。
2000年10月，美国国家标准技术研究所选择Rijndael密码作为高级加密标准。Rijndael密码是一种迭代型分组密码，由比利时密码学家Joan Daemon和Vincent Rijmen设计，使用了有限域上的算术运算。该密码的数据分组长度和密钥长度都可变，并可被独立指定为128、192或256比特，分组长度不同，迭代次数也不同。可在很多处理器和专用硬件上高效地实现Rijndael密码。
国际数据加密算法（International Data Encryption Algorithm，IDEA）是由瑞士联邦理工学院的Xuejia Lai和James Massey等人于1990年提出的，能够抵抗差分密码分析。IDEA算法使用128比特的输入密钥 k ，将64比特的明文分组 m 加密成64比特的密文分组 c 。著名的电子邮件安全软件PGP（Pretty Good Privacy）就采用了IDEA算法进行数据加密。
（4）SM1、SM4和SM7
SM1算法是一种分组对称算法，分组长度和密钥长度都为128比特，算法安全性能与AES相当，算法不公开，仅以IP核的形式存在于芯片中，需要通过加密芯片的接口调用该算法时。该算法已经参与研制了系列芯片、智能IC卡、智能密码钥匙、加密卡、加密机等安全产品，广泛应用于电子政务、电子商务及国民经济的各个应用领域。
SM4为无线局域网标准的分组加密算法，用于替代DES、AES等国际算法，SM4算法与AES算法具有相同的密钥长度和分组长度，均为128比特。
SM7算法是一种分组密码算法，分组长度和密钥长度均为128比特。它跟SM1一样，是不被公开的，需要添加加密芯片才能调用。SM7适用于非接触式IC卡，应用包括身份识别类应用（门禁卡、工作证、参赛证）、票务类应用（大型赛事门票、展会门票）、支付与通卡类应用（积分消费卡、校园一卡通、企业一卡通等）。
公钥密码学的基本思想是公开密钥。为了保证公钥密码系统的安全，必须确保从公钥 k e 计算私钥 k d 是不可行的、密钥空间足够大，以及存在有效的算法实现随机选择密钥。公钥密码的安全性取决于某些困难数学问题的难解性。公钥密码中常用的难解问题有大整数分解问题、离散对数问题、椭圆曲线上的离散对数问题等。RSA、ElGamal和ECC是国际上普遍使用的公钥加密方法的典型代表，国密算法中的SM2和SM9也属于公钥加密体制。
1.RSA加密方法
1977年，美国麻省理工学院的三位数学家Ron Rivest、Adi Shamir和Len Adleman成功地设计了一个公钥密码算法，该算法根据设计者的名字被命名为RSA算法。在其后的30年中，RSA成为世界上应用最为广泛的公钥密码算法。RSA密码的安全性基于大整数分解的困难性。若已知两个大素数 p 和 q ，求 n = pq 是容易的，而反过来由 n 求 p 和 q 则是困难的，这就是大整数分解问题。
RSA算法分为密钥生成、加密和解密三个阶段。在密钥生成阶段，密钥生成算法执行以下3个步骤。
1）选择不同的大素数 p 和 q ，计算 n = p · q ， φ （ n )=（ p -1)（ q -1)。
2）选择 e ，满足 I ＜ e ＜ φ （ n ），且gcd（ e , φ （ n ））=1，（ n , e ）作为公钥。
3）通过 ed ≡1mod φ （ n ）计算 d ，满足 e ≠ d ，（ n , d ）作为私钥。
其中， n 、 e 、 d 分别为模数、加密指数和解密指数， φ ( n ）是 n 的欧拉函数值， d 是 e 在模 φ ( n ）下的乘法逆元，即 d = e -1 mod φ ( n ）。
在加密和解密阶段，加密时首先对明文比特串分组，使每个分组对应的十进制数小于 n ，即分组长度小于log 2 n 。对 Z n ={0,1,…, n -1}范围内的消息 m 进行加密。
加密函数定义如下：
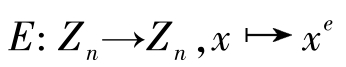
解密函数定义如下：
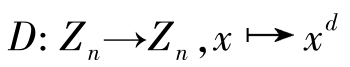
映射 E 和 D 彼此互逆，即对于任意明文 m ∈ Z n ，
加密算法定义如下：
c ≡ m e (mod n )
解密算法定义如下：
m ≡ c d (mod n )
例3-7 RSA应用示例：Alice向Bob发送加密消息
Bob：选取 p =101、 q =113，计算
n = p · q =101×113=11413
φ ( n )=( p -1)( q -1)=100×112=11200
选取 e =3533，验证
gcd( e , φ ( n ))=gcd(3533,11200)=1
计算
d ≡ e -1 mod φ ( n )=3533 -1 mod 11200=6597
Bob公钥（ n , e ）=（11413,3533），私钥（ n , d ）=（11413,6597）。
Alice：想加密明文 m =9726，计算
c ≡ m e (mod n )=9726 3533 (mod 11413)=5761
并把密文 c =5761传送给Bob。
Bob：收到密文 c =5761后，计算
m ≡ c d (mod n )=5761 6597 (mod 11413)=9726
2.ElGamal加密方法
ElGamal密码是1985年由T.ElGamal提出的，它是基于离散对数问题的最著名的公钥密码体制。若给定一个大素数
p
，
p
-1有一个大素数因子，则可构造一个乘法群
，
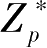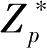是一个
p
-1阶循环群。设
g
是
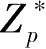的一个本原根，且1＜
g
＜
p
-1，若已知
x
求
y
=
g
x
mod
p
是容易的，而由
y
、
g
、
p
求
x
，使得
y
=
g
x
mod
p
成立则是困难的，这就是离散对数问题。
ElGamal算法分为密钥生成、加密和解密三个阶段。在密钥生成阶段，密钥生成算法执行以下3个步骤。
1）选择大素数
p
，使
p
-1有大素数因子，选择
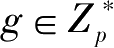为本原根。
2）随机选择整数 d ，满足1≤ d ≤ p -2， d 为私钥。
3）计算 e ≡ g d （mod p )， e 为公钥。
其中， p 、 g 和 e 公开，为所有用户所共享， d 保密。
在加密和解密阶段，对消息
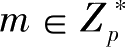进行加密，随机选择整数
k
，满足1≤
k
≤
p
-2。加密函数定义如下：
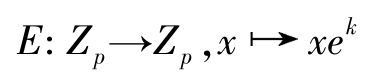
解密函数定义如下：
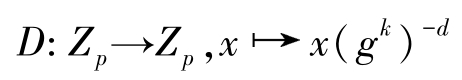
即对于任意明文
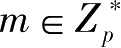，随机整数1≤
k
≤
p
-2，加密算法定义如下：
c 1 ≡ g k (mod p )
c 2 ≡ me k (mod p )≡ mg dk (mod p )
解密算法定义如下：
m ≡ c 2 ( c 1 ) -d (mod p )≡ mg dk ( g k ) -d (mod p )
加密结果依赖于消息 m 、公钥 e 和随机整数 k 。如果随机整数 k 的选择与消息 m 无关，那么几乎不可能出现两个明文生成同一个密文的情况。
例3-8 ElGamal应用示例：Alice向Bob发送加密消息
Bob：选取素数
p
=2357，
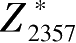上的本原根
g
=2，私钥
d
=1751，计算
e ≡ g d (mod p )=2 1751 (mod 2357)=1185
e =1185为Bob公钥。
Alice：想加密明文 m =2035，随机选取整数 k =1520，计算
c 1 ≡ g k (mod p )≡2 1520 (mod 2357)=1430
c 2 ≡ me k (mod p )≡2035×1185 1520 (mod 2357)=697
将密文（ c 1 , c 2 ）=（1430,697）传送给Bob。
Bob：收到密文（ c 1 , c 2 )=（1430,697）后，计算
算法中离散对数的复杂性决定了系统的安全，然而，算法的设计是基于
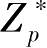群是
p
为模的同余乘法群，对乘法满足封闭性，且存在乘法逆元。如果
p
不是素数，则（模
p
）同余类群
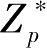只能是以加法为运算的整数群，只存在加法逆元且只对加法满足封闭性，离散对数的关系就不存在了。
3.ECC加密方法
椭圆曲线理论是代数几何、数论等多个数学分支的定义，曾被认为是一个纯理论学科，20世纪80年代被引入密码学后，由于它的复杂性高、密钥短、占用资源少等优点，引起了人们的极大兴趣。在移动通信中的应用进一步推动了对该领域研究的进展。
1985年，Koblitz和Miller分别提出利用椭圆曲线来开发公钥密码体制。椭圆曲线密码（Elliptic Curve Cryptography，ECC）的安全性基于椭圆曲线离散对数求解的困难性。目前普遍认为，椭圆曲线离散对数问题要比大整数因子分解和有限域上的离散对数问题难解得多。
椭圆曲线是满足一类方程的点的集合，通过在点间定义一种特殊的运算，可以得到一个群，称为椭圆曲线群。设 E 是某有限域上的椭圆曲线， G 是椭圆曲线 E 的一个素数阶循环子群， α 是该循环子群 G 的一个生成元， β ∈ G 是该循环子群 G 的一个元素。已知 α 和 β ，求满足 β = nα 的唯一整数 n ，称为椭圆曲线上的离散对数问题。
与RSA密码相比，ECC密码能用较短的密钥实现较高的安全性。也就是说，要达到同样的安全强度，ECC算法所需的密钥长度远比RSA算法短，并且随着加密强度的提高，ECC的密钥长度变化不大（如表3-4所示）。
表3-4 RSA和ECC的性能比较
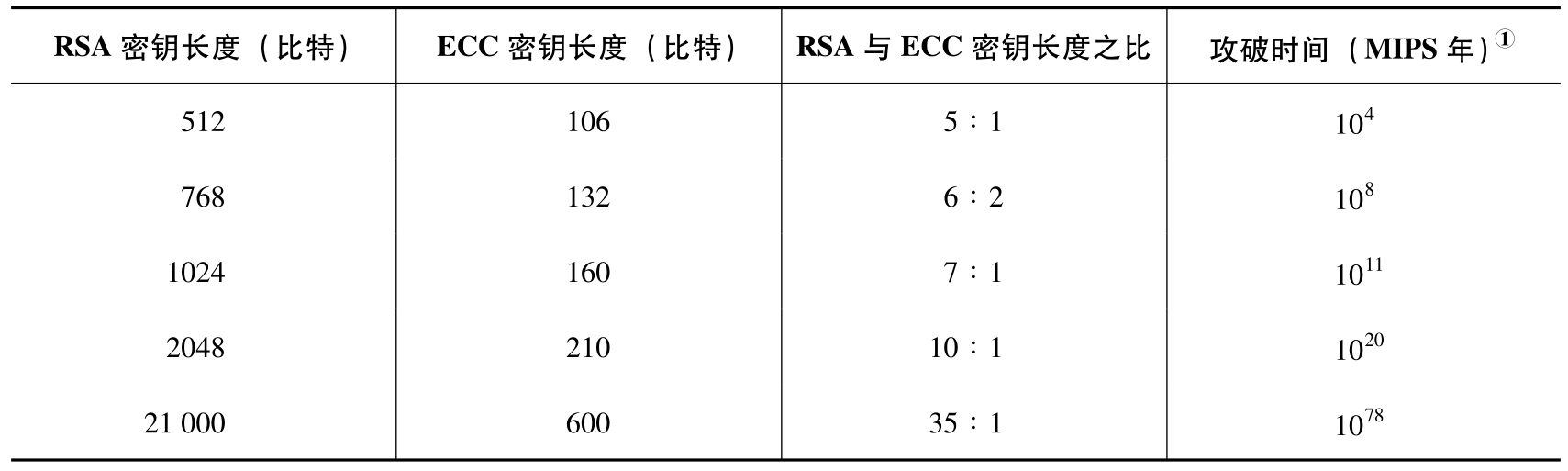
①MIPS年是指以MIPS（Millions of Instructions Per Second，CPU的速度达到每秒执行百万条指令）级的计算机来运算所需的攻破时间。
为了用好ECC加密方法，需要先来认识椭圆曲线。设 p 是一个大于3的素数， F p 是模 p 的有限域， F p 上的椭圆曲线 E 定义为
E ： y 2 ≡ x 3 + ax + b (mod p )
其中， a , b , x , y ∈ F p 且满足
4 a 2 +27 b 3 ≠0(mod p )
E （ F p ）表示椭圆曲线 E 上的所有点（ x , y ）和无穷远点 O 的集合，也记为 E p （ a , b ），或者直接记为 E 。
在椭圆曲线 E 上按如下法则定义加法运算：
· 定义无穷远点 O 为加法单位元，对于任意点 P ∈ E ，有
P +0=0+ P
· 若 P =( x , y )∈ E ，定义 -P =( x , -y )，( x , y )+( x , -y )= O 。
· 若 P =( x 1 , y 1 )∈ E ， Q =( x 2 , y 2 )∈ E ，定义 P + Q =( x 3 , y 3 )，其中，
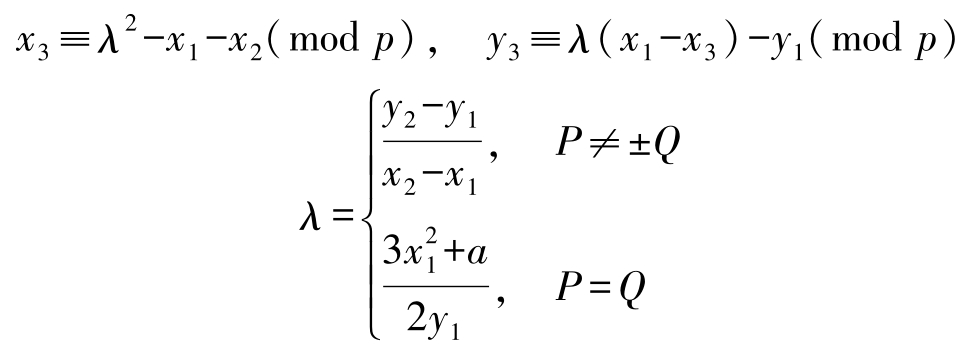
例3-9 椭圆曲线点乘示例
设 a =1、 b =6、 p =11，椭圆曲线方程为
E ： y 2 ≡ x 3 + x +6(mod 11)
计算 E 11 （1,6）={ O ,（2,4）,（2,7）,（3,5）,（3,6）,（5,2）,（5,9）,（7,2）,（7,9）,（8,3）,（8,8）,（10,2）,（10,9）}。
为了求得椭圆曲线 E 上的点 E 11 （1,6），取 P =（2,7），计算
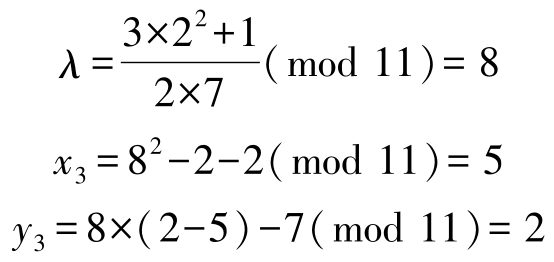
进一步计算点乘
P =(2,7)，2 P =(5,2)，3 P =(8,3)，4 P =(10,2)，5 P =(3,6)，6 P =(7,9)，
7 P =(7,2)，8 P =(3,5)，9 P =(10,9)，10 P =(8,8)，11 P =(5,9)，12 P =(2,4)，
13 P = O
结果表明：椭圆曲线 E 有13个点， E 11 （1,6）是一个循环群， P =（2,7）是椭圆曲线 E 的生成元。研究表明，任意素数阶的群是循环群，任何非无穷远点都是 E 的生成元。
椭圆曲线上的公钥加密方法有两种方案：方案1，将明文 m 编码为椭圆曲线上的点 P m =( x m , y m )；方案2，将明文 m 限定为 m ∈ F p 。每种方案都包括密钥生成、加密和解密三个阶段，下面分别介绍这两种方案。
方案1
在密钥生成阶段，Alice和Bob在椭圆曲线 E p ( a , b ）上选取大的素数阶 n 和生成元 P ，Alice和Bob共享椭圆曲线的公共参数。Bob随机选取整数 a ，满足1≤ a ≤ n -1，计算 Q = a ·P则 Q 为Bob的公钥， a 为Bob的私钥。
在加密阶段，Alice将明文 m 编码为椭圆曲线 E p （ a , b ）上的点 P m =（ x m , y m ），然后随机选取整数 k ，满足1≤ k ≤ n -1，计算
c 1 = k · P =( x 1 , y 1 )
c 2 = P m + k · Q =( x 2 , y 2 )
得到密文为（ c 1 , c 2 ），并将密文（ c 1 , c 2 ）传送给Bob。
在解密阶段，Bob收到密文（ c 1 , c 2 ）后，计算
P m = c 2 -a · c 1
再对 P m 解码得到明文 m 。
方案2
在密钥生成阶段，密钥生成算法与方案1相同。在加密阶段，Alice随机选取整数 k ，满足1≤ k ≤ n -1，计算
( x 2 , y 2 )= k · Q
直到 x 2 ≠0，计算
c 1 = k · P =( x 1 , y 2 )
c 2 ≡ x 2 (mod p )
得到密文为（ c 1 , c 2 ），并将密文（ c 1 , c 2 ）传送给Bob。
在解密阶段，Bob收到密文（ c 1 , c 2 ）后，计算
（ x 2 , y 2 ）= a · c 1
然后计算
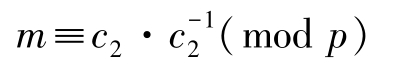
得到明文 m 。
例3-10 设有限域 F 11 上的椭圆曲线
E ： y 2 = x 3 + x +6
所有的点关于加法构成循环群， P =(2,7）是生成元。
密钥生成：Bob随机选取私钥 a =2，计算公钥 Q = a · P =2（2,7）=（5,2）。
加密：Alice要将明文 m =9（ m ∈ F 11 ）加密传送给Bob，Alice随机选取 k =3，并计算
c 1 = k · P =3（2,7）=（8,3）， k · Q =3（5,2）=（7,9），
c 2 ≡ m · x 2 （mod p ）≡9×7（mod 11）=8
得到密文（ c 1 , c 2 ）=（8,3,8），并将密文（ c 1 , c 2 ）=（8,3,8）传送给Bob。
解密：Bob收到密文（ c 1 , c 2 ）=（8,3,8）后，计算
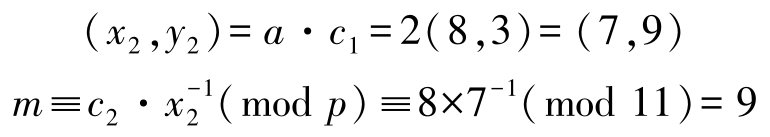
4.SM2和SM9
SM2算法是我国在吸收国际先进成果的基础上研制的具有自主知识产权的椭圆曲线公钥密码算法（ECC），在我国商用密码体系中被用来替换RSA算法。相较于RSA算法，SM2算法是一种更先进、更安全的算法，256比特的SM2密码强度已经比2048比特的RSA密码强度要高。SM2算法就是ECC椭圆曲线密码机制，但在签名、密钥交换方面不同于ECDSA、ECDH等国际标准，而是采取了更为安全的机制。另外，SM2还推荐了一条256比特的曲线作为标准曲线。
SM9算法是在有限域中利用椭圆曲线上双线性对构造的基于标识的密码算法。不同于传统的公钥密码算法，SM9算法不需要通过传统公钥基础设施（PKI）体系中的证书认证中心（CA）等保证用户公钥来源的真实性，SM9算法将用户的唯一标识信息（如手机号码、邮箱地址等）作为公钥，省略了交换数字证书和公钥的过程，极大地减少了计算和存储资源的开销。SM9算法适用于互联网各种新兴应用的安全保障，如基于云技术的密码服务、电子邮件安全、智能终端保护、物联网安全、云存储安全等。这些安全应用可采用手机号码或邮件地址作为公钥，实现数据加密、身份认证、通话加密、通道加密等。在商用密码体系中，SM9主要用于用户的身份认证，SM9的加密强度等同于3072比特密钥的RSA加密算法。