




样本选择主要基于以下原则:首先,必须是流动性好、用途广,且在实践中备受银行欢迎的质物;其次,有足够的样本数据,且来源可靠,最后尽量选择相关性较弱的质物,以满足银行构建组合分散风险的初衷。考虑到以上几点,以重要的工业原材料——长江现货1#铜、长江现货A00铝和西本螺纹钢(HRB400,j16)三种质物(以下,分别简称铜、铝和螺纹钢)的每日交易均价为样本,三者均为相应期货交割的标准品,具有很强的代表性
 ,样本区间为2005年1月4日—2011年10月31日,为了避免节假日造成数据伪相关,在此只对三个样本均存在交易的情况做统计,并未做任何插值处理,样本区间内共计1 657个样本点,并将前1 412个观测值作为样本内数据估计模型参数,剩余的245个观察值作为样本外数据评价模型效果。
,样本区间为2005年1月4日—2011年10月31日,为了避免节假日造成数据伪相关,在此只对三个样本均存在交易的情况做统计,并未做任何插值处理,样本区间内共计1 657个样本点,并将前1 412个观测值作为样本内数据估计模型参数,剩余的245个观察值作为样本外数据评价模型效果。
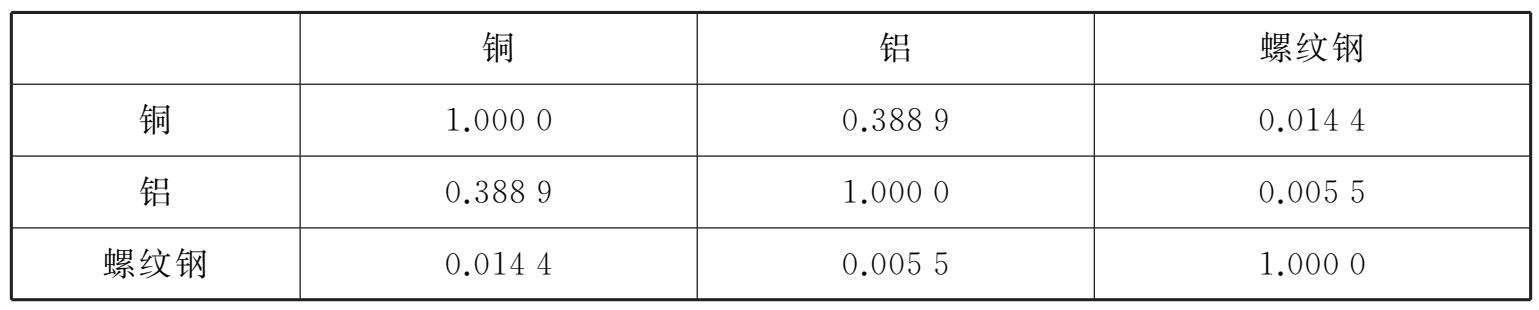
三个样本的对数收益率时间序列和Kendall秩相关系数矩阵分别如图2-1和表2-1所示。观察表2-1不难发现,铜和螺纹钢具有较弱的相关性,而铜和铝相关性则相对较强,因此,本章通过构造弱相关组合(铜和螺纹钢)和强相关组合(铜和铝)两组质物组合分别建立Copula-GARCH模型以进一步验证模型的有效性。
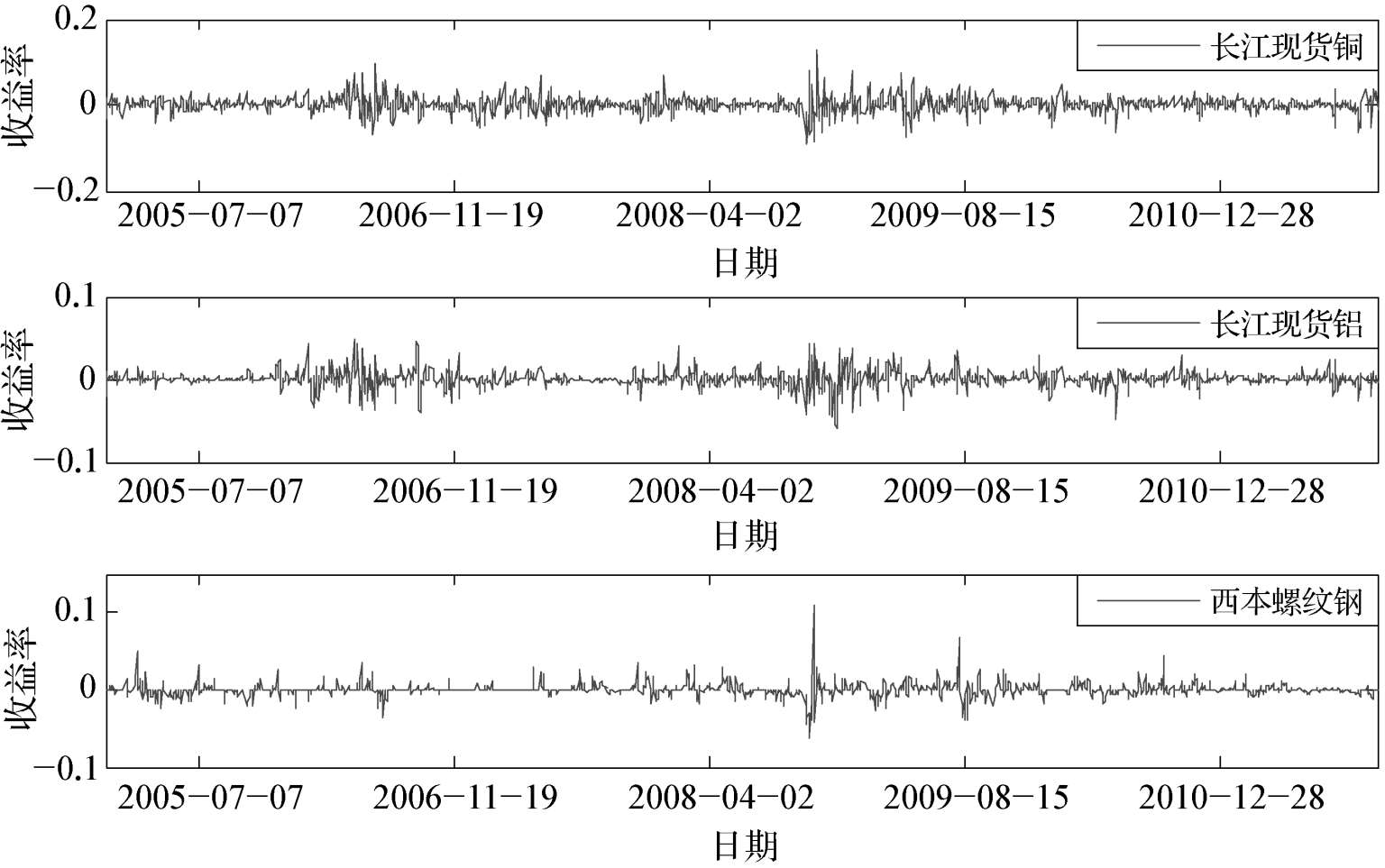
图2-1 铜、铝以及螺纹钢的对数收益率序列图
表2-1 铜、铝和螺纹钢三种质物对数收益率的Kendall秩相关系数τ矩阵
从图2-1可以直观地看到,铜、铝以及螺纹钢的对数收益率表现出较为显著的波动集聚特征,而且在2008年金融危机前后,这一现象更为显著,这也印证了三者在金融危机中均遭遇大幅跳水。接下来对上述三者样本内的收益率进行详细的统计性描述,如表2-2所示,可以发现三者的收益率均存在“尖峰厚尾”这一典型事实(峰度显著大于3,J-B正态性检验未通过),而且经过ADF单位根检验,在1%的水平下拒绝原假设,说明三个样本的对数收益率序列是平稳的,可以对序列进行建模分析。
表2-2 铜、铝以及螺纹钢的对数收益率描述性统计及ARCH效应检验
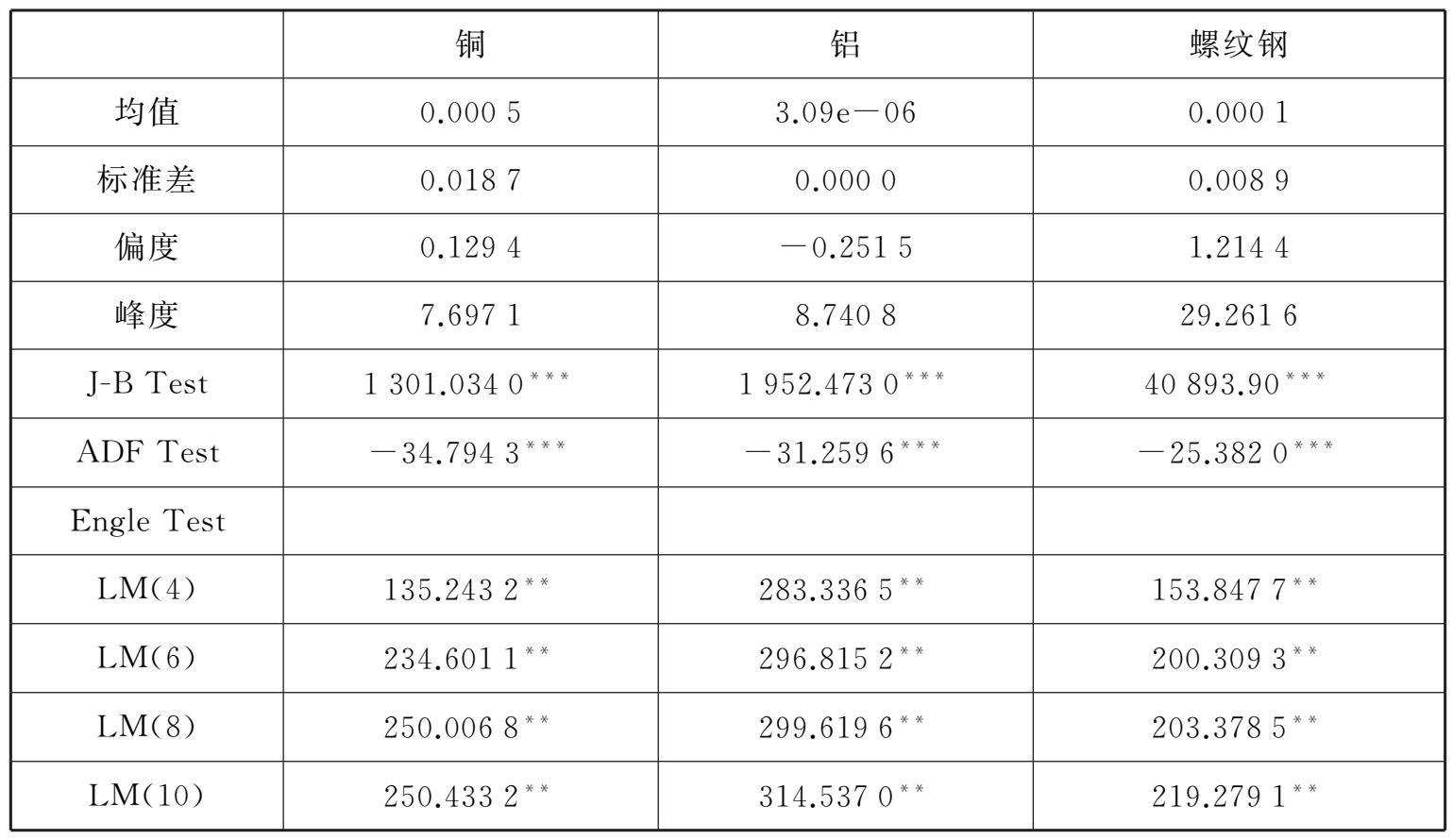
注:**表示在5%的水平下显著,***表示在1%的水平下显著,J-B Test为正态性检验,ADF单位根检验为平稳性检验,Engle Test为ARCH效应检验。
最后对样本的对数收益率进行自相关检验和ARCH效应检验。其中,运用Engle LM检验法对ARCH效应检验时,当滞后阶数为10阶时,LM(10)仍在5%的水平下拒绝原假设,表明存在显著的ARCH效应,结果如表2-2所示。而通过图2-2可以发现,样本自相关函数和部分自相关函数确实呈现了相关性,尤其是螺纹钢和铝的收益率呈现出显著的一阶自相关性,铜的收益率在1阶、3阶、4阶均有较弱的相关性。因此,接下来运用ARMA-GARCH族模型对铜和螺纹钢进行条件均值和条件方差建模。
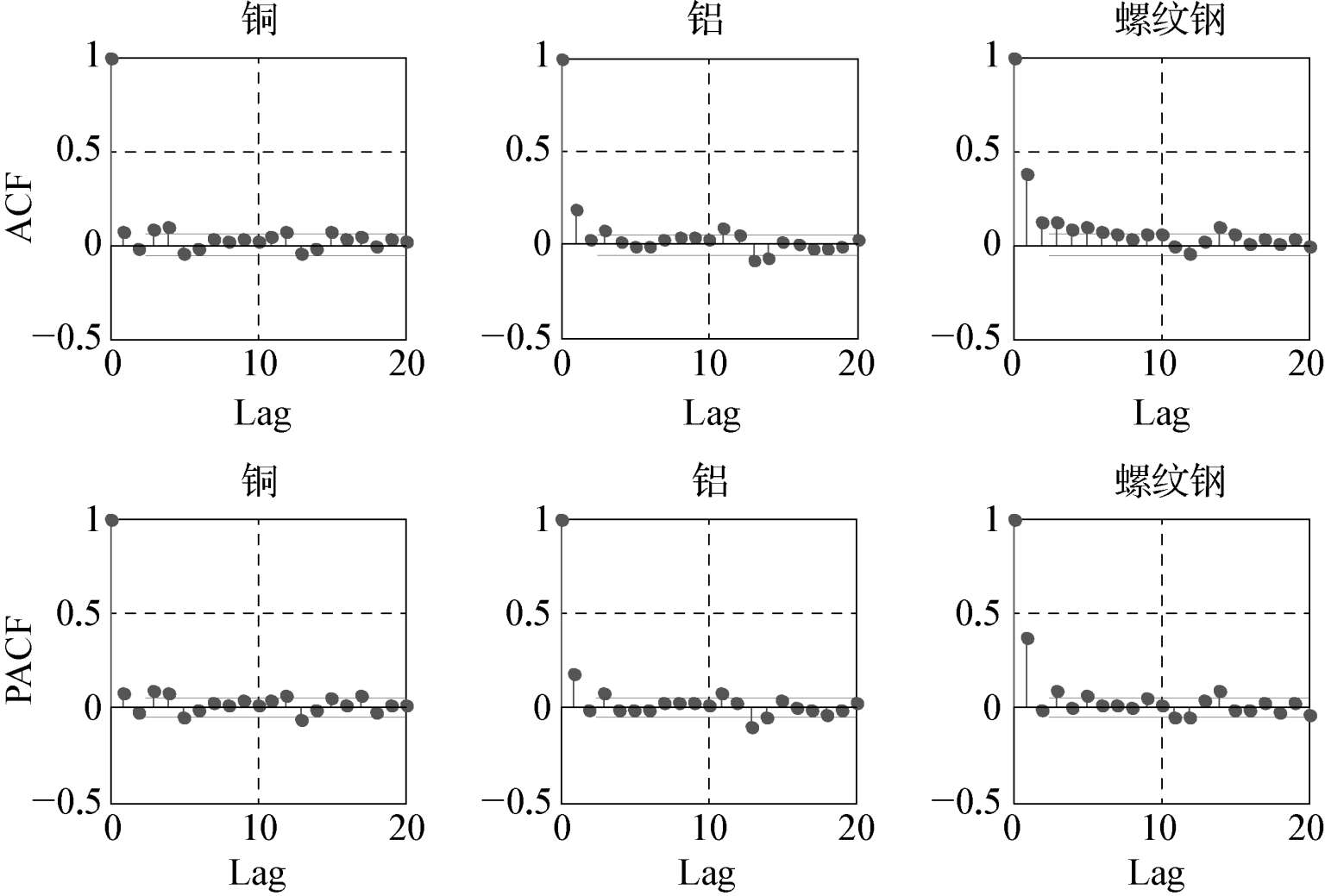
图2-2 铜、铝以及螺纹钢收益率的自相关和偏自相关图
综合考虑以上因素,采用ARMA-GARCH模型族对铜和螺纹钢的对数收益率进行建模,模型选择依据是在各参数显著的条件下,依据AIC准则和似然值的大小选取。因此,虽然铜的对数收益率在3阶和4阶依然存在自相关(见图2-2),但运用GARCH模型估计时,其参数并不显著,故条件均值方程应用的是参数显著的ARMA(1,1)模型。其参数估计结果如表2-3所示。
表2-3 三类现货资产条件均值和条件方差方程的参数估计结果
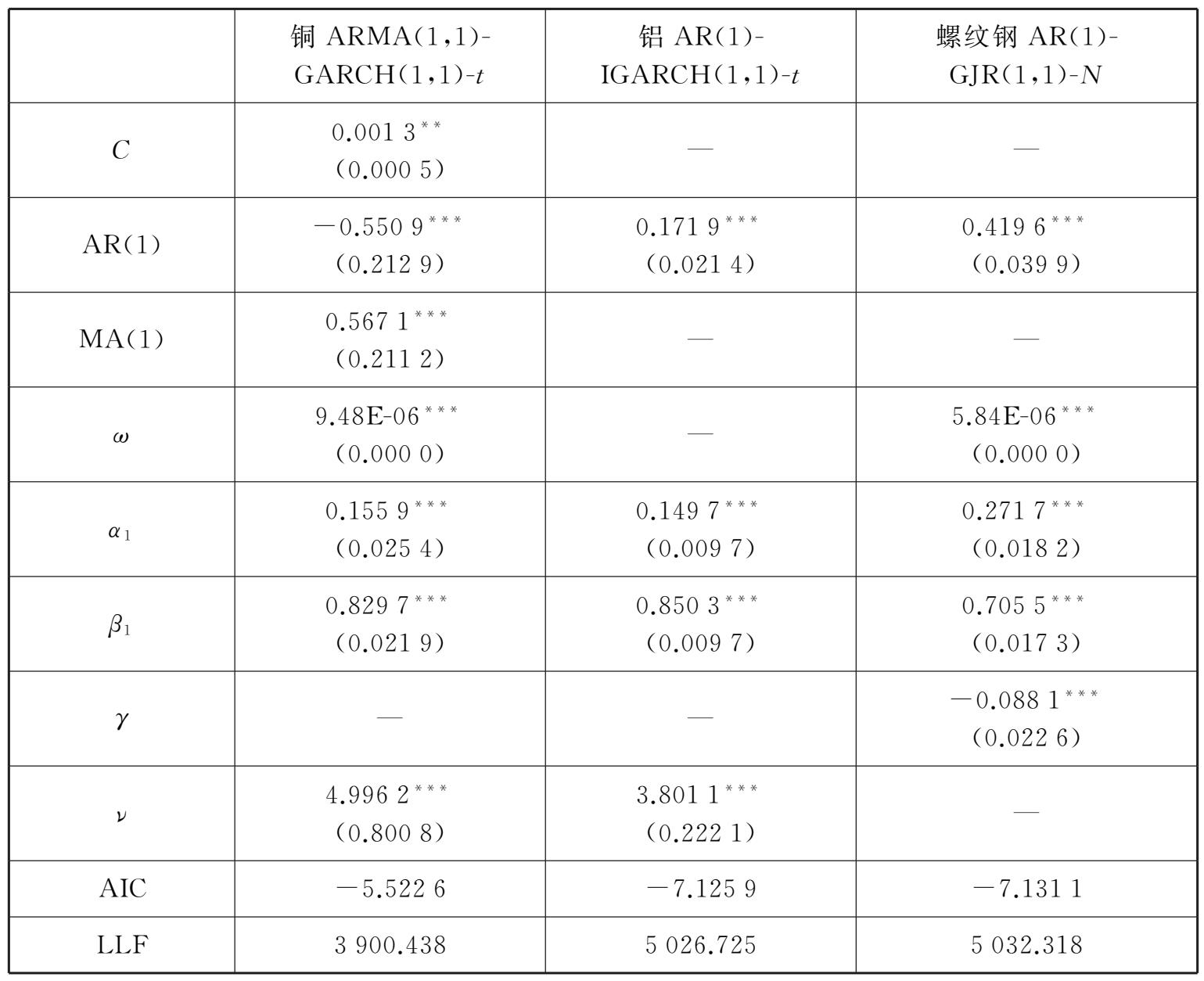
注:**表示在5%的水平下显著,***表示在1%的水平下显著,表中数字为各参数估计结果,圆括号内为标准误差。
通过表2-3可以看到
t
分布下的ARMA(1,1)-GARCH(1,1)模型可以较好地刻画铜的对数收益率的波动集聚性及时变性,其中,
 ,且
,且
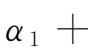
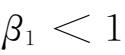 ,满足模型参数的非负条件及平稳性条件,其他各项参数均较为显著。对于铝,一般的GARCH族模型不能满足平稳性条件,因此运用特殊的AR(1)-IGARCH(1,1)-
t
模型进行拟合。而对于螺纹钢,正态分布下AR(1)-GJR(1,1)模型刻画其波动率最为合适,其中,
,满足模型参数的非负条件及平稳性条件,其他各项参数均较为显著。对于铝,一般的GARCH族模型不能满足平稳性条件,因此运用特殊的AR(1)-IGARCH(1,1)-
t
模型进行拟合。而对于螺纹钢,正态分布下AR(1)-GJR(1,1)模型刻画其波动率最为合适,其中,
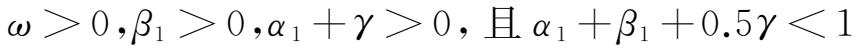 ,满足模型参数非负及平稳性条件,但非对称杠杆项系数为负值。这表明螺纹钢现货市场不同于传统金融市场表现出较强的杠杆效应,而是与之相反,利空消息对市场的冲击要小于利好消息对市场带来的冲击,但这一现象并不显著。究其原因,一方面由于现货市场的流动性要小于证券期货市场;另一方面,现货市场的参与者更多的是较为理性的且具有真实贸易背景的企业,投机或者非理性的散户投资者较少。
,满足模型参数非负及平稳性条件,但非对称杠杆项系数为负值。这表明螺纹钢现货市场不同于传统金融市场表现出较强的杠杆效应,而是与之相反,利空消息对市场的冲击要小于利好消息对市场带来的冲击,但这一现象并不显著。究其原因,一方面由于现货市场的流动性要小于证券期货市场;另一方面,现货市场的参与者更多的是较为理性的且具有真实贸易背景的企业,投机或者非理性的散户投资者较少。
首先将基于ARMA-GARCH族模型刻画边缘分布得到的标准残差项,经过概率积分变换为(0,1)均匀分布,绘制散点图,如图2-3所示。
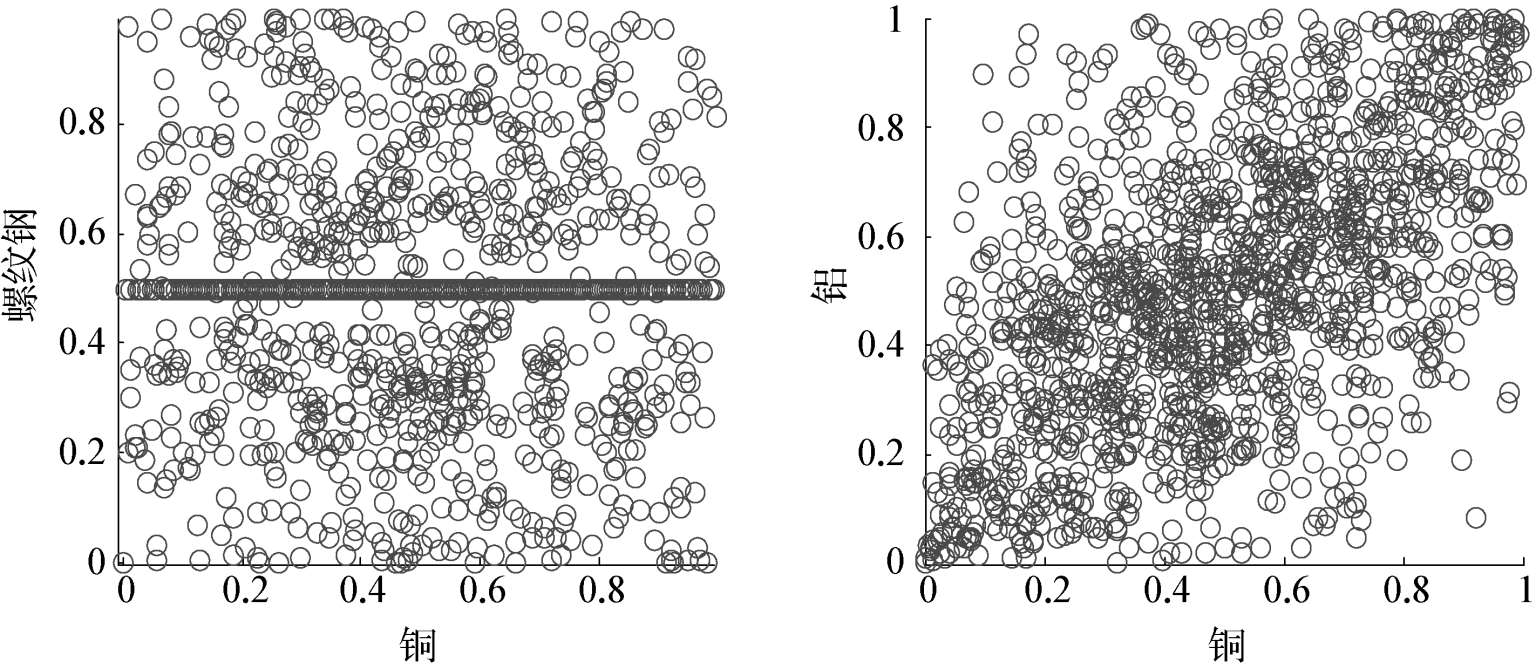
图2-3 铜和螺纹钢以及铜和铝的收益率的标准残差项经概率积分变换后的散点图
图2-3中,铜和螺纹钢的收益率的标准残差项经概率积分变换后的散点图呈无规律分布状态,并无显著的线性相关现象,但在纵轴为0.5时,散点图较为密集,这主要是由螺纹钢的交易不活跃,连续几个交易日价格无变化,致使对数收益率为0引起的,这也正体现了现货资产与股票、期货等交易活跃的金融资产的区别。与此相比,铜和铝的收益率的标准残差项经概率积分变换后的散点图则表现出显著的正相关。接下来,对n-Copula,t-Copula,Clayton-Copula,Gumbel-Copula以及Frank-Copula函数进行参数估计,并运用平方欧氏距离进行拟合度检验,结果如表2-4和表2-5所示。
表2-4 铜和螺纹钢组合五种Copula函数的Kendall秩相关系数及与经验Copula函数的拟合度
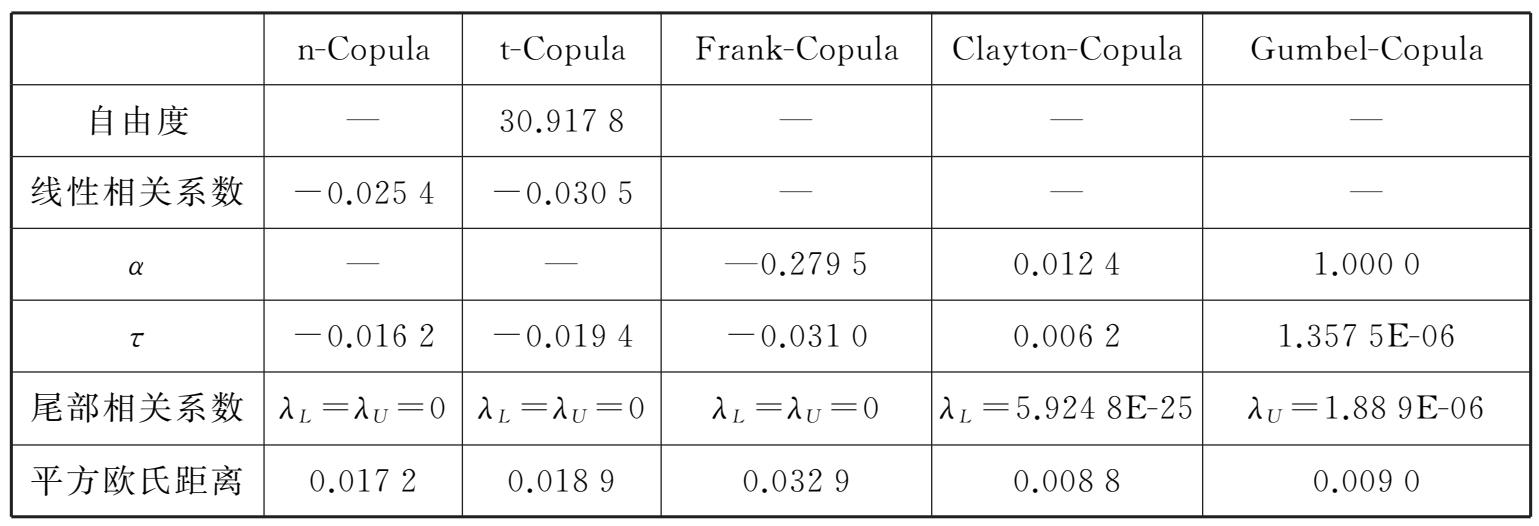
表2-5 铜和铝组合五种Copula函数的Kendall秩相关系数及与经验Copula函数的拟合度
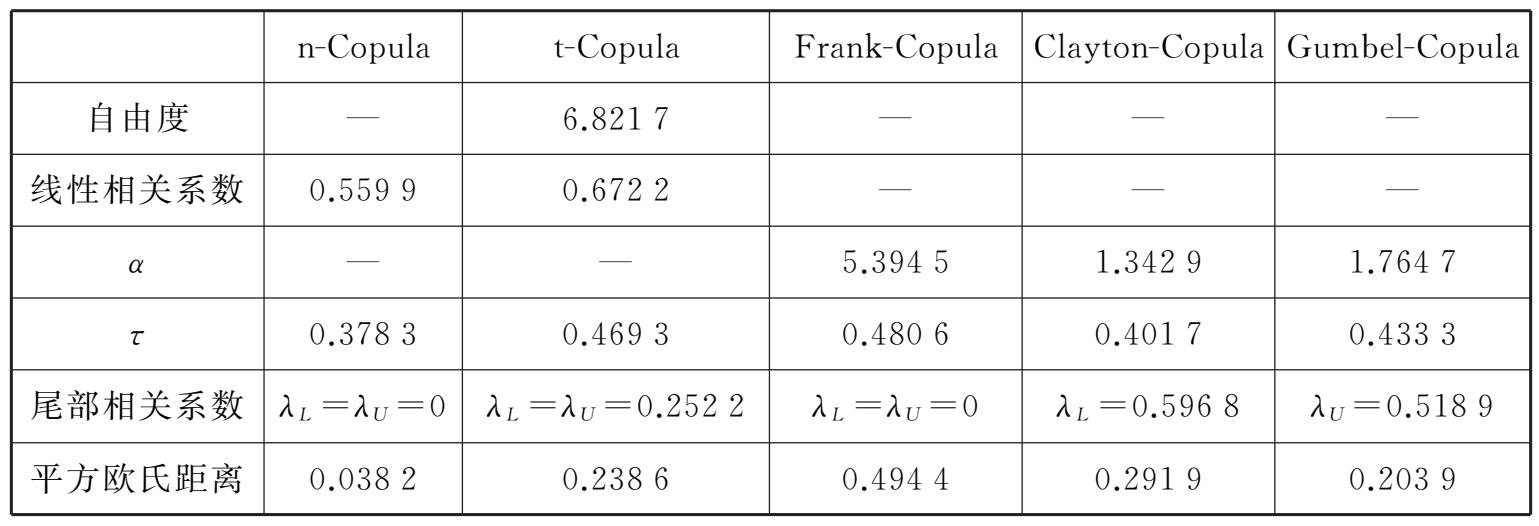
表2-4中,无论是线性相关系数、Kendall秩相关系数τ还是尾部相关系数均表明铜与螺纹钢确实呈现较弱的相关性,而从平方欧氏距离对估计Copula函数的检验来看,虽然Clayton-Copula函数表现最优,但总体而言,五类Copula函数并无显著区别,这虽与现有学者大量关于运用Copula刻画相关性极强的变量间的关系得到的结论不一致,但针对弱相关的质物组合而言,却也符合现实逻辑。与此相比,表2-5中线性相关系数、Kendall秩相关系数以及尾部相关系数则表明铜和铝确实表现出较强的相关性,且n-Copula函数的平方欧氏距离最小,拟合度最优。但进一步研究表明,拟合度最优的Copula函数预测的VaR值不一定最为精确,而且到目前为止,识别最优拟合Copula的问题并未得到有效解决。因此,为了得到更为精确的风险预测结果,分别运用上述五类Copula函数通过蒙特卡洛模拟产生5组10 000×2随机数矩阵(
u
,
v
),进一步依据模型设定部分阐述的模拟计算过程,得到五类Copula函数产生的5组10 000×2质物组合的收益率向量
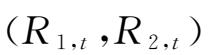 ,从而进一步展开质物组合的VaR模拟及其失效率检验。
,从而进一步展开质物组合的VaR模拟及其失效率检验。
为计算方便,我们假设两组质物组合中质物具有相同的权重,即
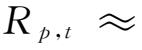
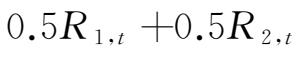 。此外,鉴于样本外预测的结果较之于样本内的结果更加可靠且更具实用性,而且为了避免多期预测带来的不精确问题,此处采取滚动时间窗的样本外预测方法,即首先利用样本内数据(
t
=1,2,…,1 412),预测样本外第一天(
t
=1 413)的VaR,接着,保持估计样本数量不变(
n
=1 412),将样本向后平行移动1个交易日,即运用
t
=2,3…,1 413的观测值估计
t
=1 414交易日的VaR,以此类推,至最后交易日。除此之外,还引入历史模拟法(Hs)和Risk Metrics经常使用的EWMA模型对质物组合的收益率
R
p
进行VaR预测,其中,EWMA模型中滚动窗口的设定与Copula模型保持一致(
n
=1 412),而考虑到历史模拟法的精确度受样本影响更大,实证研究以及银行实践中在权衡精确性和稳定性后,通常取值250~750天(Jorion,2007),在此取500天。五类二元Copula函数以及历史模拟法和EWMA风险预测结果以及回测结果分别如图2-4和表2-6所示。
。此外,鉴于样本外预测的结果较之于样本内的结果更加可靠且更具实用性,而且为了避免多期预测带来的不精确问题,此处采取滚动时间窗的样本外预测方法,即首先利用样本内数据(
t
=1,2,…,1 412),预测样本外第一天(
t
=1 413)的VaR,接着,保持估计样本数量不变(
n
=1 412),将样本向后平行移动1个交易日,即运用
t
=2,3…,1 413的观测值估计
t
=1 414交易日的VaR,以此类推,至最后交易日。除此之外,还引入历史模拟法(Hs)和Risk Metrics经常使用的EWMA模型对质物组合的收益率
R
p
进行VaR预测,其中,EWMA模型中滚动窗口的设定与Copula模型保持一致(
n
=1 412),而考虑到历史模拟法的精确度受样本影响更大,实证研究以及银行实践中在权衡精确性和稳定性后,通常取值250~750天(Jorion,2007),在此取500天。五类二元Copula函数以及历史模拟法和EWMA风险预测结果以及回测结果分别如图2-4和表2-6所示。
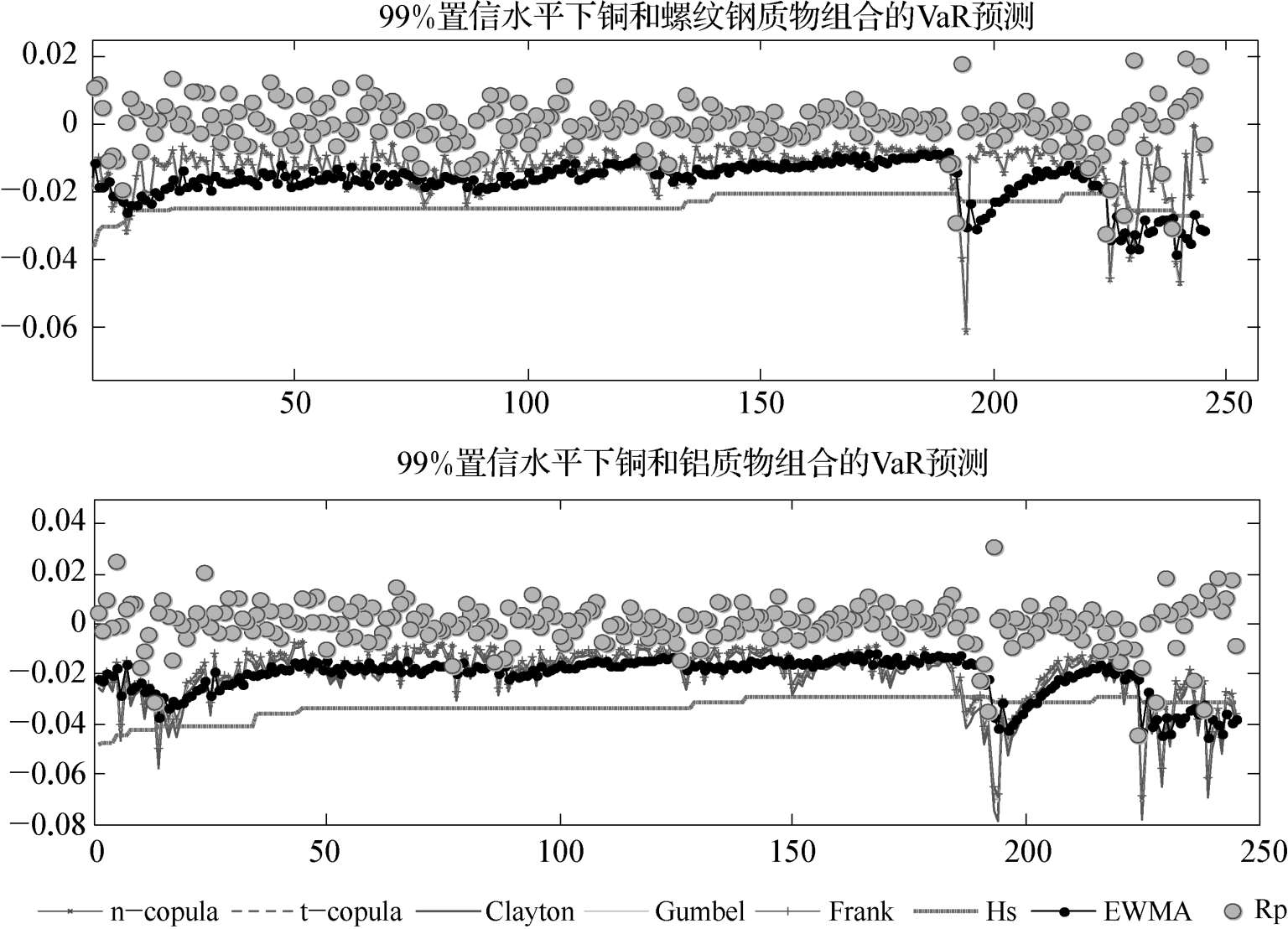
图2-4 99%置信水平下五种Copula函数与历史模拟法、EWMA预测VaR对比
表2-6 不同模型下99%置信水平两组质物组合VaR回测检验
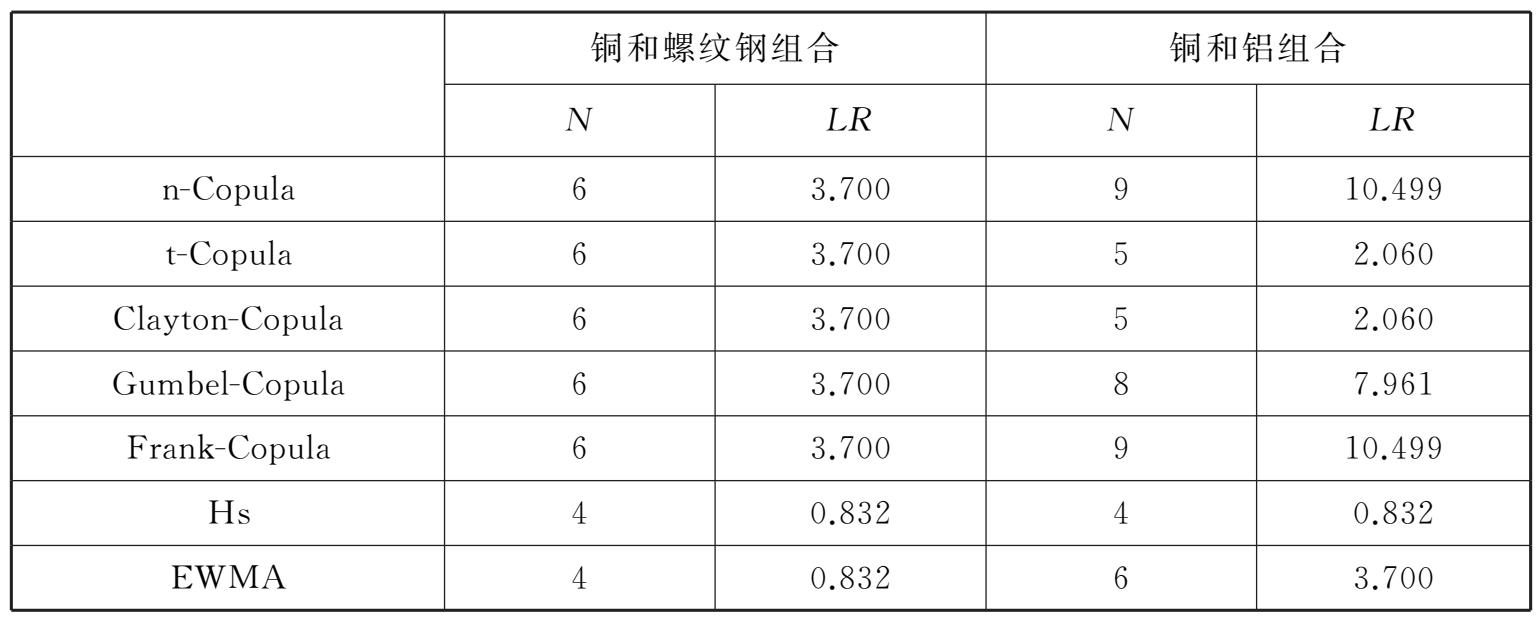
图2-4和表2-6清晰地证实,99%的置信水平下,五类Copula函数在预测铜和螺纹钢这一弱相关质物组合的VaR上并无显著区别,预测值几乎重合,回测检验中例外次数均为6次,检验统计量 LR 小于3.841,说明模型有效;而在估计铜和铝这一相关性较强的组合风险时,能够捕捉上下对称尾部相关结构变化的t-Copula和能够捕捉下尾变化的Clayton-Copula,例外次数均为5次, LR 值小于3.841,合理地估计了风险,但无法捕捉尾部结构变化的n-Copula,Frank-Copula以及仅能捕捉上尾部结构变化的Gumbel-Copula无法通过检验,低估了风险。与此相比,实践中广泛使用的历史模拟法和EWMA虽不能详尽刻画质物资产收益率间相关结构的变化,但均能估计风险。上述结果表明,对于持有质物多头头寸的商业银行而言,五类Copula函数中能够捕捉尾部损失的t-Copula和Clayton-Copula具有更高的精度。但与此同时也客观地说明Copula-GARCH族模型在详尽展现质物间相关结构的同时,风险预测的整个过程中也面临一定程度的模型风险,一方面以现货方式交易的质物,其收益率在GARCH族模型拟合过程中往往需要近似估计,这容易造成误差,而随之Copula函数的拟合及对标准残差项的蒙特卡洛模拟将进一步放大上述误差,致使模型精度并未达到非常理想的水平。Weiβ的研究亦表明上述问题的存在。
99%置信水平下的短期动态VaR回测结果表明, t -Copula和Clayton-Copula以及历史模拟法(Hs)和EWMA方法均能估计风险。进一步,为检验质物组合分散风险的能力,分别运用上述模型对两组质物组合质押率同无风险分散化的质押率进行对比。供应链金融实践中,质押期限往往不超过1年,据此假设质押期为1年,根据模型设定部分动态质押率的设定原则,风险窗口分别假设为1周、2周、1个月、2个月、3个月、4个月、5个月、6个月、7个月、8个月、9个月、10个月、11个月以及12个月共计14个风险窗口,在此基础上,运用时间平方根法则即式(2-13)实现短期风险预测向长期风险预测的转换,从而同时克服了供应链金融实践中产品期限与风险持有期限选择以及短期数据频率与长期风险预测匹配的两大难题。最后,根据式(2-12)给出各风险窗口下考虑贷款资金成本的质押率,结果如图2-5所示。
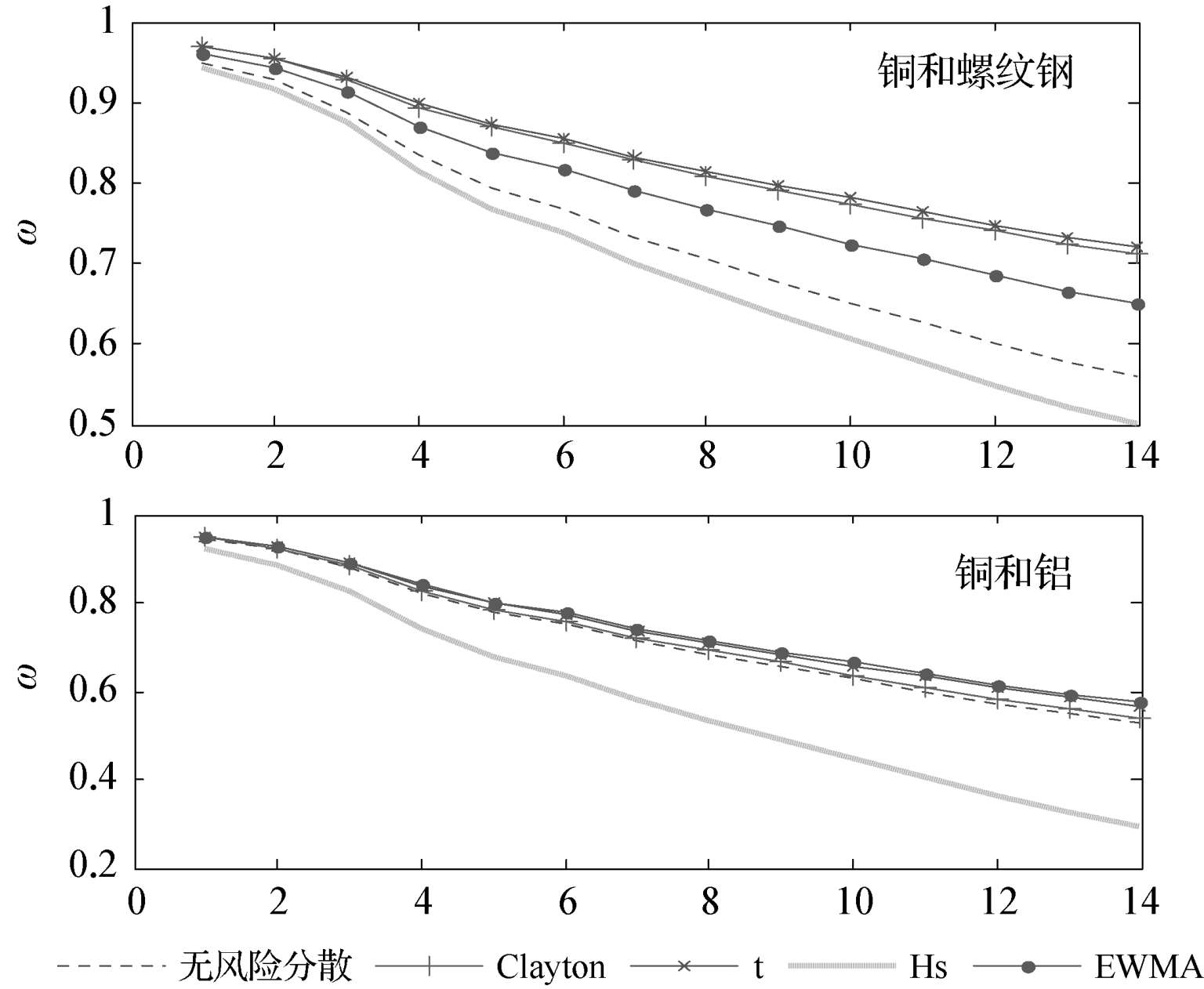
图2-5 铜和螺纹钢以及铜和铝两组质物组合分散风险效果
通过图2-5可以发现,无论是由铜和螺纹钢组成的弱相关组合抑或铜和铝组成的强相关组合,随着风险窗口的变长,质押率均呈下降趋势。进一步,与无风险分散下的VaR得到的质押率相比,弱相关质物组合分散风险的能力要强于强相关质物组合,这进一步印证了Markowitz的资产组合理论风险分散的内涵,并同时将组合内资产间的相关性越小,风险分散效果越强的结论由线性相关向非线性、尾部相关进行了完善和拓展。具体而言,在弱相关质物组合中,t-Copula以及Clayton-Copula模型风险分散效果最好,融资效率最高(其中12个月风险窗口内,相较于无风险分散得到的质押率,融资效率约可以提高27%),EWMA次之,历史模拟法最为保守,风险分散能力弱;强相关质物组合中,模型整体分散风险的能力变弱,t-Copula以及EWMA分散风险的效果最好,Clayton-Copula有所下降,而历史模拟法依然无法起到合理地分散风险效果。因此,总体而言,基于Copula-GARCH族模型在刻画组合内资产间的非线性以及尾部相关结构的同时,可以切实改善组合风险分散的效果,尤其是在弱相关性的质物组合中,这为业务实践中选取相关性较弱的质押物构成质物组合提供了决策依据。