




幂函数、指数函数、对数函数、三角函数和反三角函数,统称为基本初等函数.除反三角函数外,其他函数在以前都已学过.本节先扼要复习三角函数,再介绍反三角函数的基本概念与性质,并将基本初等函数的定义域、值域、图像和主要特性归结于一列表,方便后续学习.
常用的三角函数有正弦、余弦、正切、余切函数.正弦函数 y =sin x 与余弦函数 y =cos x 的定义域均为(-∞,+∞),周期都是2π.因为sin(- x )=-sin x ,cos(- x )=cos x ,所以正弦函数 y =sin x 是奇函数,余弦函数 y =cos x 是偶函数.又因为|sin x |≤1,|cos x |≤1,所以它们都是有界函数.图像如图1-3-1和1-3-2所示.
正切函数
y
=tan
x
的定义域为{
x
|
x
∈
R
,
x
≠
k
π+
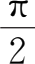 ,
k
∈
Z
},余切函数
y
=cot
x
的定义域为{
x
|
x
∈
R
,
x
≠
k
π,
k
∈
Z
}.它们的周期都是π,都是奇函数.图像如图1-3-3和1-3-4所示.
,
k
∈
Z
},余切函数
y
=cot
x
的定义域为{
x
|
x
∈
R
,
x
≠
k
π,
k
∈
Z
}.它们的周期都是π,都是奇函数.图像如图1-3-3和1-3-4所示.
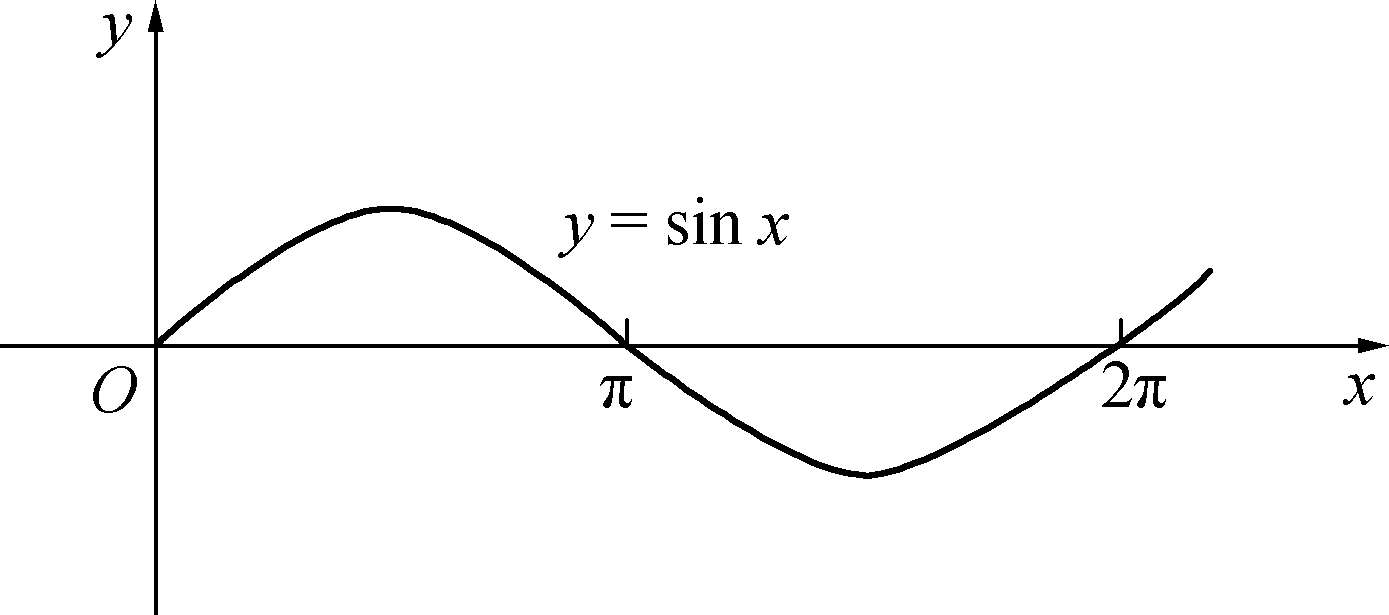
图1-3-1
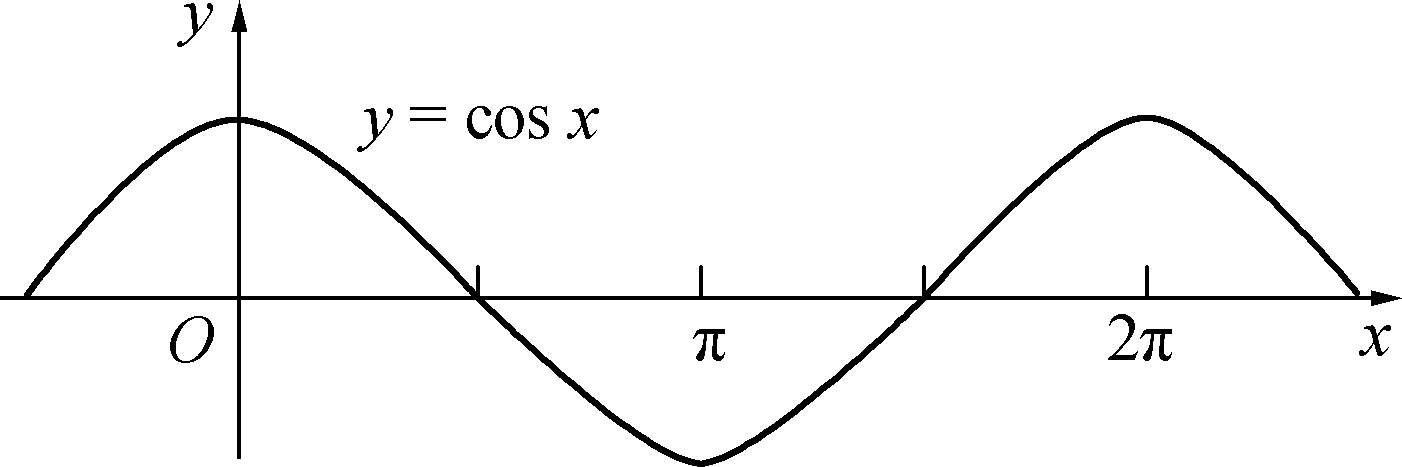
图1-3-2
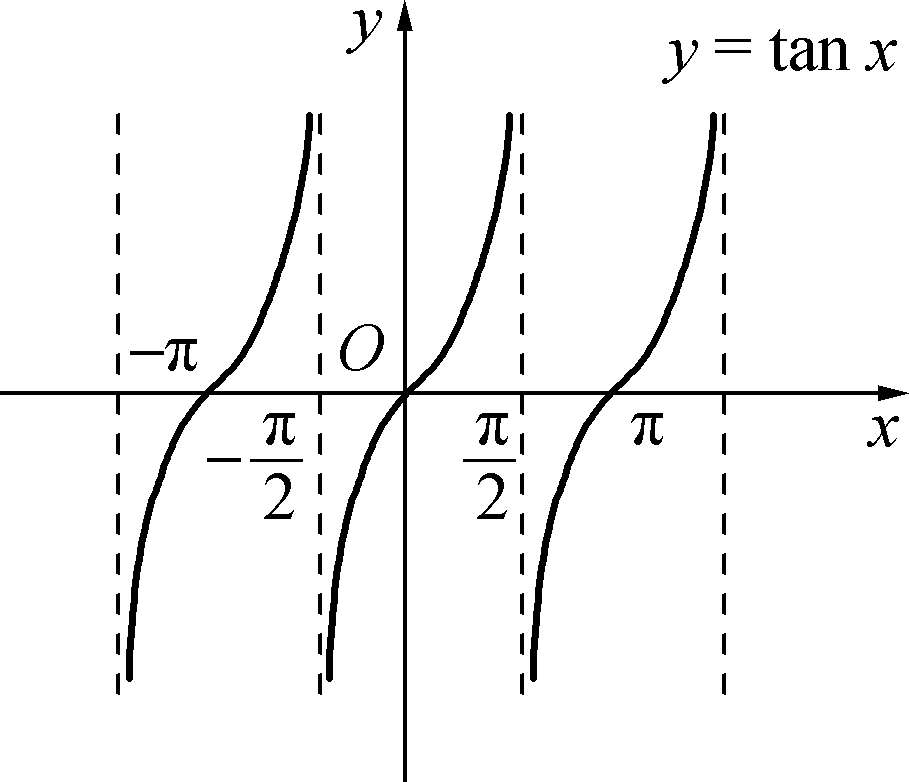
图1-3-3
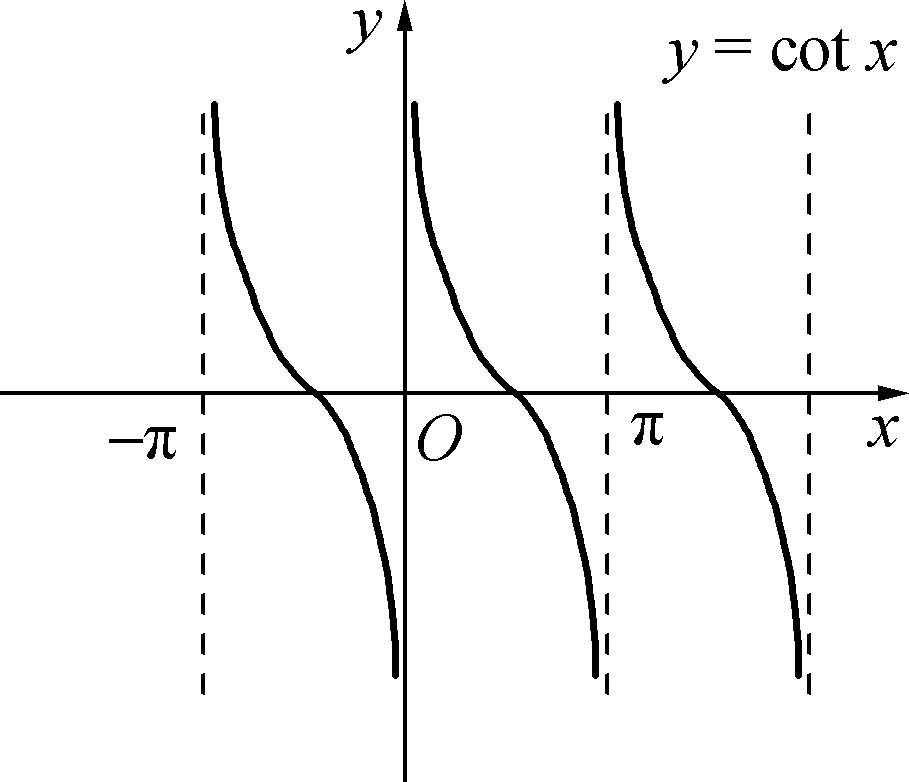
图1-3-4
此外,在后面的学习过程中,我们还要经常用到正割函数 y =sec x 和余割函数 y =csc x .因为
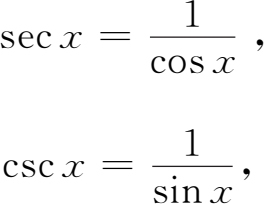
所以,我们常利用这种倒数关系来讨论正割、余割函数.它们都是以2π为周期的周期函数,并且在开区间
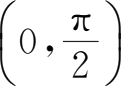 内都是无界函数.
内都是无界函数.
我们先来讨论正弦函数
y
=sin
x
的反函数.由于正弦函数
y
=sin
x
在其定义域(-∞,+∞)内不具有单调性,这时一定存在这样的一些
y
∈[-1,1],对于这其中的某一个
y
,有不止一个
x
∈(-∞,+∞)使关系式
y
=sin
x
成立.因此,正弦函数
y
=sin
x
在(-∞,+∞)内不存在反函数.若将讨论范围限制在闭区间
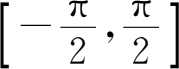 上,则
y
=sin
x
在
上,则
y
=sin
x
在
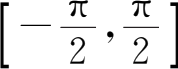 上单调递增,这时存在反函数,其反函数的定义域为[-1,1],值域是
上单调递增,这时存在反函数,其反函数的定义域为[-1,1],值域是
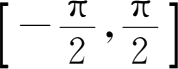 .
.
将
y
=sin
x
在区间
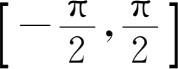 上的反函数称为反正弦函数
上的反函数称为反正弦函数
,记作 x =arc sin y ,按习惯写为 y =arc sin x .即正弦函数
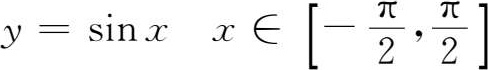
的反函数为反正弦函数
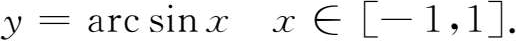
它们的图像关于直线 y = x 对称.反正弦函数在其定义域上单调增加,如图1-3-5所示.
类似地,将 y =cos x 在区间[0,π]上的反函数称为反余弦函数,记作 y =arc cos x x ∈[-1,1],反余弦函数在其定义域上单调减少,如图1-3-6所示.
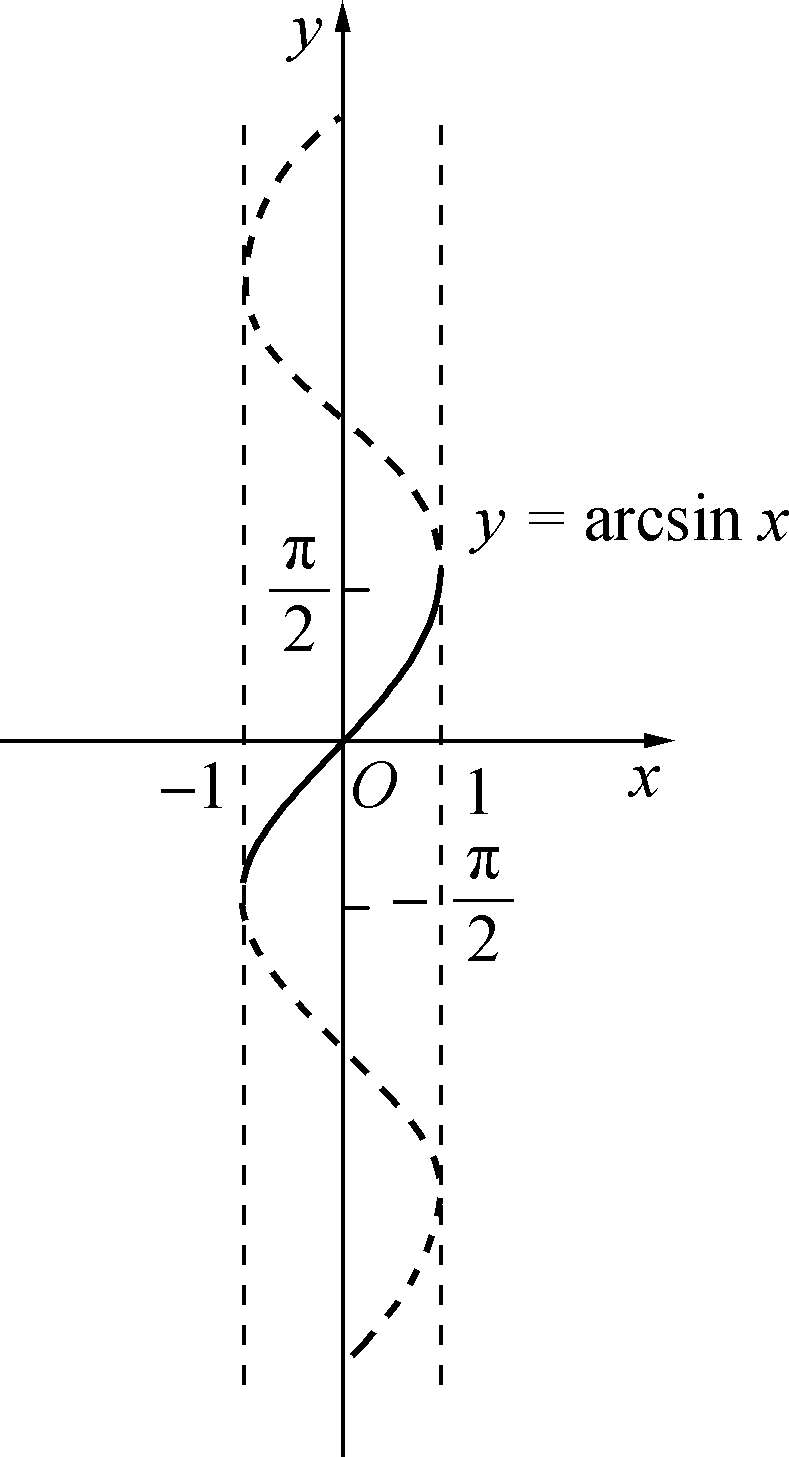
图1-3-5
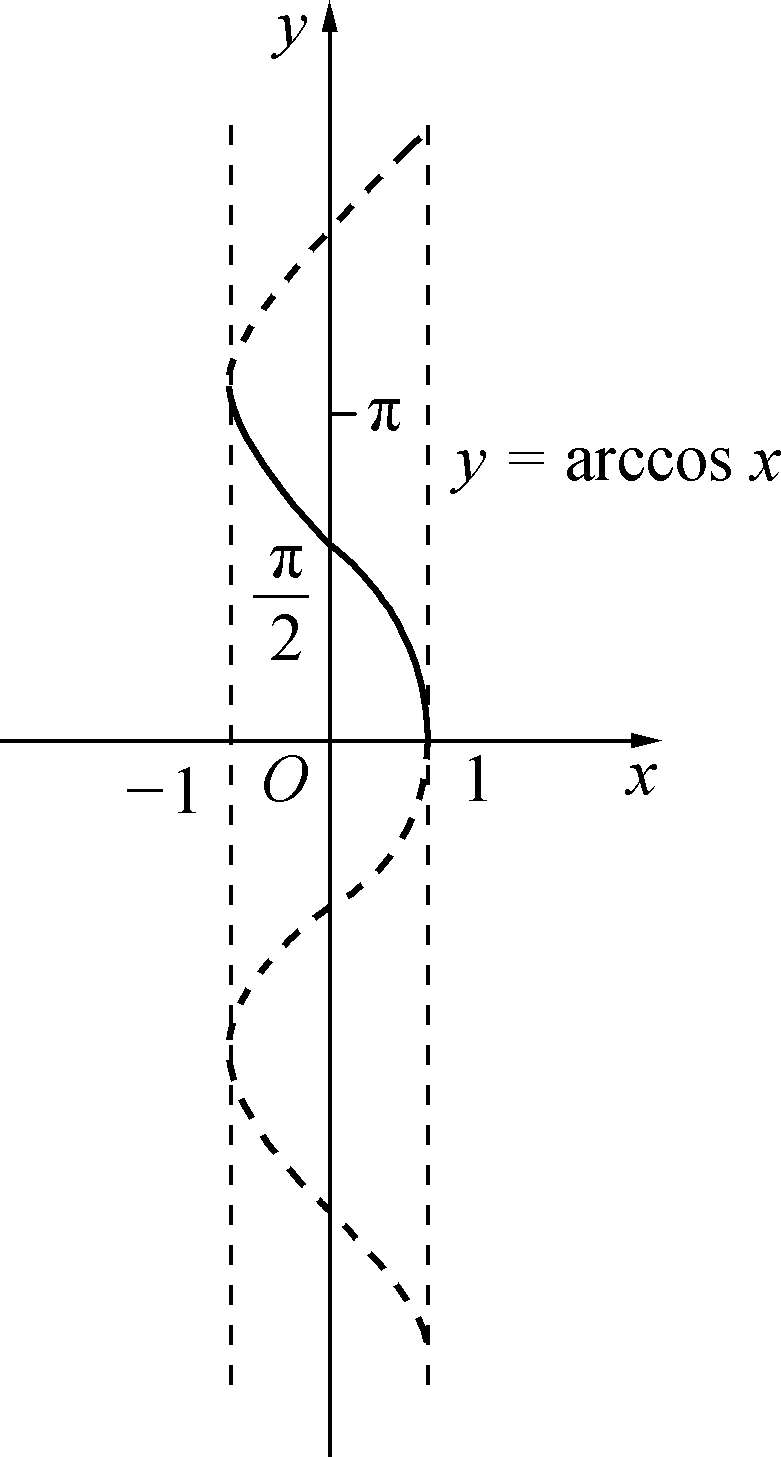
图1-3-6
将
y
=tan
x
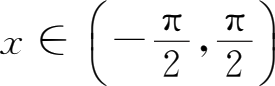 的反函数称为反正切函数,记作
y
=arc tan
x
x
∈(-∞,+∞),反正切函数在其定义域内单调增加,如图1-3-7所示.
的反函数称为反正切函数,记作
y
=arc tan
x
x
∈(-∞,+∞),反正切函数在其定义域内单调增加,如图1-3-7所示.
将 y =cot x x ∈(0,π)的反函数称为反余切函数,记作 y =arc cot x x ∈(-∞,+∞),反余切函数在其定义域内单调减少,如图1-3-8所示.
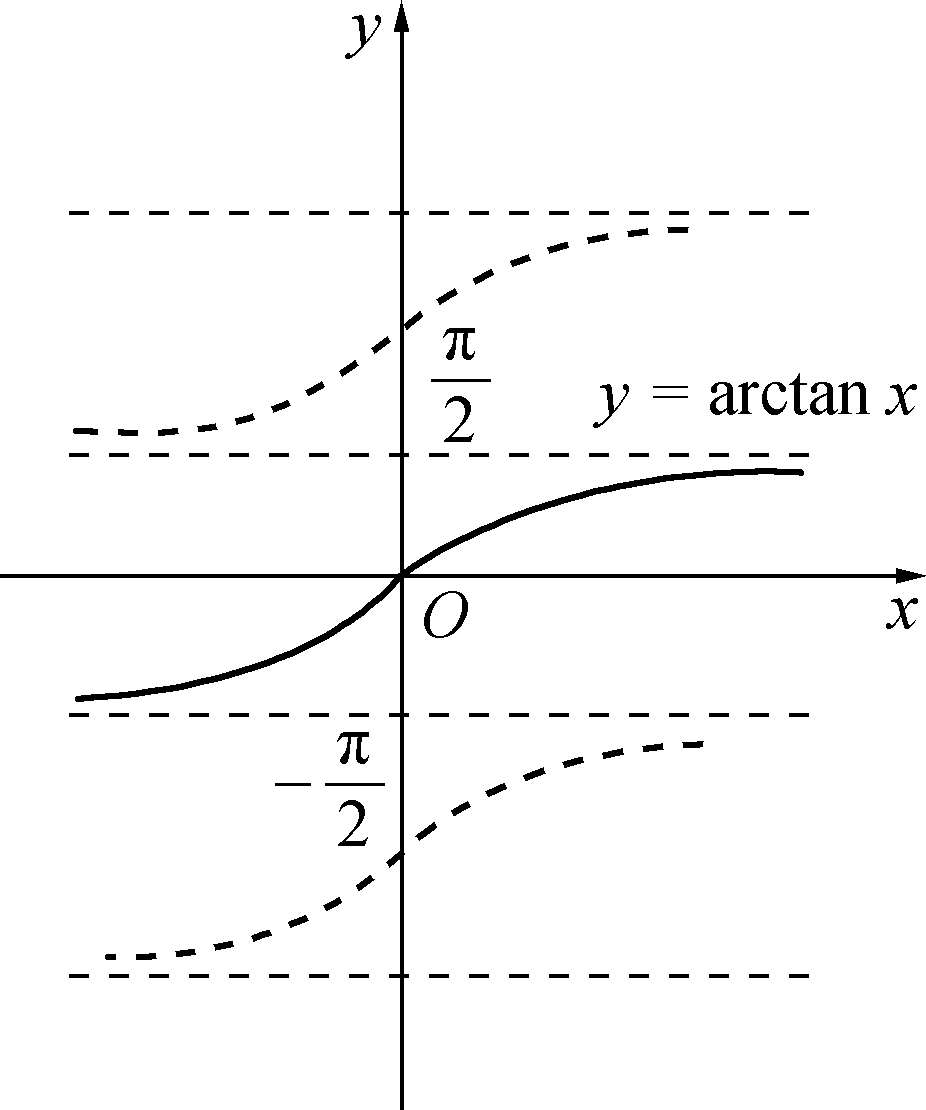
图1-3-7
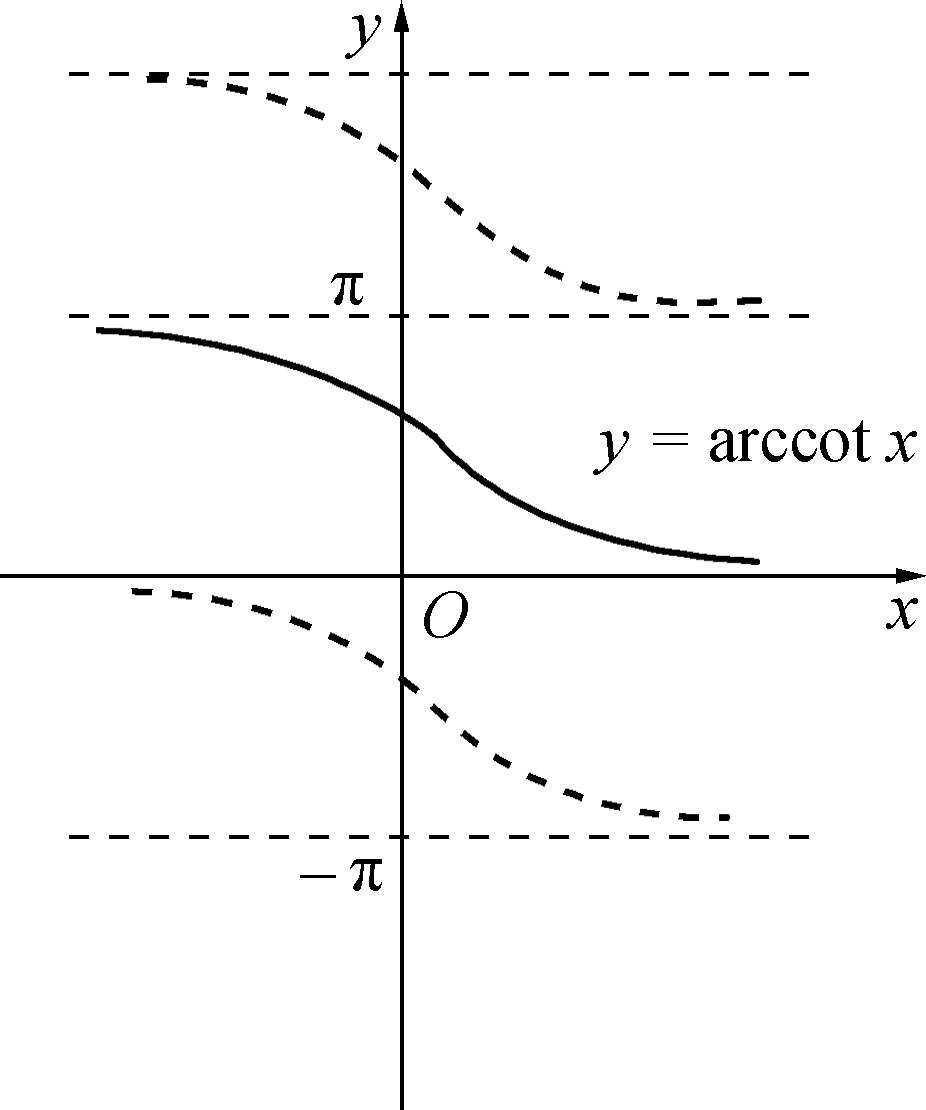
图1-3-8
反正弦函数、反余弦函数、反正切函数、反余切函数统称为反三角函数.
由定义可得下列一些基本关系:
(1)sin(arc sin x )= x , x ∈[-1,1];
(2)arc sin(sin
x
)=
x
,
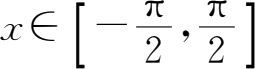 ;
;
(3)cos(arc cos x )= x , x ∈[-1,1];
(4)arc cos(cos x )= x , x ∈[0,π];
(5)tan(arc tan x )= x , x ∈(-∞,+∞);
(6)arc tan(tan
x
)=
x
,
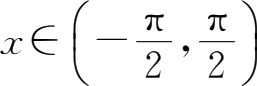 ;
;
(7)cot(arc cot x )= x , x ∈(-∞,+∞);
(8)arc cot(cot x )= x , x ∈(0,π).
另外,还可证明得到以下一些常用结论:
(1)arc cos(- x )=π-arc cos x , x ∈[-1,1];
(2)arc cot(- x )=π-arc cot x , x ∈(-∞,+∞);
(3)arc sin
x
+arc cos
x
=
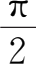 ,
x
∈[-1,1];
,
x
∈[-1,1];
(4)arc tan
x
+arc cot
x
=
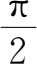 ,
x
∈(-∞,+∞).
,
x
∈(-∞,+∞).
【例1】 求下列函数的定义域:
(1) y =arc sin(- x 2 + x );
(2)
y
=arc tan
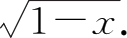
解 (1)因为-1≤- x 2 + x ≤1,
由- x 2 + x ≤1,可知对任意 x ∈(-∞,+∞)恒成立,
由
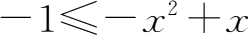 ,得
,得
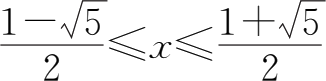 ,
,
所以定义域为
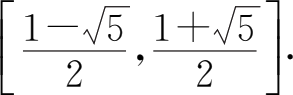
(2)因为1- x ≥0,可得 x ≤1,
所以定义域为(-∞,1].
【例2】 求下列各式的值:
(1)
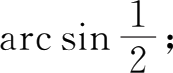
(2)
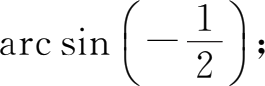
(3)arc tan
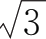 ;
;
(4)arc cot(-
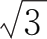 ).
).
解
(1)因为
 ,且
,且
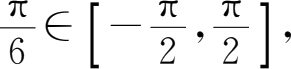
所以
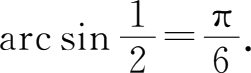
(2)
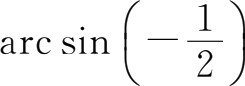 =-arcsin
=-arcsin
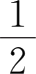 =-
=-
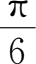 .
.
(3)因为
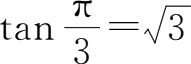 ,且
,且
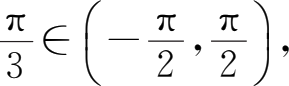
所以
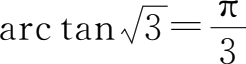 .
.
(4)因为
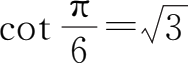 ,且
,且
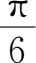 ∈(0,π),
∈(0,π),
所以
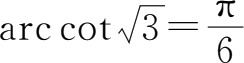 ,
,
所以arccot(-
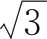 )=π-arccot
)=π-arccot
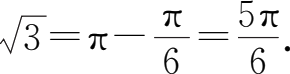
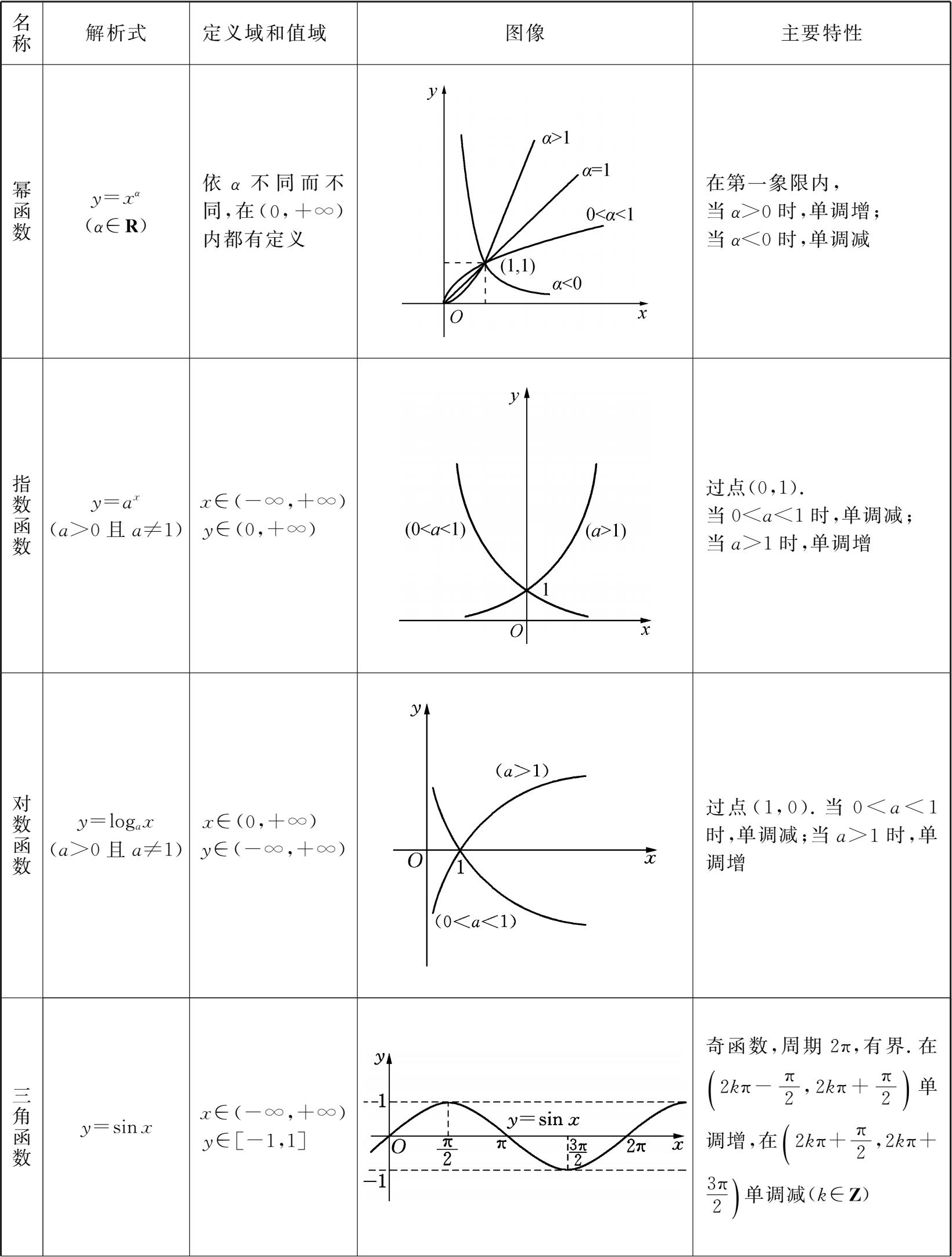
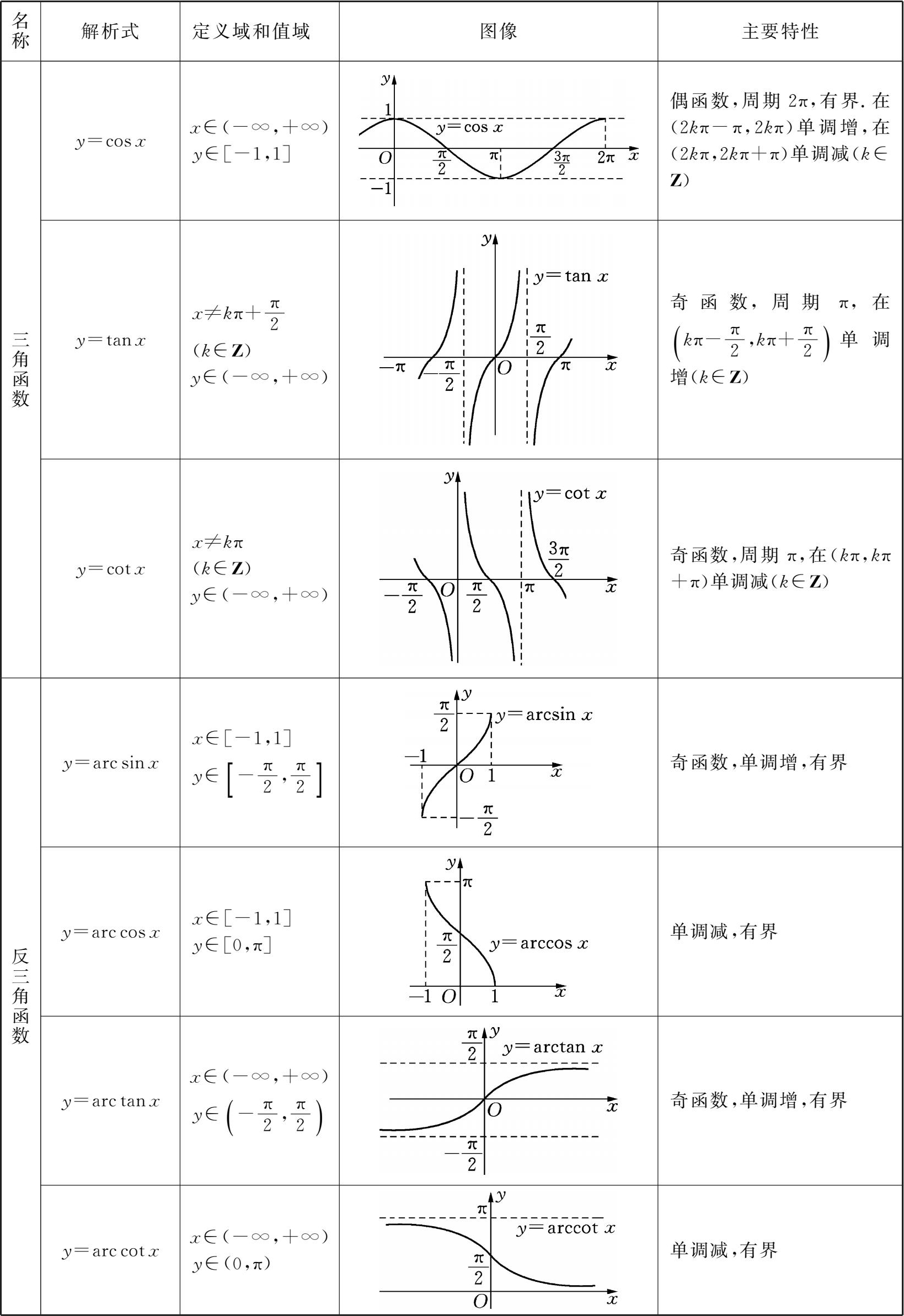
基本初等函数在数学学习中至关重要,必须熟练掌握.现把基本初等函数的图像及主要性质列于下表,以方便学习掌握.
(续表)
在实际问题中经常会出现这样的情形:一个变量依赖于另一个变量,而另一个变量又依赖于第三个变量.因此,第一个变量实际上可由第三个变量确定.
先举一个例子.设 y = u 2 , u =sin x ,以sin x 代替第一式中的 u ,得 y =sin 2 x .我们就说,函数 y =sin 2 x 是由 y = u 2 , u =sin x 复合而成的复合函数.
定义1.3.1 设函数 y = f ( u ),而 u = φ ( x ),且函数 u = φ ( x )的值域包含在函数 y = f ( u )的定义域内,那么通过 u 联系的 y 也是 x 的函数,我们称 y 是 x 的复合函数,记作 y = f [ φ ( x )],其中 u 叫作中间变量.
例如,由函数
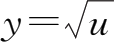 与
u
=
x
+5复合而成的复合函数为
与
u
=
x
+5复合而成的复合函数为
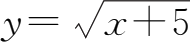 .为了使
u
的值域包含在
.为了使
u
的值域包含在
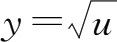 的定义域[0,+∞)之内,必须有
x
∈[-5,+∞),即复合函数
的定义域[0,+∞)之内,必须有
x
∈[-5,+∞),即复合函数
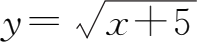 的定义域应为[-5,+∞).
的定义域应为[-5,+∞).
复合函数不仅可以由两个函数复合而成,也可以由两个以上的函数复合而成.例如,
y
=arc cos
u
,
u
=
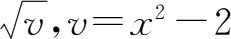 可以复合成复合函数
可以复合成复合函数
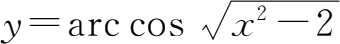 ,这里的
u
,
v
都称为中间变量.
,这里的
u
,
v
都称为中间变量.
显然,对于给定函数的复合,只要依次把中间变量的表达式代入函数中,就能形成只有一个自变量的复合函数.
应当指出,有些函数是不一定能复合成一个复合函数的.例如, y =arc sin u , u = x 2 +2在实数范围内就不能复合.因为对于任何 x 的值, u 的值都不在 y =arc sin u 定义域[-1,1]的范围内.
另一方面,我们也可把一个较复杂的函数看成由几个简单函数复合而成.为方便讨论,有时需要对复合函数进行分解.复合函数的分解,应当遵循“由表及里、逐层分解”的原则.
【例3】 分解函数 y =cos 3 (2e x -3)成简单函数.
解 把这个函数写成 y =[cos(2e x -3)] 3 ,因此令 u =cos(2e x -3),有 y = u 3 .而对于 u =cos(2e x -3),令 v =2e x -3,有 u =cos v .函数 v =2e x -3是简单函数,不需再分解了.这样, y =cos 3 (2e x -3)可分解为 y = u 3 , u =cos v , v =2e x -3.
【例4】 指出下列函数是由哪些函数复合而成的:
(1) y =(cos x ) 4 ;
(2) y =e -x ;
(3)
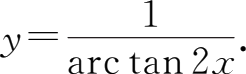
解 (1) y =(cos x ) 4 是由 y = u 4 , u =cos x 复合而成的;
(2) y =e -x 是由 y =e u , u =- x 复合而成的;
(3)
 是由
是由
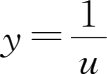 ,
u
=arc tan
v
,
v
=2
x
复合而成的.
,
u
=arc tan
v
,
v
=2
x
复合而成的.
复合函数的分解是研究复杂函数的基础,是经常使用的有效方法.
定义1.3.2 由基本初等函数经过有限次的四则运算和有限次的复合,并且能够用一个解析式表示的函数称为初等函数.
例如,
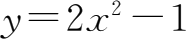 ,
y
=sin
,
y
=sin
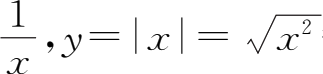 等函数都是初等函数,而分段函数
等函数都是初等函数,而分段函数
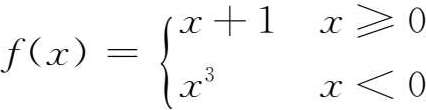
不是初等函数,因为它在定义域内并不是用一个解析式表示的.