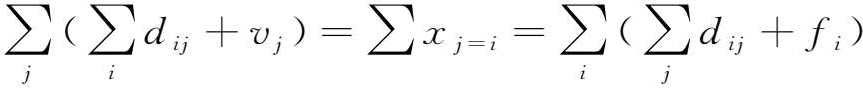基本的投入产出模型通常利用所观测的特定地理区域(国家、省、市、县等)的经济数据来建模。它所关注的是一组产业的活动,这些产业在生产每个产业自身产出的过程中,既生产货物(产出),又消耗来自其他产业的货物(投入)。在实际中,所涉及的产业数目可能从几个,到百个甚至上千个。例如,一个可以被冠以“制造业产品”的产业部门,同样也可能被分解为众多不同的特定产品。
投入产出模型所赖以建立的这些基本信息包含在一张产业间交易表中,表中的行描述的是生产者的产出在整体经济中的分配,表中的列描述的是某一特定产业在生产其产出时所需的各种投入的构成。这些物品的产业间交易构成了表2-1中所示的表格的阴影部分。附加的那些列,标记为最终需求,记录的是各个部门向其为之生产的最终市场的销售,如个人消费购买以及向联邦政府的销售。例如,电力既向其他部门的企业销售,用于生产中的投入(产业间交易),也向常住消费者销售(最终需求销售)。附加的那些行,标记为增加值,记录生产中的其他(非产业的)投入,如劳动、资本消耗、企业间接税和进口。
为了较好地把握投入产出的基本模型框架,我们需要注意三个环节:
一是将产出区分为中间产品与最终产品,投入区分为中间投入与初始投入,进而在这一对概念的基础上掌握投入产出表的基本结构与平衡关系;
二是直接消耗系数的引入,以及从直接消耗系数到完全消耗系数;
三是基于直接消耗系数与完全消耗系数的建模。
我们正是以这样一个思路对投入产出表的基本结构、投入产出分析中的基本概念与模型做简要的介绍。对投入产出表的基本结构的了解,可以从投入与产出这一对概念开始。生产过程就是以一定的投入,采用某种技术转换为产出的过程。在投入产出表中,列向表示生产过程中的投入及其构成,而行向则表示产品产出及其分配使用去向。投入产出对整个国民经济以不同产品的生产进行部门分类,进而在产业联系之中反映国民经济的全貌。
投入产出中进一步把投入分为中间投入和初始投入,产出分为中间产品与最终产品。首先,中间产品和最终产品是如何区分的呢?区分的标准很简单,就是看在所考察的期间是否再回到生产过程中去。如果在本期内不再进入生产过程,那么就称这类产品为最终产品。中间产品则是本期生产出来,再次进入生产过程。
表2-1 投入产出交易表
我们不难从实际的生产活动中观察到,各产业部门在产出其产品及服务时需要使用各种原材料和消耗能源动力,还需要使用各种工具设备以及需要劳动力付出劳动。例如,在图2-1所示的种植业的生产活动中,需要播撒种子,施以化肥,以及接受技术服务,等等。同时,也需要使用各类农机具,当然还需要农民付出劳动以从事生产。这里,我们把产业部门在其产出产品及服务的生产活动中对原材料、工具设备以及劳动力等的使用统称为投入。

图2-1 第一产业(种植业)产出中的各种投入及其结构
我们可以通过考察这些投入的差异并加以理论归纳,将其区分为中间投入和初始投入两大类。
(1)中间品和中间投入(中间消耗)。
首先,我们可以区分出有一类投入是来自各产业部门所提供的产品及服务,如图2-1所示种植业中使用的种子、化肥和技术服务以及农机具等。
进一步考察又可以发现,这类投入还可以区分成两类:一类如图2-1种植业中的种子、化肥和技术服务等。此类投入在形成产出的同时被完整地消耗掉,其功能也就在于在产出时被完整地消耗掉,因而其价值便也在形成产出时全部地进入该部门的产出价值之中。我们把这类投入从产品角度称为中间品,进而将此类投入称作中间投入,也称中间消耗。
(2)初始要素和初始投入(增加值)。
另有一类投入与上述中间投入不同,如图2-1所示的种植业中对农机具的使用等。虽然这类投入同样来自各产业部门所提供的产品及服务,但与中间投入不同的是,此类投入在形成产出时只是被部分地消耗,并且其功能也不在于在生产中消耗掉自身,因而其价值在形成产出时只是部分地、以折旧等方式进入产出价值之中。我们把此类投入从产品的角度称为资本品,进而将此类投入称为资本投入。
显然,从价值层面来说,产出价值中的资本投入的价值不等于资本品自身的价值。另外,我们把劳动力为生产所付出的劳动称为劳动投入,虽然就付出的劳动而言在形成产出时即被完整地消耗,其价值全部地进入产出价值之中,但就提供了这些劳动的劳动力而言,其功能与资本品一样也显然不在于在生产中消耗掉自身,进而,如同产出价值中的资本投入的价值不等同于资本品自身的价值一样,产出价值中的劳动投入的价值也不等同于劳动力自身的价值。
我们把劳动力和资本品称为初始要素,把资本投入和劳动投入称为初始投入,也称初始消耗。从其价值层面来说初始投入对应着经济学中的增加值,因此也直接称为增加值投入。
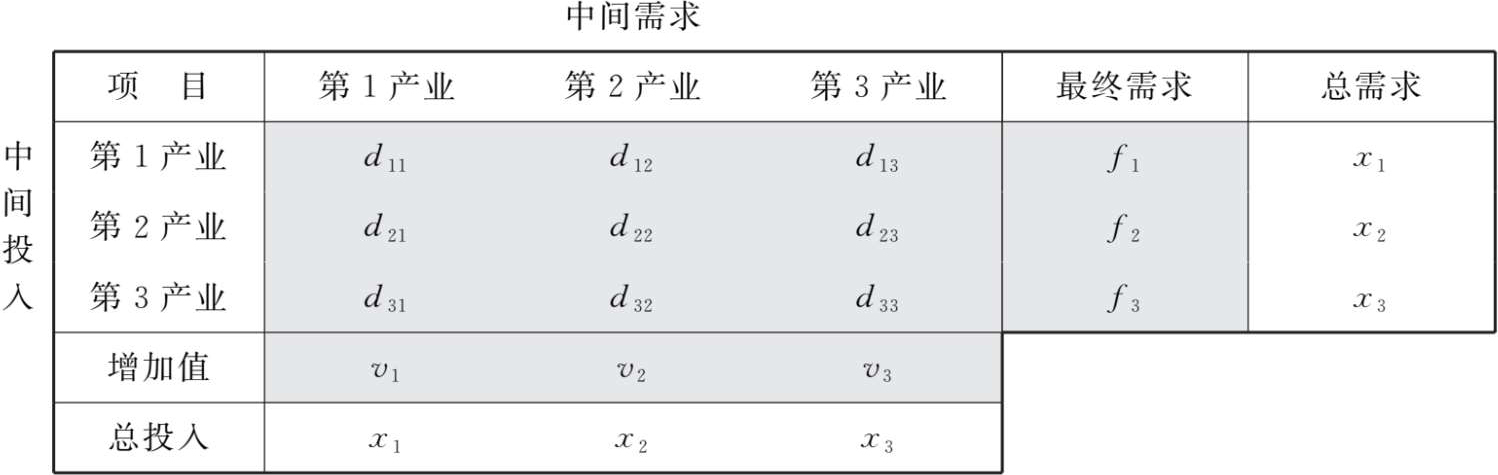
我们对以上的观察和理论归纳进行一个一般性的整理。首先,我们用 i 和 j 来表示产业部门;用 d ij 来表示中间投入,即 j 产业产出中投入的 i 产业中间品;用 v j 来表示 j 产业产出中投入的初始投入,即增加值。
接下来,如表2-2所示,我们将其适用于全部产业。于是,我们便得到了一个归纳各产业部门各项投入的一个一般性的矩阵式框架。
表2-2 归纳各产业产出中的各种投入的一般框架

我们将该框架中各产业的中间投入称为中间投入矩阵或中间消耗矩阵,将各产业的初始投入称为初始投入矩阵或增加值矩阵。显然, d ij 是一个理论界定,并不意味着现实中一定对应有数值。例如,第3产业的生产活动中一般不会有来自农产品的中间投入,则 d 13 =0。
在对关于各产业部门生产活动中的各种投入进行观察的基础上,来考察各部门产出的使用去向,显然可以基于其是否进入各产业部门形成当期产出的生产过程之中而区分并归纳出如下两大使用去向。
(1)中间使用(中间需求)。
一个使用去向是作为中间品进入该经济体中各产业形成当期产出的生产过程之中成为对方的中间投入,我们称为中间使用领域,或者从使用方的角度称为中间需求领域。例如,图2-2所示的种植业的产出(如玉米)的一部分被作为饲料原料而进入第2产业中的饲料加工业的生产过程中成为其中间投入等。

图2-2 第1产业(种植业)产出的使用去向及其结构
(2)最终使用(最终需求)。
另一个使用去向是作为最终品而进入消费、资本形成以及出口等领域,我们称为最终使用领域,或者从使用方的角度称为最终需求领域。此类使用去向的共同点在于,其进入的不是该经济体中各产业形成当期产出的生产过程之中,或者是生产活动以外的领域,如消费;或者是关系到后期产出的领域,如广义的资本形成;又或者是其他经济体,如出口。
我们对以上的观察和归纳进行一个一般性的整理。首先,同样用 i 和 j 来表示部门;用 d ij 来表示中间需求,即 j 产业对 i 产业产出的中间需求;用 f i 来表示对 i 产业产出的最终需求。接下来,如表2-3所示,我们将其适用于全部产业。于是,我们便得到了一个归纳各产业产出的各类使用去向的一个一般性的矩阵式框架。
表2-3 归纳各产业产出的各使用去向的一般框架

我们将该框架中各产业的中间使用称为中间使用矩阵或中间需求矩阵,将各产业的最终使用称为最终使用矩阵或最终需求矩阵。
实际上,中间投入和中间需求归纳出来的是同一个由 d ij 组成的正方矩阵。我们称其为中间投入—中间需求矩阵。中间投入—中间需求的正方矩阵特点为构建一个整合了各产业的总投入和总使用的核算框架提供了着眼点。如表2-4所示,在中间投入—中间需求正方矩阵的下方衔接各产业的初始投入矩阵,在其右侧衔接各产业的最终需求矩阵,就形成了一个由这三个矩阵整合而成的核算表框架。这就是投入产出表的基本核算框架。
表2-4 投入产出表的基本框架结构
可以看出,投入产出表通过其矩阵布局,巧妙地在同一个核算表框架里完整地整合了各产业产出中的各种投入以及各项使用去向这两个方面的内容。
实物型投入产出表与价值型投入产出表在框架上并没有大的不同。区别在于:价值型投入产出表记录的是以货币为单位的价值流量,如元、万元等;实物型投入产出表记录的则是以实物为单位的实物流量,如吨、个等。或者不妨说,价值型投入产出表是关于“产值”的表,实物型投入产出表是关于“产品”的表。显然,实物型投入产出表从“物”的层面反映投入产出关系;价值型投入产出表则从“价值”或者至少是“货币值”的层面反映投入产出关系。后者基于其上述特点而在经济学分析中更为常用。
上面介绍的投入产出表基本核算框架是封闭情形下的,没有考虑开放条件下的进口情况。如果在投入产出表中考虑进口,则应区分中间投入—中间需求矩阵中的国产品
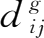 和进口品
和进口品
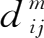 ,以及区分最终需求矩阵中的国产品
,以及区分最终需求矩阵中的国产品
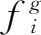 和进口品
和进口品
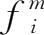 。对此有两种统计及核算方式,分别称为进口竞争型投入产出表和非进口竞争型投入产出表。
。对此有两种统计及核算方式,分别称为进口竞争型投入产出表和非进口竞争型投入产出表。
(1)进口竞争型投入产出表。
表2-5表示了进口竞争型投入产出表的核算特点。首先,进口竞争型投入产出表中不识别中间投入—中间需求矩阵以及最终需求矩阵中的国产品和进口品。也就是说,表中两矩阵中的统计量是进口量和国产量合计在一起的。其次,表中统计进口总量,并通过将其从横向上整体加以扣除以保持总需求与国内总产出的平衡关系。
表2-5 进口竞争型投入产出表
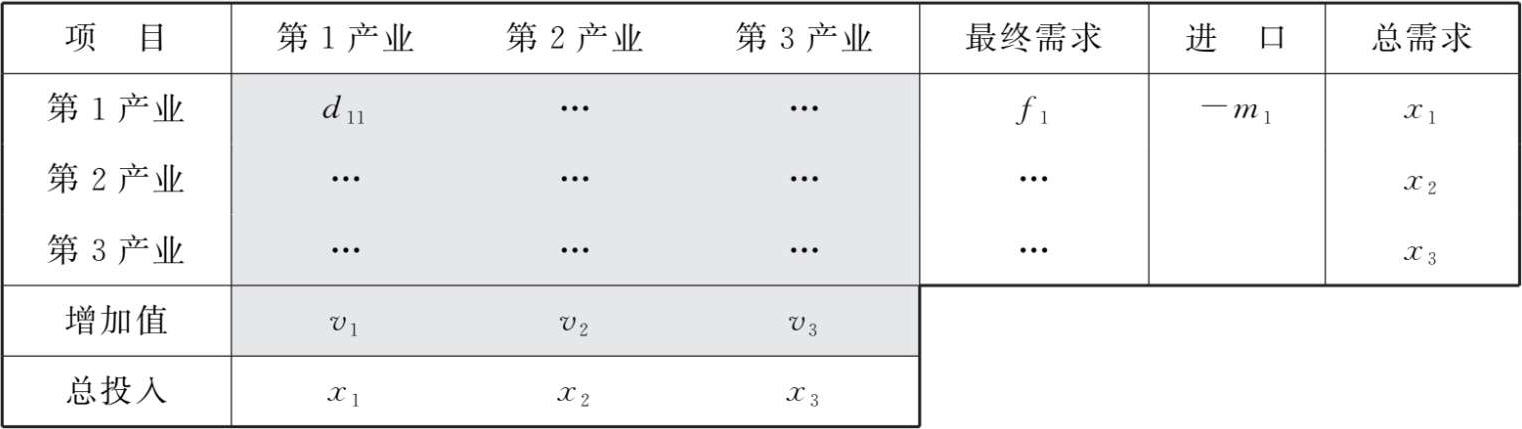
其中,
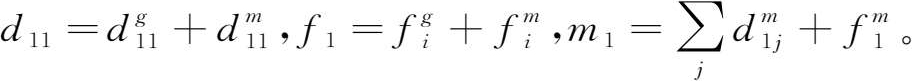
(2)非进口竞争型投入产出表。
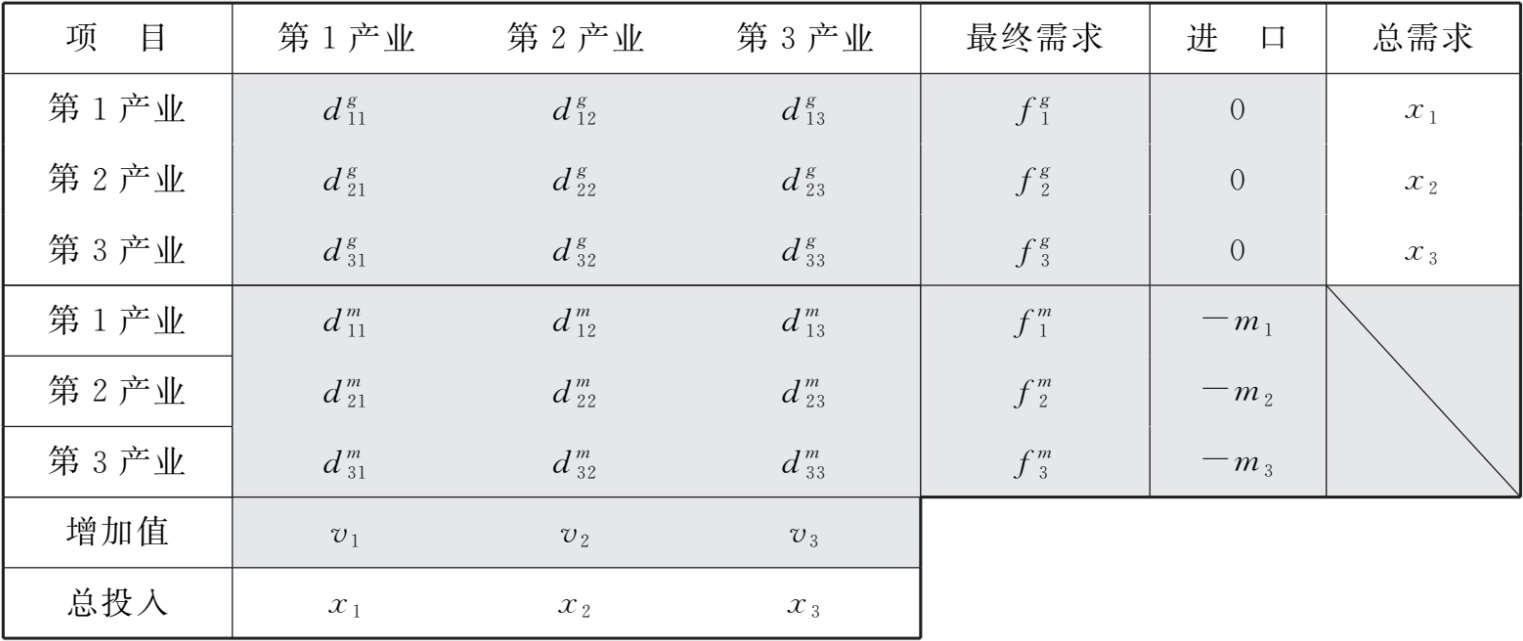
表2-6表示非进口竞争型投入产出表的基本核算框架。其特点是对国产品的中间需求和最终需求以及对进口品的中间需求和最终需求分列出来并独自核算。显然,该表在对国产品和进口品的使用情况方面提供了更多周到的信息。
表2-6 非进口竞争型投入产出表
首先,在价值型投入产出表的各产业列中,存在如下产业总投入与其总产出之间的价值等量关系,同时也是价值型投入产出表中的一个核算关系,即:
产业总投入(中间投入+初始投入)价值=产业总产出价值
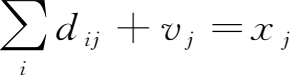
其次,在价值型投入产出表的各产业行中,存在如下产业产出与其使用去向之间的价值等量关系,同时也是投入产出表中的另一个核算关系,即:
产业总产出价值=产业总需求(中间使用+最终使用)价值
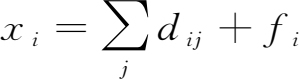
综合上述两个等量关系,在投入产出表中各产业的价值流量数据之间存在如下“三边等价”的价值等量关系,即:
产业总投入价值=产业总产出价值=产业总需求价值
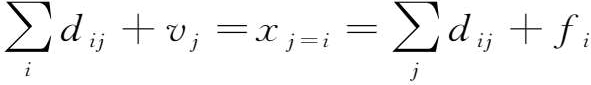
显然,由于上述等量关系对各个产业均成立,因此在将各产业加总的全社会层面上自然有如下等量关系,即:
全社会总投入价值=全社会总产出价值=全社会总需求价值