




熟悉经济结构分析的各种系数,掌握经济结构分析的基本方法。
计算最终需求产品结构系数、最终需求分配结构系数、生产诱发额、生产诱发系数、生产依存度、增加值诱发额和增加值诱发系数。
2学时。
Excel软件。
系数分为四组:最终需求产品结构系数;最终需求分配结构系数;生产诱发额、生产诱发系数、生产依存度;生产诱发额、增加值诱发额、增加值诱发系数。
假设已知的消费向量为 F C ;投资向量为 F I ;出口向量为 F E ;进口向量为 F M ;最终使用向量为 F 。
(1)开机进入Excel。
(2)打开19部门投入产出表,以某地区2022年19部门投入产出表为例,分析整理得到该地区2022年投入产出最终使用表,在此基础上进行相关投入产出分析的计算。
分析最终需求的产品结构就是分析最终需求的产品构成,最终需求的产品结构也称为列结构,其系数定义如下:
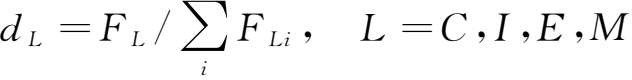
最终需求的产品结构系数表示的是某种最终使用产品占最终使用总量的比例。根据定义得到实验表4-1-1。
实验表4-1-1 某地2022年最终使用产品结构系数表
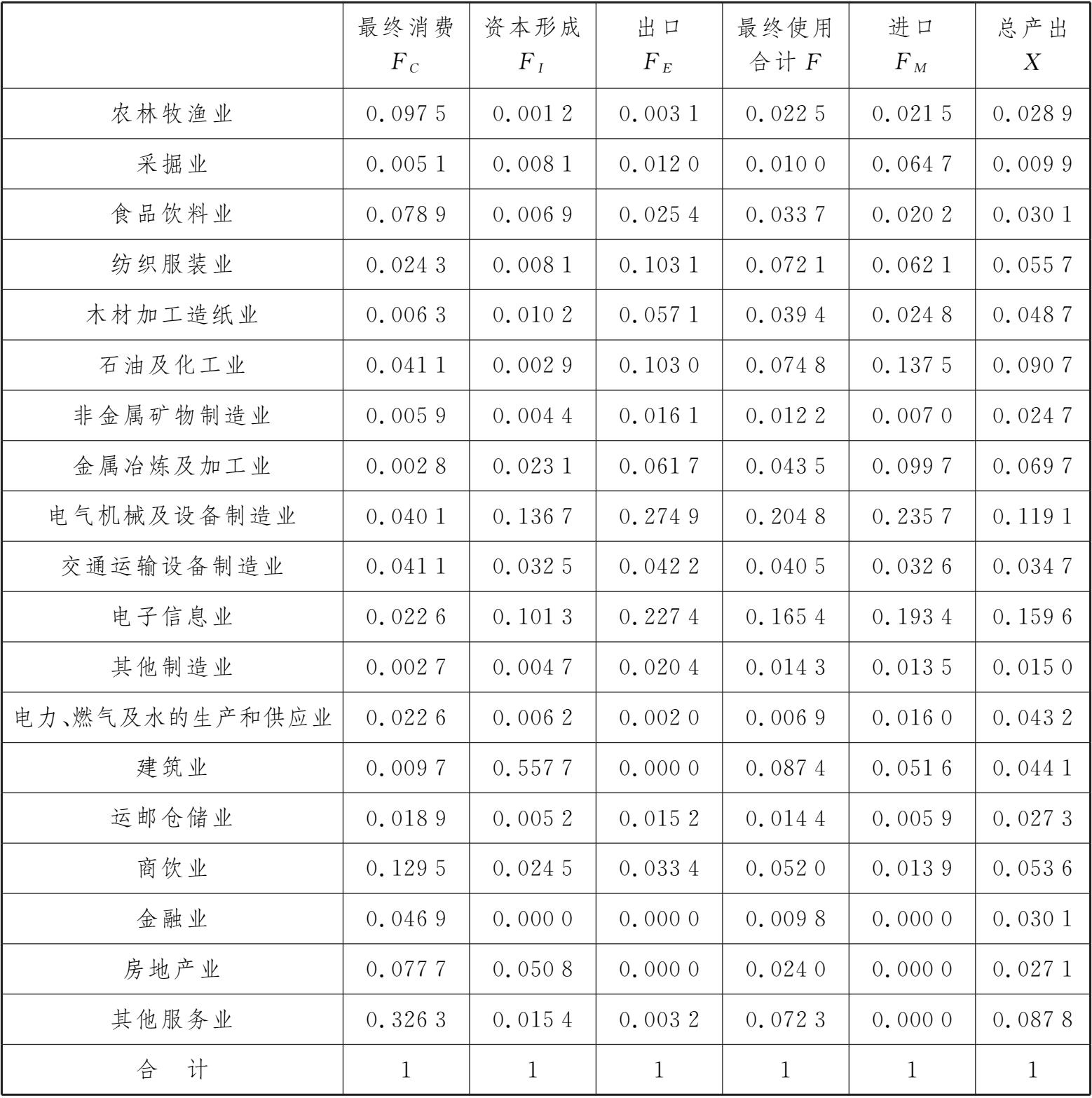
从最终需求产品结构系数可以看出:用于最终消费的依次主要是其他服务业、商饮业、农林牧渔业、食品饮料业、房地产业和金融业;用于资本形成的最主要是建筑业,其次是电气机械及设备制造业、电子信息业;用于输出的最主要是电气机械及设备制造业、电子信息业和纺织服装业;对于输入产品而言,主要是石油及化工业、电气机械及设备制造业和电子信息业。
分析最终需求的分配结构就是分析最终需求的项目构成,最终需求的分配结构也称行结构,其系数定义如下:
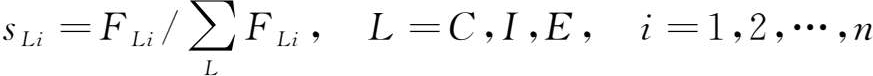
最终需求的分配结构系数表示的是某部门某项最终使用产品占该部门最终使用总量的比例。根据定义计算得到实验表4-1-2。
实验表4-1-2 某地区2022年最终使用分配结构系数表
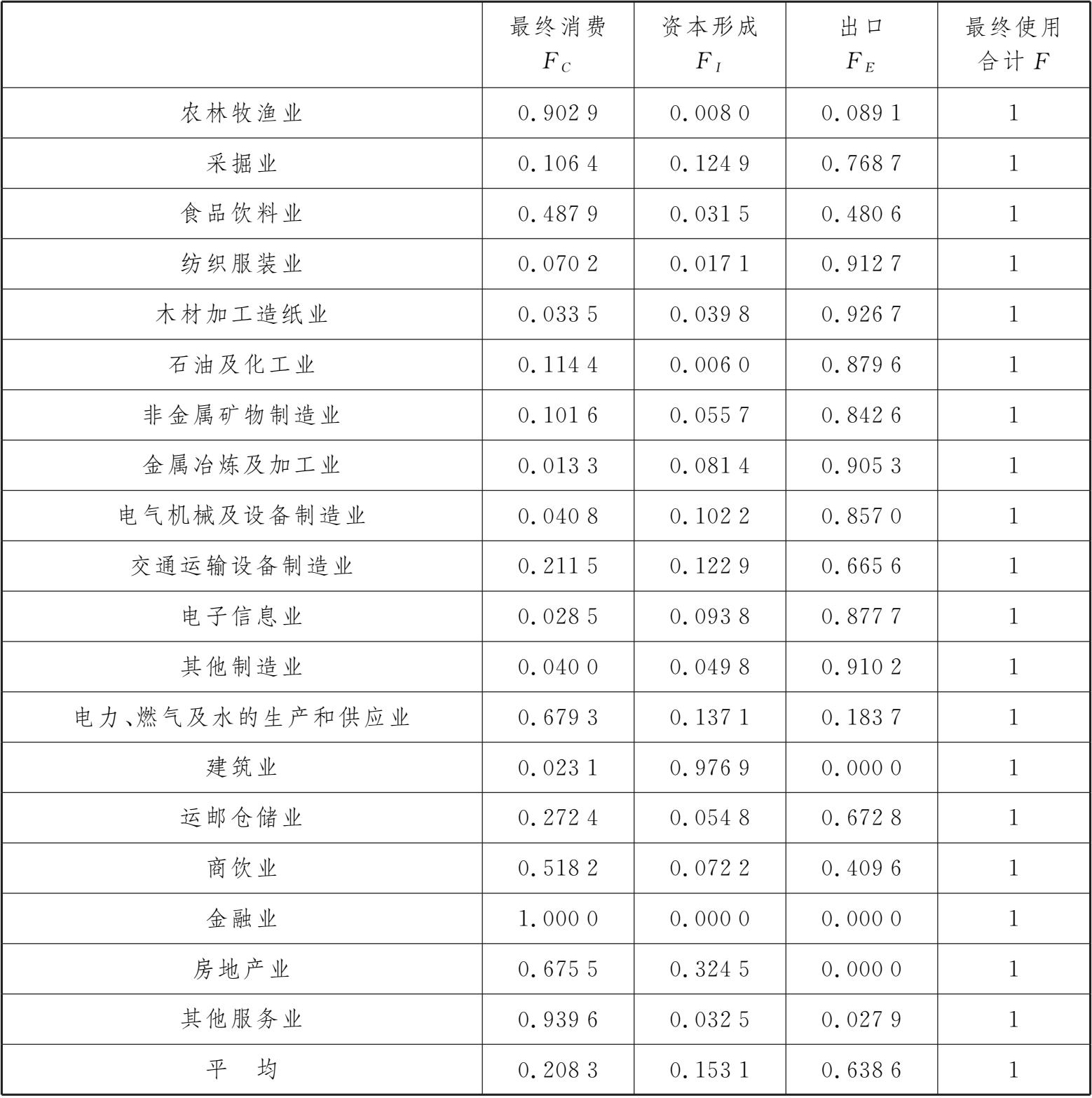
从最终需求分配结构系数可以看出:农林牧渔业,电力、燃气及水的生产和供应业,商饮业及其他服务业,金融业房地产业其最终需求主要用于最终消费;建筑业其最终需求主要用于资本形成;采掘业、纺织服装业、木材加工造纸业、石油及化工业、非金属矿物制品业、金属冶炼及加工业、电气机械及设备制造业、交通运输设备制造业、电子信息业、运邮仓储业其最终需求主要用于输出。
最终需求是影响生产的主要因素,最终需求决定了总产出。利用列昂惕夫逆矩阵可对各产业的生产诱发额和生产诱发系数进行分析。
(1)生产诱发额的计算
第一步,打开19部门投入产出表,计算A,
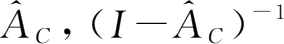 ,
,
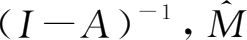 ,
,
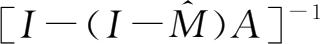 。
。

计算
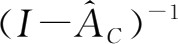 :计算
:计算
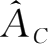 ,在要放
,在要放
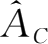 的地方标上
的地方标上
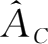 ,选取一个19行19列的新区域,输入“0”,然后按Ctrl+Enter键,最后把对应的对角元素改为
,选取一个19行19列的新区域,输入“0”,然后按Ctrl+Enter键,最后把对应的对角元素改为
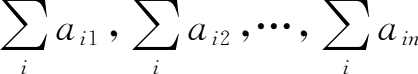 ,即逐个求得对角元素。第一个对角元素为矩阵
A
的第一列求和,第二个对角元素为矩阵
A
的第二列求和,依此类推,求出19个对角元素即得矩阵
,即逐个求得对角元素。第一个对角元素为矩阵
A
的第一列求和,第二个对角元素为矩阵
A
的第二列求和,依此类推,求出19个对角元素即得矩阵
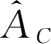 。计算
。计算
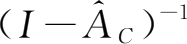 ,要在放矩阵
,要在放矩阵
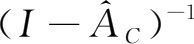 的区域的上面标
的区域的上面标
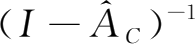 ,选取一个19行19列的新区域,单击工具栏上的函数工具,选中数学与三角函数中的MINVERSE函数(矩阵求逆矩阵),选取矩阵
,选取一个19行19列的新区域,单击工具栏上的函数工具,选中数学与三角函数中的MINVERSE函数(矩阵求逆矩阵),选取矩阵
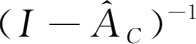 ,然后按Ctrl+Shift+Enter键就可得到矩阵
,然后按Ctrl+Shift+Enter键就可得到矩阵
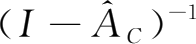 。
。
计算对角阵
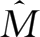 :先求出进口
F
M
,选取一个19行19列的新区域,输入“/”,选取19部门的总需求(总产出+进口-出口)行,然后按Ctrl+Shift+Enter键,那么就可以得到过渡矩阵,在要放矩阵
:先求出进口
F
M
,选取一个19行19列的新区域,输入“/”,选取19部门的总需求(总产出+进口-出口)行,然后按Ctrl+Shift+Enter键,那么就可以得到过渡矩阵,在要放矩阵
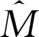 的右边标
的右边标
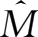 ,选取一个19行19列的新区域,单击工具栏上的函数工具,选中数学三角函数中的MMULT函数(矩阵相乘函数),选取单位矩阵
I
,再选取过渡矩阵,然后按两次Ctrl+Shift+Enter键,就可以得到
,选取一个19行19列的新区域,单击工具栏上的函数工具,选中数学三角函数中的MMULT函数(矩阵相乘函数),选取单位矩阵
I
,再选取过渡矩阵,然后按两次Ctrl+Shift+Enter键,就可以得到
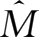 矩阵。
矩阵。
同理可计算(
I
-
A
)
-1
,
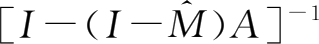 。
。
第二步,根据:
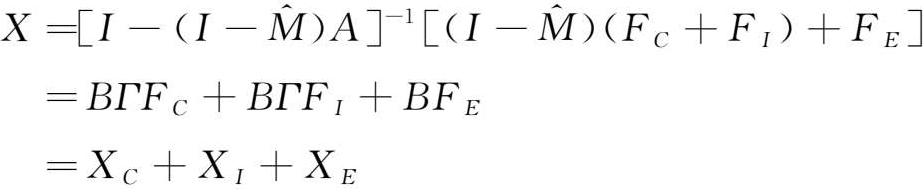
式中,
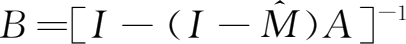 ,
,
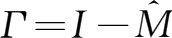 ,
X
C
=
BΓF
C
,
X
I
=
BΓF
I
,
X
E
=
BF
E
,
X
C
,
X
I
,
X
E
分别表示最终消费
F
C
、资本形成
F
I
、出口
F
E
诱发出的生产额向量。
,
X
C
=
BΓF
C
,
X
I
=
BΓF
I
,
X
E
=
BF
E
,
X
C
,
X
I
,
X
E
分别表示最终消费
F
C
、资本形成
F
I
、出口
F
E
诱发出的生产额向量。
计算矩阵
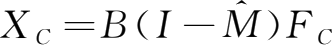 ,
,
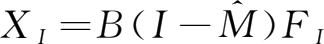 ;选择19行和2列新区域,单击工具栏上的函数工具,选中数学与三角函数中的MMULT函数(矩阵相乘函数),选取矩阵
;选择19行和2列新区域,单击工具栏上的函数工具,选中数学与三角函数中的MMULT函数(矩阵相乘函数),选取矩阵
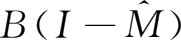 ,再选取矩阵
F
C
+
F
I
,然后按两次Ctrl+Shift+Enter键,就可得到矩阵
X
C
+
X
I
;选取19行和1列新区域,单击工具栏上的函数工具,选中数学与三角函数中的MMULT函数(矩阵相乘函数),选取矩阵
B
,再选取矩阵
F
E
列矩阵,然后按两次Ctrl+Shift+Enter键,就可得到矩阵
X
E
;最后对
X
C
,
X
I
,
X
E
分部门求和,即得各生产诱发总额。计算得到该地区2022年生产诱发总额,见实验表4-1-3。
,再选取矩阵
F
C
+
F
I
,然后按两次Ctrl+Shift+Enter键,就可得到矩阵
X
C
+
X
I
;选取19行和1列新区域,单击工具栏上的函数工具,选中数学与三角函数中的MMULT函数(矩阵相乘函数),选取矩阵
B
,再选取矩阵
F
E
列矩阵,然后按两次Ctrl+Shift+Enter键,就可得到矩阵
X
E
;最后对
X
C
,
X
I
,
X
E
分部门求和,即得各生产诱发总额。计算得到该地区2022年生产诱发总额,见实验表4-1-3。
实验表4-1-3 某地区2022年最终使用生产诱发额表 单位:万元
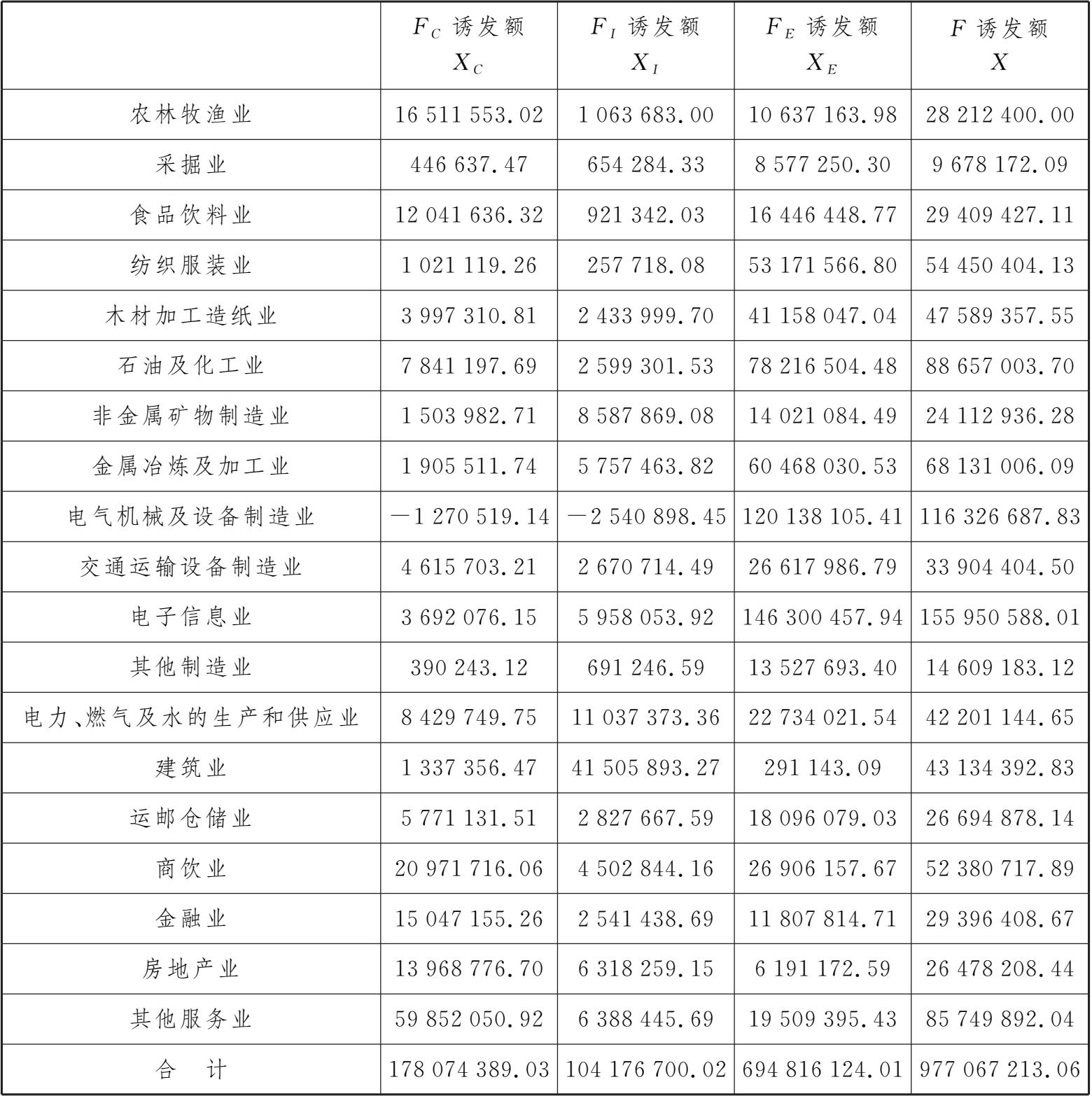
生产诱发额是指对于各项最终需求量,由产业间的波及效应所激发的全部生产额。生产诱发系数是指某项最终使用若增加1单位,则相应的产出总量将要增加多少单位。
(2)生产诱发系数
生产诱发系数是诱发生产额与相应的最终需求额合计之比,其含义是某项最终使用若增加一个单位,则相应的产出总量将要增加多少个单位。生产诱发系数定义如下:
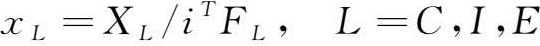
式中, x C , x I , x E 分别表示最终消费、资本形成、出口的生产诱发系数向量; i T =(1,1,…,1)为 n 维向量, T 表示向量转置, i 为分量均为1的 n 维列向量。
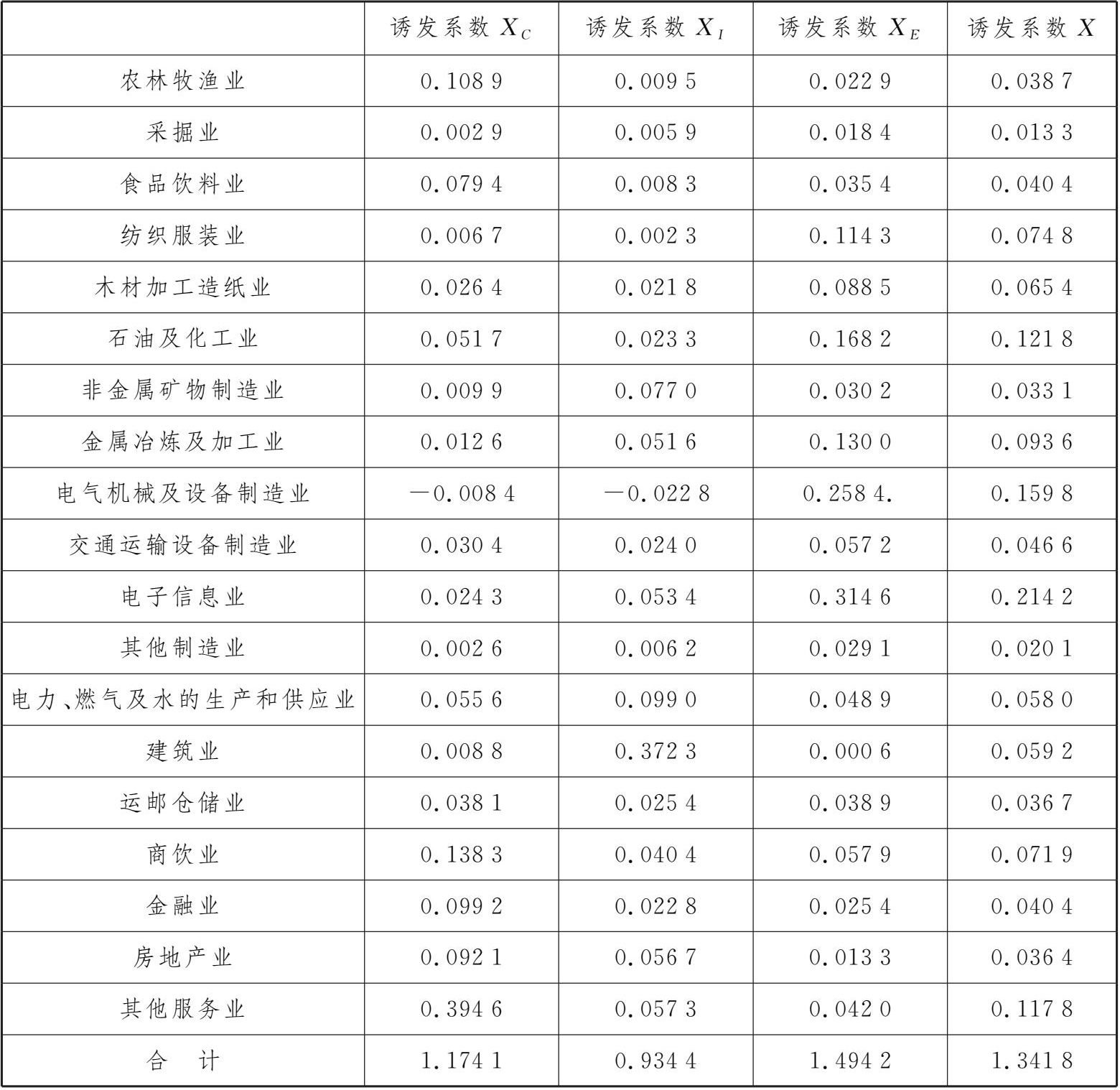
选择20行和4列新区域,输入“=”,选取生产发生诱发额表的所有数据,输入“/”选取最终使用表中的合计行的四个数据,按Ctrl+Shift+Enter键,就可得到生产诱发额系数表。根据定义计算得到该地区2022年生产诱发系数表(见实验表4-1-4)。
实验表4-1-4 某地区2022年生产诱发系数表
(3)生产依存度
利用生产诱发额可对某一产业最终需求的各项目进行最终需求依存度的分析。所谓某产业最终需求各项目的依存度,是指该项目的生产诱发额与该产业所有最终需求项目生产诱发额的合计之比。通过最终需求项目的依存度分析,一些与消费似乎没有关系的产业,通过波及效应,最终竟也有相当的比重是依赖于消费的。当然,通过分析,还可以了解到哪些产业是“消费依赖型”的,哪些产业是“投资依赖型”的,哪些产业是“出口依赖型”的。生产依存度定义如下:
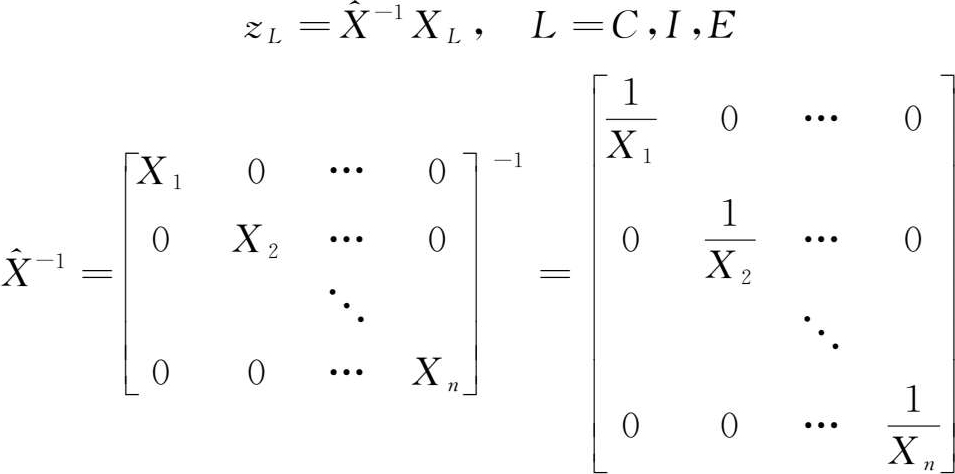
式中, z C , z I , z E 分别表示最终消费、资本形成、出口的生产依存度系数向量。
选择一个19行和19列的新区域,输入“0”,按Ctrl+Shift+Enter键,把对角元素改为诱发额 X 列矩阵的对应数据,得到矩阵 X 。
再选择一个19行和19列的新区域,单击工具栏上的函数工具,选中数学与三角函数中的MINVERSE函数(矩阵求逆函数),选取矩阵
X
,然后按Ctrl+Shift+Enter键,就可以得到矩阵
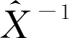 。选择一个19行和4列的新区域,单击工具栏上的函数工具,选中数学与三角函数中的MMULT函数(矩阵相乘函数),选取矩阵
。选择一个19行和4列的新区域,单击工具栏上的函数工具,选中数学与三角函数中的MMULT函数(矩阵相乘函数),选取矩阵
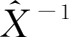 ,再选取生产诱发额表的所有数据,然后按两次Ctrl+Shift+Enter键,就可以得到生产依存度,根据定义进行计算得到该地区2022年最终使用生产依存度表(见实验表4-1-5)。
,再选取生产诱发额表的所有数据,然后按两次Ctrl+Shift+Enter键,就可以得到生产依存度,根据定义进行计算得到该地区2022年最终使用生产依存度表(见实验表4-1-5)。
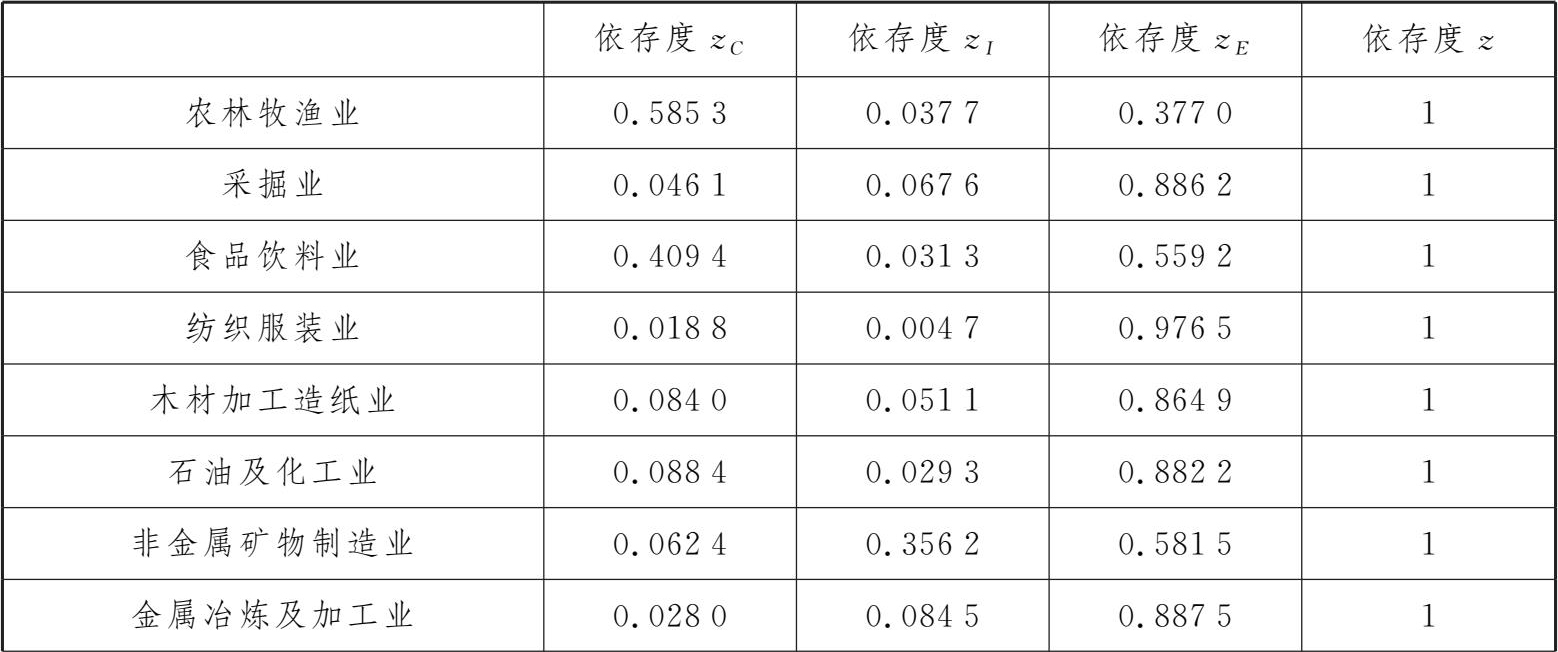
实验表4-1-5 某地区2022年最终使用生产依存度
续表
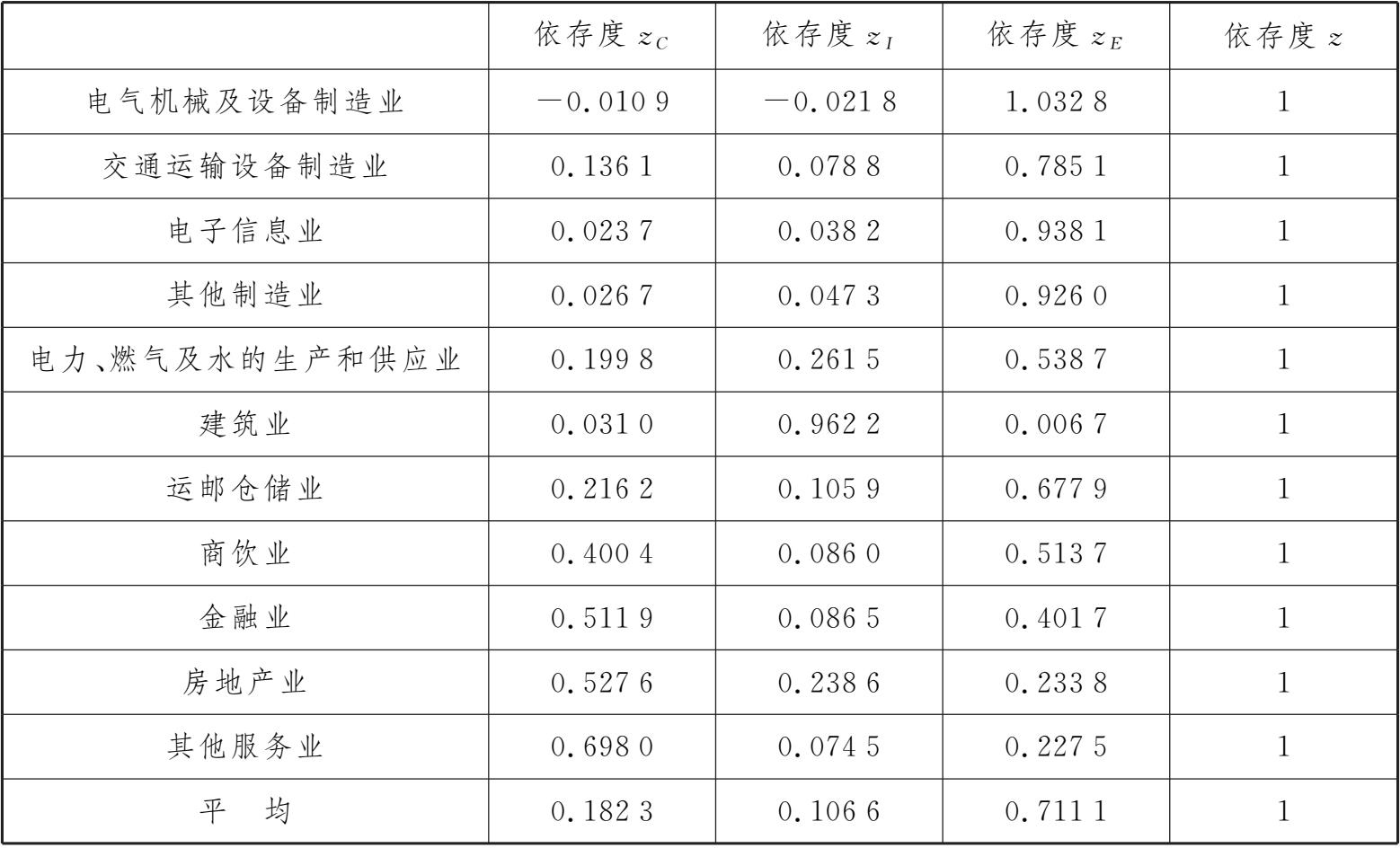
利用生产诱发额可对某产业最终需求的各项目进行最终需求依存度分析:农林牧渔业、食品饮料业、商饮业、其他服务业、金融业、房地产业其最终消费的依存度较高,可将这些产业归属于“消费依赖型”产业;非金属矿物制品业和建筑业其资本形成的依存度较高,可将这些产业归属于“投资依赖型”产业;采掘业,纺织服装业,木材加工造纸业,石油及化工业,金属冶炼及加工业,电气机械及设备制造业,交通运输设备制造业,电子信息业,其他制造业,电力、燃气及水的生产和供应业,运输仓储业其输出的依存度较高,即可将这些产业归属于“出口依赖型”产业。
(4)最终需求结构对增加值影响分析
最终需求结构影响总产出,总产出结构又会影响增加值。利用增加值系数可对各产业的增加值诱发额和增加值诱发系数进行分析。
第一,计算增加值诱发额。
增加值诱发额定义如下:
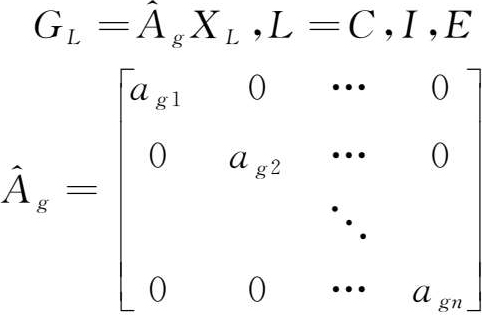
式中, G C , G I , G E 分别表示最终消费 F C 、资本形成 F I 、出口 F E 通过 X C , X I , X E 诱发出的增加值向量。
求对角矩阵
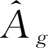 对角元素为增加值与总投入之比。求增加值诱发额矩阵
G
L
,选择一个19行和4列新区域,单击工具栏上的函数工具,选中数学与三角函数中的MMULT函数(矩阵相乘函数),选取矩阵
对角元素为增加值与总投入之比。求增加值诱发额矩阵
G
L
,选择一个19行和4列新区域,单击工具栏上的函数工具,选中数学与三角函数中的MMULT函数(矩阵相乘函数),选取矩阵
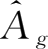 ,再选取诱发额
X
的19行和4列矩阵,然后按两次Ctrl+Shift+Enter键,合计行运用求和可得。根据定义计算得到该地区2022年增加值诱发额表(见实验表4-1-6)。
,再选取诱发额
X
的19行和4列矩阵,然后按两次Ctrl+Shift+Enter键,合计行运用求和可得。根据定义计算得到该地区2022年增加值诱发额表(见实验表4-1-6)。
实验表4-1-6 某地区2022年最终使用生产诱发额表 单位:万元
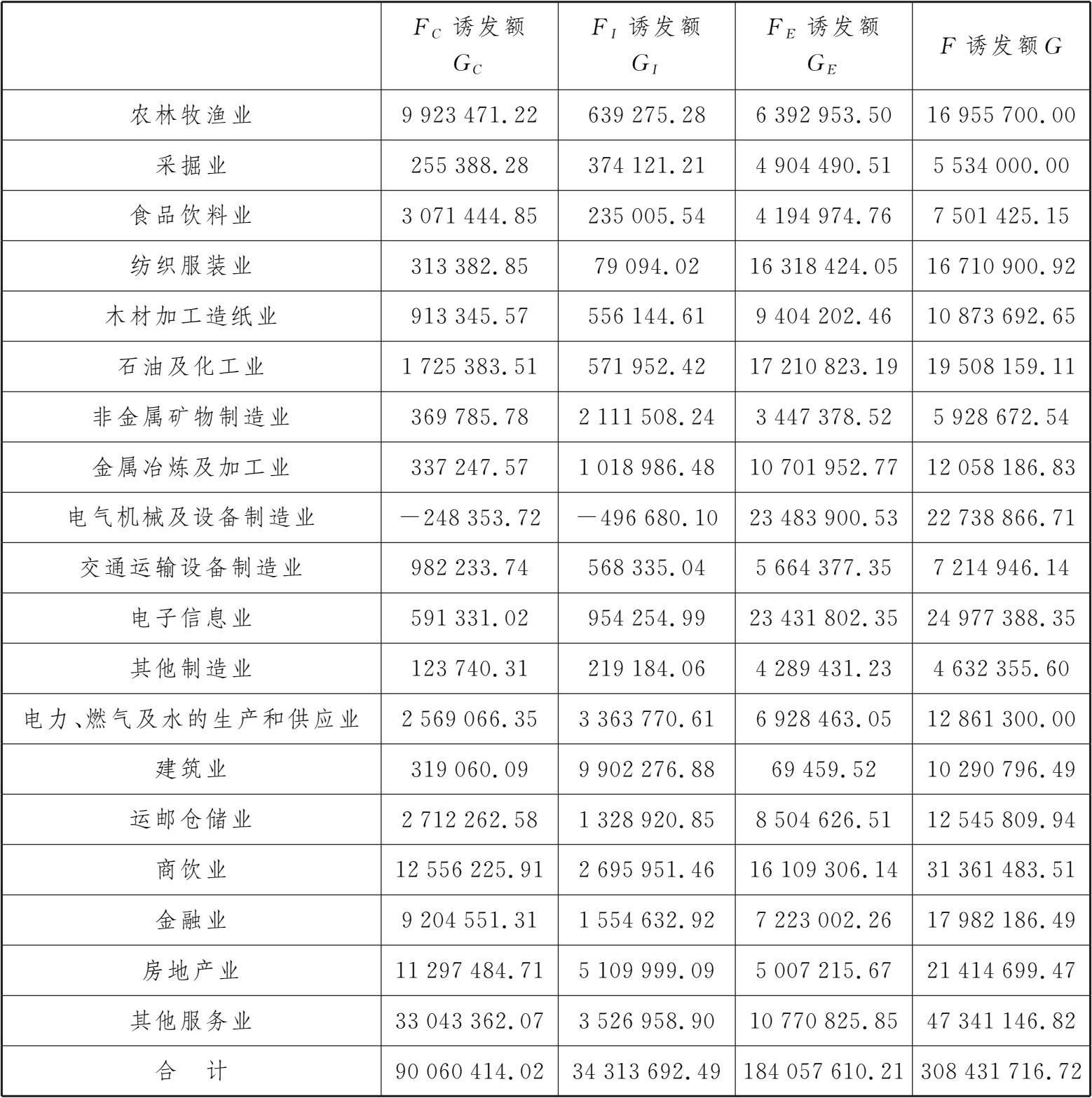
第二,计算增加值诱发系数。
增加值诱发系数是诱发增加值与相应的最终需求额合计之比,其含义是某项最终使用若增加一个单位,则相应的增加值将要增加多少个单位。增加值诱发系数定义如下:
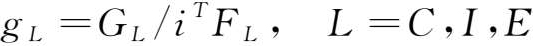
式中, g C , g I , g E 分别表示最终消费、资本形成、出口的增加值诱发系数向量。
选择一个20行和4列的新区域,输入“=”,选取增加值诱发额表的所有数据,输入“/”选取最终使用表中的合计行的四个数据,然后按Ctrl+Shift+Enter键,就可得到增加值诱发额系数表。根据定义计算得到该地2022年增加值诱发系数表(见实验表4-1-7)。
实验表4-1-7 某地区2022年最终使用增加值诱发系数
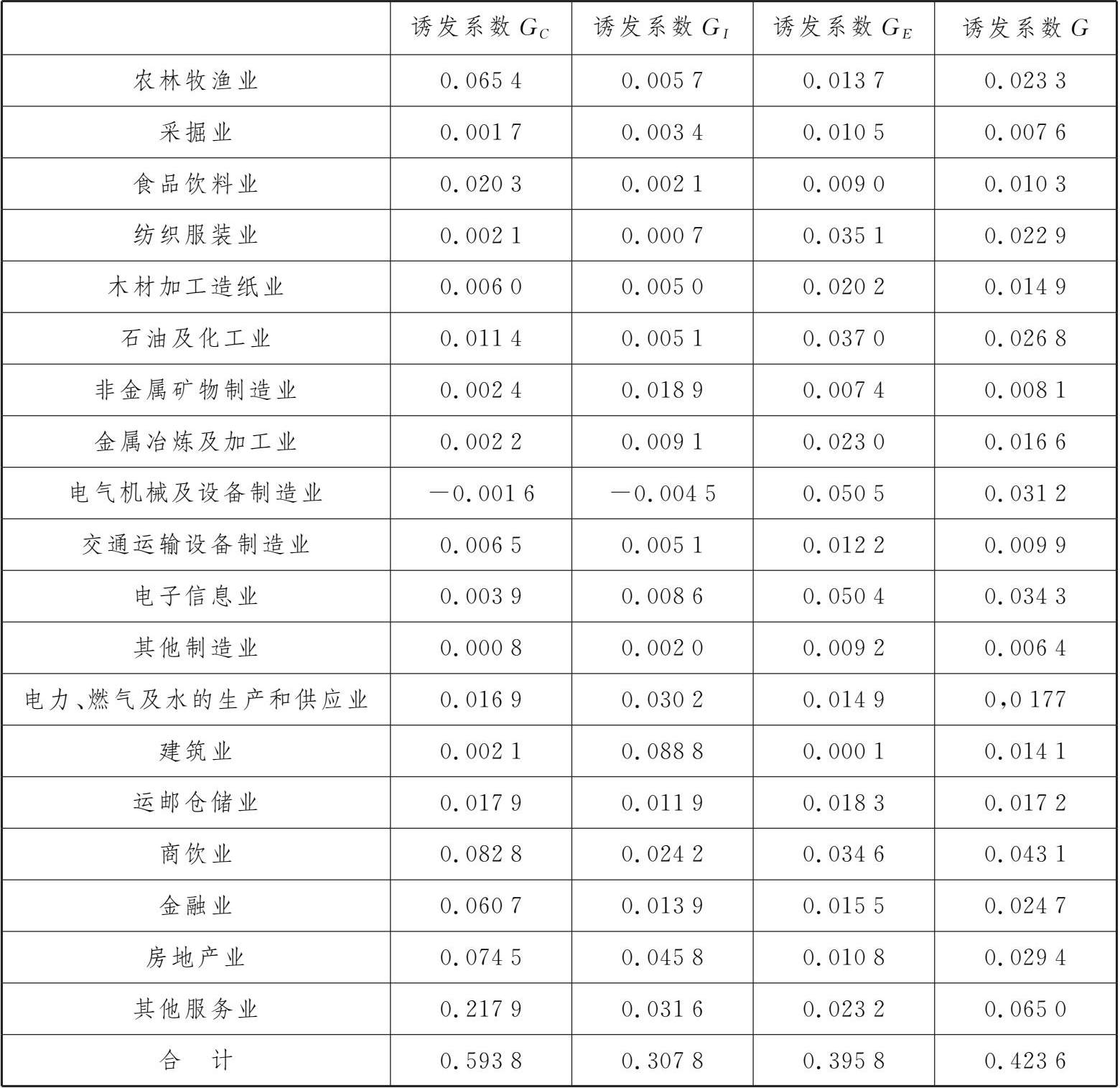
在实验的过程中,由于实践操作,可以更加深入理解各种投入产出系数表里多种数据的关系含义及其数据中比较得出的其他数据模型,从而在其中找到更多有利的数据。由于在处理投入产出表时,实验数据繁多且比较复杂,要有足够的耐心去处理数据,在利用模型得出结果时也要非常小心。因此,为了得出投入产出分析的各种均衡解,不仅要有技术条件做保障,还应该提供生产活动所需的全部必要投入量。同时,通过投入产出分析对输入的不同处理方式说明投入产出分析基本模型的各种类型。
在实验的过程中运用了Excel软件中的很多函数,如求和函数sum、求两组矩阵的乘积的函数mmult、求矩阵的逆的函数minverse等。运用多种方法计算不同的模型,可以节省很多时间。