




在此前关于列昂惕夫逆矩阵与垂直分工的说明中看到,列昂惕夫逆矩阵作为产业链上各产业承担的均衡分工产出模型,反映了各产业在其中承担的全部分工生产情况。不过,我们还有必要进一步了解各分工产业在其中所创造的增加值即增加值收入。换句话说,列昂惕夫逆矩阵虽然刻画了垂直分工,但反映的是产值层面的生产链而不是增加值层面的价值链。
考察价值链,需要进一步考虑各产业是以怎样的增加值率水平
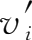 完成上述分工生产从而获得相应的增加值收入的,而这正是增加值基准分工率模型所刻画的内容。
完成上述分工生产从而获得相应的增加值收入的,而这正是增加值基准分工率模型所刻画的内容。
以
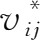 表示
i
产业参与并承担
j
产业单位最终产品的垂直分工生产而获得的增加值收入,则:
表示
i
产业参与并承担
j
产业单位最终产品的垂直分工生产而获得的增加值收入,则:
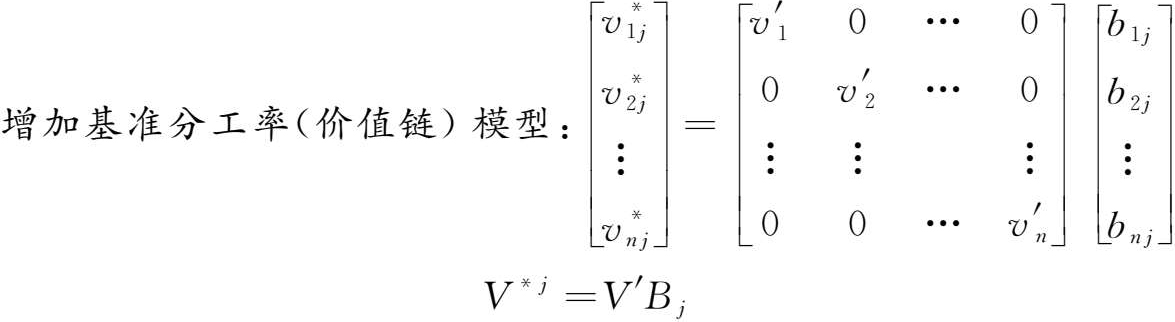
以上就是增加值基准分工率模型,同时也是 j 产业的价值链分工模型。
这里, B j 为列昂惕夫逆矩阵的第 j 列向量。将各 j 最终品的价值链组合成矩阵,则该矩阵为:
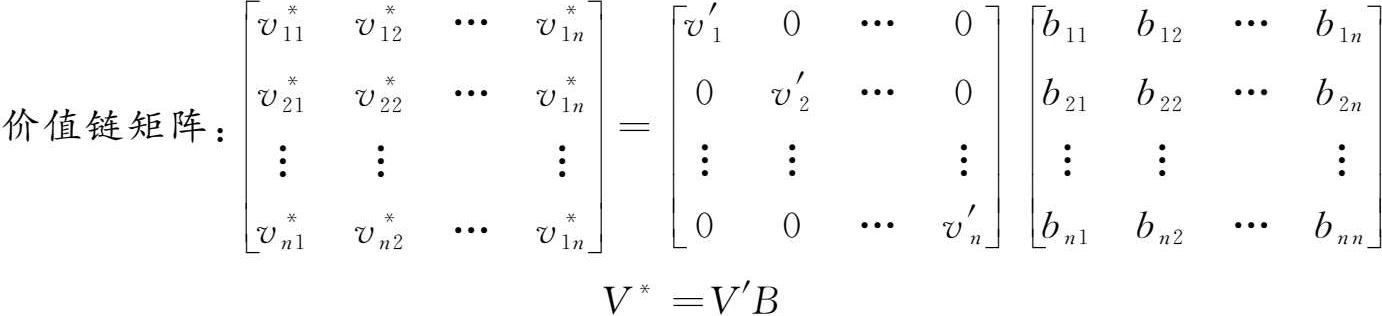
增加值基准分工率即价值链模型的特点是其要素合计在不考虑中间品进口的情况下恰好是1,即
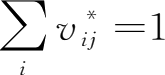 。因此,价值链列向量中的要素
。因此,价值链列向量中的要素
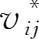 直接表示了
i
产业在
j
最终品价值链中的收入份额。
直接表示了
i
产业在
j
最终品价值链中的收入份额。
单元结构模型试图对列昂惕夫逆矩阵的各列向量从垂直分工体系的角度加以解构。我们已经了解到列昂惕夫逆矩阵 B 的 j 列向量反映的是基于垂直分工的逐级扩展而决定下来的各产业的均衡分工总产出,也由此而知道这一总产出列向量的背后是一个围绕 j 产业最终品的一个垂直分工体系。那么,这一垂直分工体系中的各分工产业之间究竟产生了哪些中间品供求呢?单元结构就是要刻画某一最终产品的垂直分工体系中,参与其中的各产业相互间发生了怎样的中间品供求,从而进一步考察这一垂直分工体系中的结构特征。
我们知道,投入产出表尤其是其中的中间投入—中间需求矩阵以棋盘格状的矩阵布局巧妙地归纳了产业部门之间的中间品供求。下面,我们以投入产出表为框架并以第1产业最终品为例,来说明单元结构模型的模型思路。
首先,我们考虑一个只在第1产业产出1单位最终产品的经济体。由产业链均衡分工产出模型可知,该经济体的各产业均衡总产出就是列昂惕夫逆矩阵的第1列。于是,如图3-2所示,如果用投入产出表框架归纳这样的经济体,则首先,其最终需求矩阵中对第1产业有1单位最终需求;其次,其横向的总需求合计也就是总产出合计,是列昂惕夫逆矩阵的第1列列向量;进而,鉴于体系中的平衡关系,其纵向的总投入合计也就是总产出合计,是对列昂惕夫逆矩阵第1列列向量转置得到的行向量。
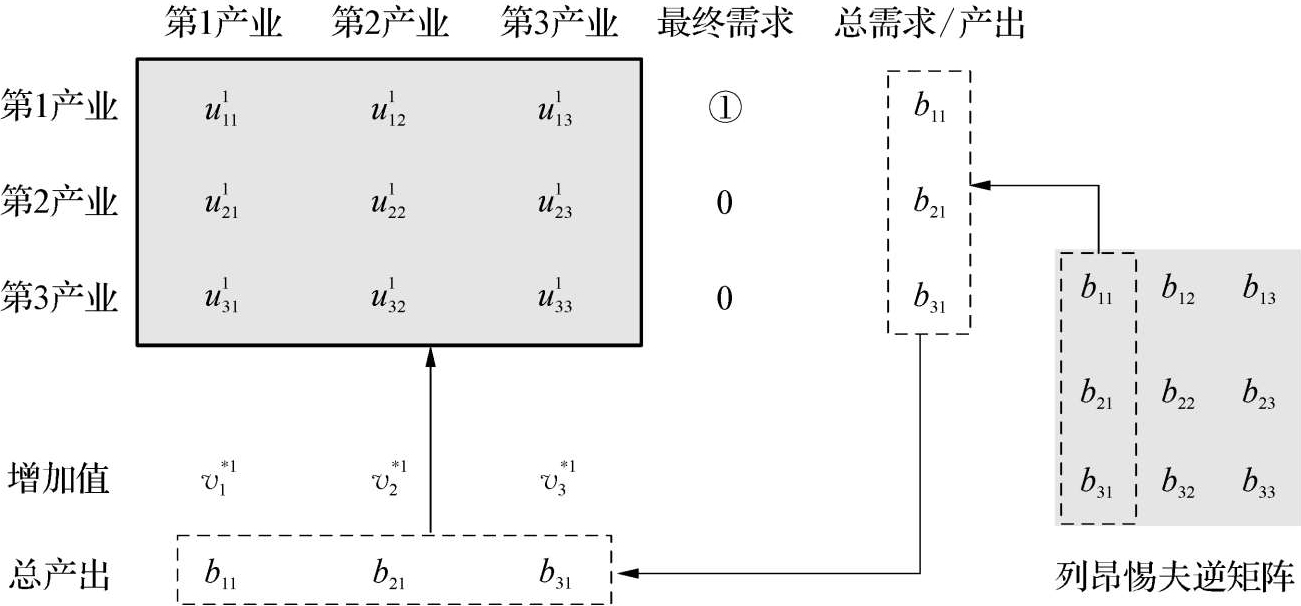
图3-2 第一产业的单元结构 U 1
现在可以看出,这一投入产出表框架中的中间投入、中间需求矩阵就是我们想要获得的单元结构 U 1 ,而这在有了该体系的各产业均衡总产出的基础上可通过下式得到:

将上述公式一般化,对于任意 j 产业1单位最终品,其单元结构 U j 为:
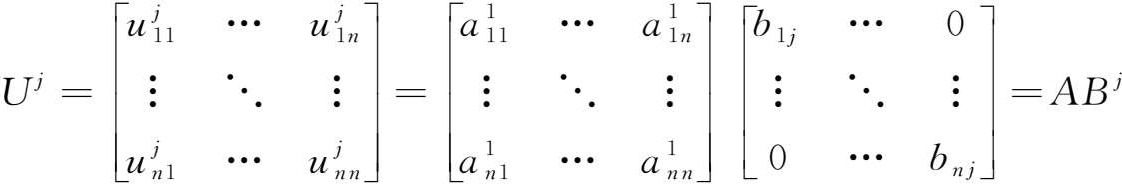
这里, B j 表示以列昂惕夫逆矩阵第 j 列要素为对角要素的对角矩阵。
当注意到图3-2中的增加值行向量可通过下式得到:
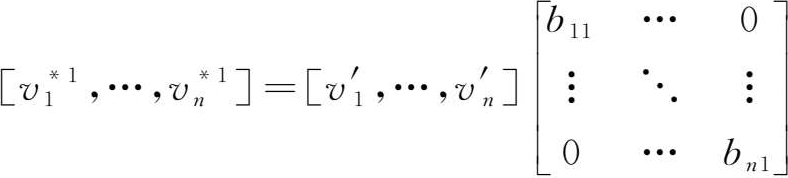
而该式是前述价值链模型的转置:
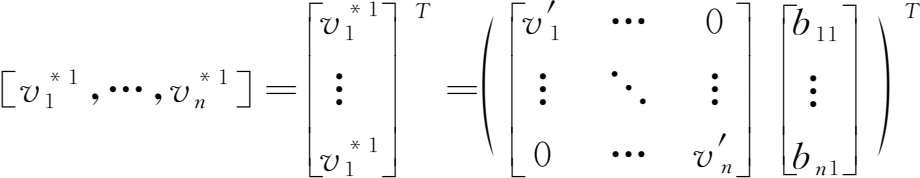
式中, T 表示转置。
可见,上述这一投入产出表框架完整地整合归纳了以第1产业最终品的产出作为一个垂直分工体系单元,其中的生产链、价值链以及单元结构等各方面内容及其相互关系,具体如图3-3所示。
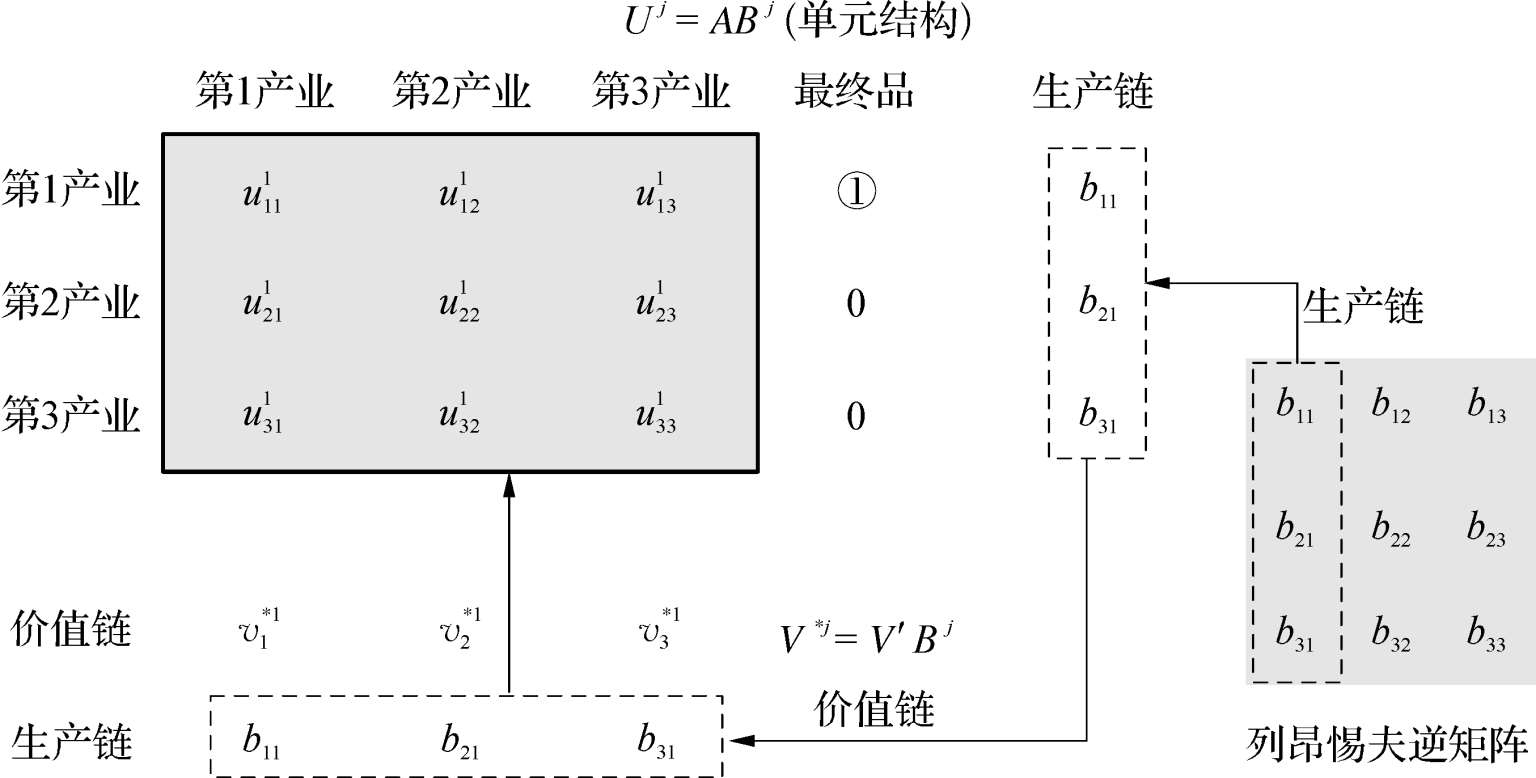
图3-3 第1产业的单元垂直分工体系
在这一投入产出表范式的单元垂直分工体系中,有相应的平衡关系。
首先,单元结构 U j 中各要素的横向合计加之最终品产出等于该单元的生产链上的各产业总产出,也就是列昂惕夫逆矩阵第 j 列向量中的各要素,即:
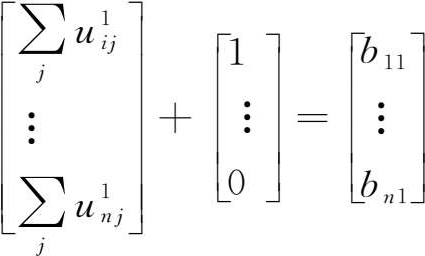
其次,价值链上各产业的增加值合计等于当前的1单位最终需求,即:
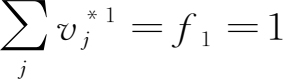
最后,我们可参照以上第1产业最终品的单元垂直分工体系,相应构建任一 j 产业最终品的单元垂直分工体系。
由均衡产出函数可知,给定最终需求向量 F ,则各产业的均衡总产出为:
X = BF
可在此基础上通过引入各产业的增加值系数得到各产业的收入(增加值)函数,即产业收入(增加值)函数:
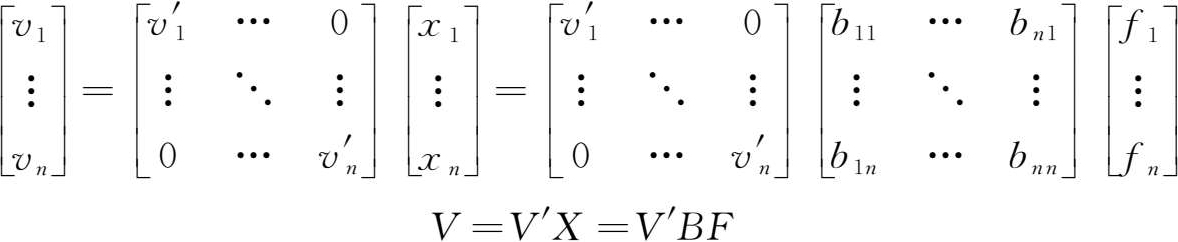
进一步地,可在上述产业收入(增加值)函数基础上构建各产业增加值在增加值总量中的份额构成,也就是生产法国民生产总值中各产业增加值的份额构成,即产业结构函数:
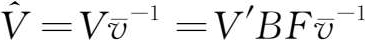
这里,
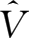 是由各产业增加值在增加值总额中的份额
是由各产业增加值在增加值总额中的份额
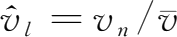 构成的列向量,
构成的列向量,

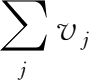 ,即各产业增加值合计。考虑到在没有进口的情况下收入法GNP合计=生产法GNP=支出法GNP合计,即
,即各产业增加值合计。考虑到在没有进口的情况下收入法GNP合计=生产法GNP=支出法GNP合计,即
 。这里,
。这里,
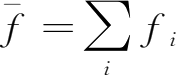 。则上式可变换为:
。则上式可变换为:
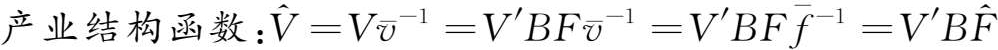
这里,
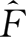 是由最终需求中的各产业份额
是由最终需求中的各产业份额
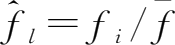 构成的列向量。
构成的列向量。
我们不难从产业分工的视角理解上述产业结构函数。首先,从产业分工的角度来看,最终需求中的各产业份额户反映的是水平分工。其次,我们此前基于价值链模型得到了价值链矩阵:
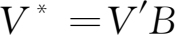
将其代入产业收入函数及产业结构函数:

可以看出,产业收入函数及产业结构函数将产业收入和产业结构呈现为水平分工与垂直分工结合。也就是说,收入法国民生产总值中的各产业增加值以及此意义上的产业结构,是水平分工与垂直分工的复合结果。这样,对于其中的任一产业,有:
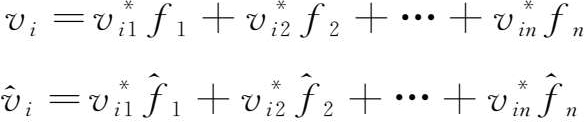
首先,可以看出,
i
产业增加值收入
v
i
是
i
产业在各最终品价值链中的收入份额
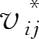 与各最终品的需求量
f
j
的乘积和:
与各最终品的需求量
f
j
的乘积和:
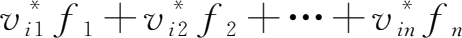 。在此,价值链
V
*中的要素
。在此,价值链
V
*中的要素
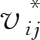 起到分配系数的作用,将满足最终需求所实现的最终产品的价值
f
j
按
i
产业在其价值链中的份额
起到分配系数的作用,将满足最终需求所实现的最终产品的价值
f
j
按
i
产业在其价值链中的份额
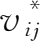 分配至
i
产业
分配至
i
产业
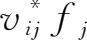 。
。
其次,可以看出,与之相似,
i
产业增加值在全部增加值中的份额
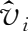 是
i
产业在各最终品价值链中的收入份额
是
i
产业在各最终品价值链中的收入份额
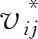 与各最终品在需求量中的份额
与各最终品在需求量中的份额
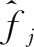 的乘积和:
的乘积和:
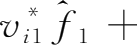
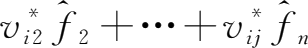 。在此,各最终品在需求量中的份额
。在此,各最终品在需求量中的份额
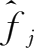 起到了权重系数的作用,将各产业在各最终品价值链中的份额
起到了权重系数的作用,将各产业在各最终品价值链中的份额
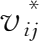 按最终品在需求量中的份额
按最终品在需求量中的份额
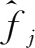 进行了加权平均。
进行了加权平均。
上述公式也常被解读为给定的最终需求通过 V *而诱发形成的各产业增加值,故而 V *又被称为最终的增加值诱发系数。
需要留意的是,如前所述,在不考虑进口的情况下 V *各列向量的要素合计为1,因此,该系数作为增加值诱发效果的系数,与其作为价值链的收入份额系数一样,主要在结构层面上有分析意义。