




投入产出分析最基本的问题是,通过公式 X =( I - A ) -1 F ,在假定生产技术不发生变化的时期内,根据给出的与基期不同的最终需求,得到各部门的均衡产出量。所谓均衡产出量,就是既能满足最终需求,又能满足中间需求的各产品部门产出量,既无剩余,也不足。
我们把公式中的( I - A ) -1 矩阵称为列昂惕夫逆矩阵,列成表格称列昂惕夫逆系数表,是广义投入产出表的第三个表(见表3-3)。
表3-3 列昂惕夫逆系数表

为方便说明列昂惕夫逆系数的经济含义,我们假定只有两个产品部门,第1产品部门的最终需求为1个单位,第2产品部门的最终需求为0,根据公式 X =( I - A ) -1 F ,有:
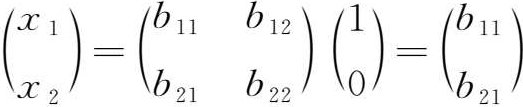
该计算说明,列昂惕夫逆矩阵第1列第1个元素 b 11 表示为得到1个单位第1产品部门的最终产品所需的第1产品部门的产出量,第1列第2个元素 b 21 表示为同一目的所需的第2产品部门的产出量。因此,列昂惕夫逆矩阵第1列各元素表示为得到第1产品部门1个单位的最终产品而需要各产品部门提供的产出量,其中第1个元素,即第1产品部门提供的产出量,除了满足本部门直接生产过程的消耗需求及派生出来的消耗需求外,还要满足1个单位的最终产品需求(因此推论 b 11 一定大于或等于1);第2产品部门虽不需要提供最终产品,但为满足第1产品部门直接生产过程的消耗需求及派生出来的消耗需求,就必须生产 b 21 单位的总产出量。
上述结论很容易推广到一般,列昂惕夫逆矩阵第 j 列元素表示,当 j 产品的最终需求增加1个单位时,对各产品部门所产生的直接和间接的影响:第 j 产品部门的产出量(列昂惕夫逆矩阵主对角线上的元素)除满足由此带来的全部生产过程的直接和间接的消耗需求外,还要满足1个单位的最终产品需求量,因而大于或等于1;其他部门的产出量 b ij ( i ≠ j )都是用来满足由此带来的全部生产过程中的直接和间接的消耗需求。
我们按照均衡产出函数来逐步展开均衡产出解的产生过程,以此来理解最终需求的生产波及效果与列昂惕夫逆矩阵的含义。当给出最终需求量向量 F 时,由均衡产出函数 X = AX + F 可知,这将最直接地要求有等量的产出量 X 1 与之适应,即 X 1 = F ,或:
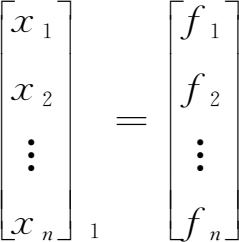
接下来,基于均衡产出函数中内生于总产出 X 的中间需求函数 AX 可知, X 1 的产出量将形成 AX 1 = AF 的中间需求量,并将要求相应的产出量与之适应,即 X 2 = AX 1 = AF ,或:

而 X 2 的产出量将进一步地形成 AX 2 = AAX 1 = AAF = A 2 F 的中间需求变量,以及要求相应的产出量 X 3 = AX 2 = AAX 1 = AAF = A 2 F ,即:

这一过程将重复下去,继续产生 X 4 = AX 3 = AAAX 1 = AAAF = A 3 F 的中间需求。于是,与所有这些需求总和相适应的均衡产出量应为:
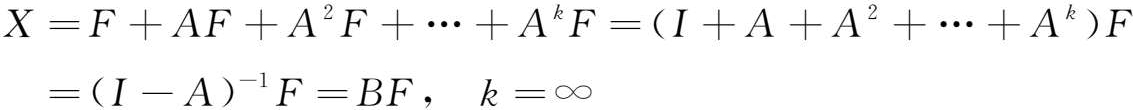
或者表示为:
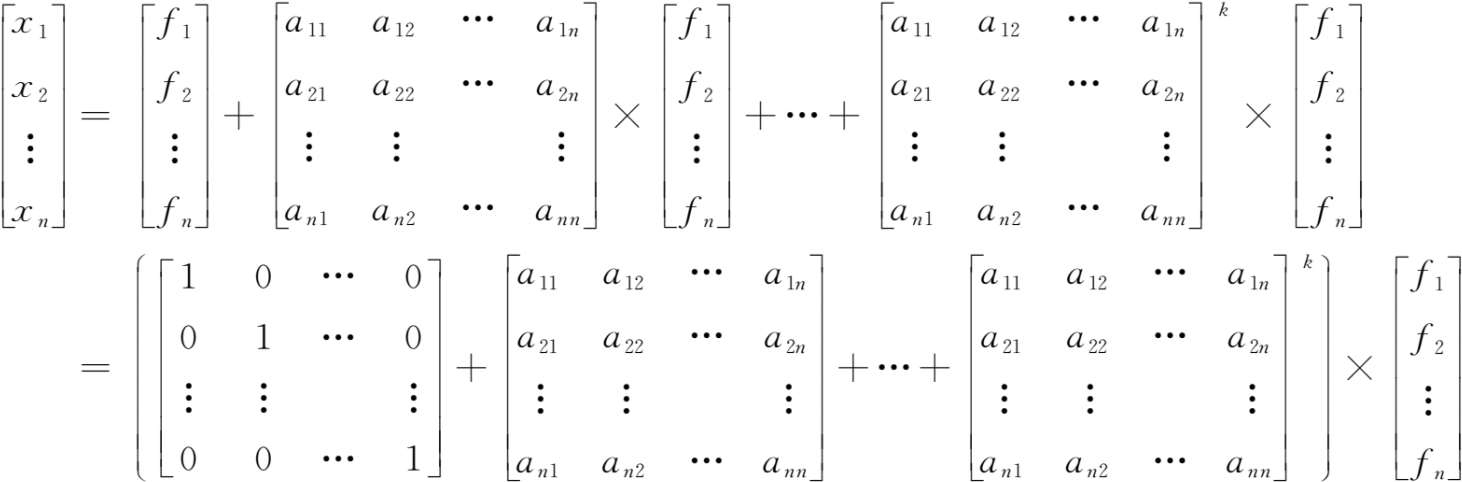
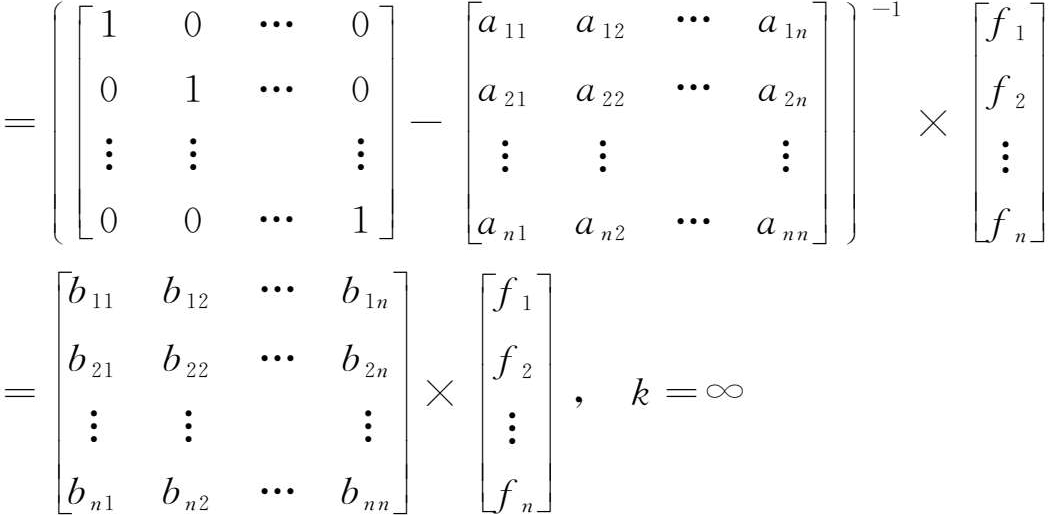
由此可以看出:
第一,最终需求的生产波及效果。
在均衡产出函数 X = AX + F 之下,通过其中内生于总产出的中间需求函数 AX ,最终需求 F 将以最终品的生产活动为发端,沿着 AF , A 2 F ,…, A k F 逐级引致派生出一系列的中间品的供求关系,使得满足该最终需求所需的生产活动扩展波及最终品以外的其他产业部门。我们称此为最终需求的生产波及效果。
第二,最终需求的产出乘数效果。
鉴于最终需求及其生产波及效果,除非中间投入全部为0的特殊情况,否则,由此决定的均衡产出量将大于最终需求量,即( I + A + A 2 +…+ A k ) F > F 。我们将这种最终需求量对于均衡产出量的倍数放大效果称为乘数效果。
生产波及效果与乘数效果显然是两位一体的。前者突出强调了最终需求在均衡产出函数下将会对其所要求的均衡产出从最终品产业渐次地扩展波及相关中间品产业;后者则突出强调了最终需求在均衡产出函数下将会基于生产波及效果而要求其自身倍数以上的均衡总产出量。
如前所述,生产波及效果与产出乘数效果是两位一体的,正是基于最终需求的生产波及效果因而会对产出形成其自身倍数以上的均衡总产出量的产出乘数效果。以下以第1产业的1单位最终需求为例,归纳了其生产波及效果的各层级及其与产出乘数效果的关系:
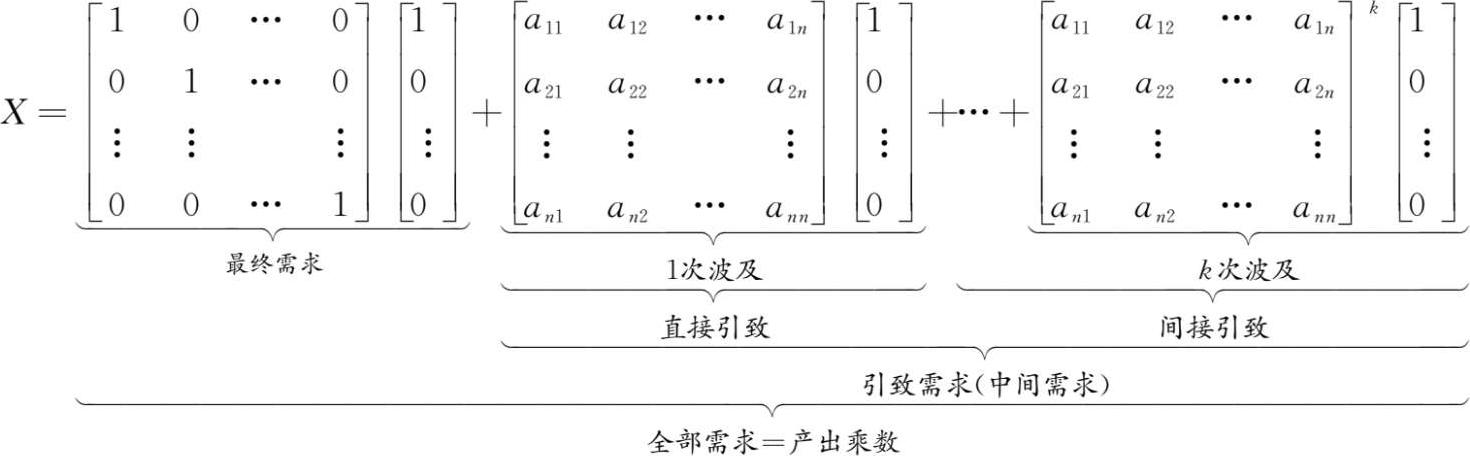
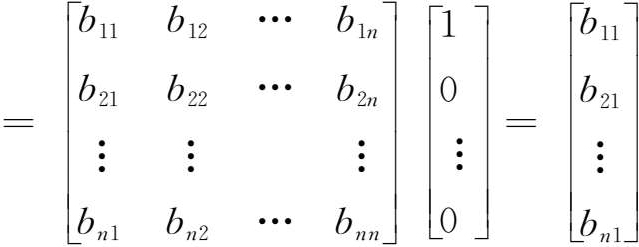
在此,我们把最终需求基于生产波及效果而引致的中间需求称为引致需求。进一步地,从引致需求是基于生产波及效果而渐次产生的角度上,我们把其中由最终需求所最直接引致的中间需求 AF 即“直接原材料”称为“直接引致”,也称1次波及;把由此而进一步引致的中间需求 AF ,…, A k F 即“原材料的原材料”统一称为“间接引致”,或依次称为2次波及、3次波及、 k 次波及。
从数量层面来看,最终需求在其生产波及效果的各层级即1次波及…… k 次波及上所形成的引致需求量分别为 AF , A 2 F ,…, A k F ,其全部的引致需求总量则为:
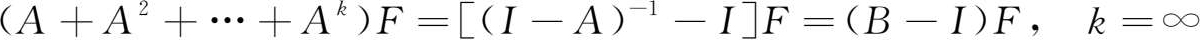
而由最终需求量和引致需求量构成的需求总量及其所要求的均衡总产出量则为:
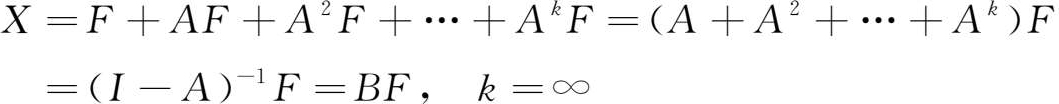
首先,可以看出, A ,…, A n 是最终需求量与其各级波及效果上的引致需求量之间的比例系数。为此,我们把 A 称为直接引致系数矩阵或1次波及系数矩阵,把 A 2 ,…, A n 依次称为 k 次引致系数矩阵或 k 次波及系数矩阵。
其次,可以看出, B - I 是最终需求量与其全部的引致需求量之间的比例系数。为此,我们把 B - I 称为全部引致系数矩阵或完全波及系数矩阵。
再次,可以看出,列昂惕夫逆矩阵 B 是最终需求量与其基于生产波及效果而倍数放大的需求总量进而均衡产出量之间的比例系数。为此,我们把列昂惕夫逆矩阵 B 称为产出乘数矩阵。
最后,从上述示例可以看出,对于具体的 j 产业的单位最终需求而言,其生产波及效果以及与之等义的产出乘数效果体现在上述矩阵中的 j 列向量上。以列昂惕夫逆矩阵为例,其第 j 列向量上的第 i 要素表示 j 产业的单位最终需求对于 i 产业的生产波及效果的合计,同时也是对其产出乘数效果的合计。
如前所述,在涵盖中间投入的列昂惕夫型生产函数中,产品的生产是基于垂直分工的加工生产。下面,我们以第1产业生产1单位最终产品为例,考察其中的分工生产活动。
首先,根据列昂惕夫生产函数,第1产业生产1单位最终品需要其垂直分工链条上的上游
i
产业为其提供中间品
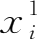 ,即:
,即:

其次,由于各中间品产业也是基于垂直分工的加工生产,也需要其垂直分工链条上的上游产业为其提供中间品,即:

后面,这一过程将重复下去:

于是,与所有这些基于垂直分工而发生在上游的中间投入总量同时也是其要求的各产业为此提供的中间品总量为:

最后,包括第1产业的单位最终品产出在内,其生产链上各产业的全部产出即为产业链均衡分工产出,函数为:

显然,这一结果正是列昂惕夫逆矩阵的第1列,均衡分工产出(产业链)模型: X j = BF i=j=1 = B j
这里, X j 表示1单位 j 最终产品所需各产业的均衡分工产出列向量, F i=j=1 表示第 i = j 要素为1、其他要素为0的列向量, B j 为列昂惕夫逆矩阵的第 j 列向量。也就是说,从垂直分工的角度来看,列昂惕夫逆矩阵的各列向量反映的是各个产业的垂直分工链条上的均衡分工总产出。
首先,可以看出,最终需求的生产波及效果和乘数效果与这里的最终产品的垂直分工(产业链)的分工产出是等义的。最终需求之所以会派生出引致的中间需求,就是因为最终产品的生产是基于垂直分工的生产,需要参与垂直分工的各产业提供中间品,从而产生生产波及效果,同时也产出乘数效果。
其次,可以看出,垂直分工是一个逐级扩展且相互联系的分工体系,而此前对生产波及效果的层级解构同样适用于对垂直分工体系的层级解构。我们据其分工层级 A ,…, A k 将其分为1级垂直分工乃至 k 级垂直分工,将1级垂直分工中即其直接上游的中间品投入称为直接投入,将此后各级垂直分工即上游的上游的中间品投入称为间接投入。
另外,在数量层面上,我们把1级垂直分工的 A 称为直接投入系数矩阵,把 A 2 ,…, A k 依次称为 k 级垂直分工下的间接投入系数矩阵, B - I 称为全部投入系数矩阵,也被称为完全消耗系数矩阵;把列昂惕夫逆矩阵 B 称为生产链均衡产出矩阵。
最后,与生产波及效果和产出乘数效果同样,对于具体的 j 产业最终品而言,其垂直分工链条上的各产业的分工生产活动具体体现在上述各系数矩阵的 j 列向量上。以列昂惕夫逆矩阵为例,其第 j 列向量上的第 i 要素表示 i 产业在 j 产业的单位最终品生产中所承担的直接乃至间接的全部的垂直分工产出量。
通过以上说明不难看出,尽管列昂惕夫逆矩阵 B 由中间投入系数矩阵 A 计算而得,并且都反映垂直分工,但双方的视野范围有本质的区别。从波及效果的角度来说,前者( A )仅为直接引致,后者( B )则是直接引致和间接引致的总和;从垂直分工的角度来说,前者仅为直接投入所涉及的上游中间品的分工生产,后者则是直接投入乃至间接投入所涉及的全部中间品生产的总和。
以图3-1所示的汽车生产为例,投入系数的视野范围仅涉及汽车生产中所直接使用到的钢铁部件的投入,而列昂惕夫逆矩阵则进一步涉及为汽车所提供钢铁部件的生产中所使用到的铁矿石的投入。

图3-1 汽车生产的直接投入和间接投入
列昂惕夫逆矩阵是一个正方矩阵,可从横向和纵向两个角度解读。如前所述,投入产出表在纵向上表示投入和产出,横向上表示产出和需求。列昂惕夫逆矩阵同样如此,其纵向上表示某产业的1单位最终品生产所需的直接乃至间接的全部投入,横向上表示某产业所满足的各产业1单位最终品生产所需的全部需求。
按照生产波及效果和乘数效果以及产业链均衡总产出的含义解读该矩阵中各要素数值,利于对其从纵向上按列读取。即择取其中任一列步,则该列向量中的要素含义是:该列所属 j 产业产出 i 单位最终品,此时基于垂直分工而直接乃至间接要求的产业的全部产出量。
表3-4是基于中国2002年投入产出表计算得到的列昂惕夫逆矩阵。可以看出列昂惕夫逆矩阵在数量层面的若干特征。
表3-4 基于中国2002年投入产出表计算得到的列昂惕夫逆矩阵
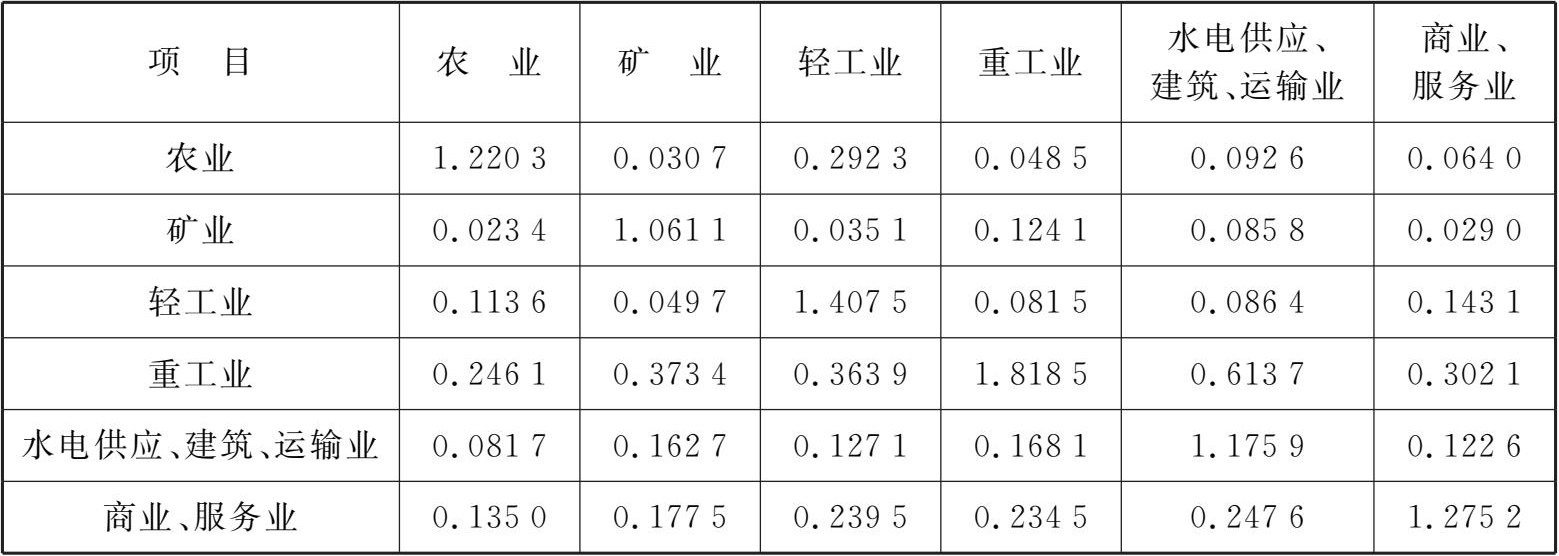
第一,列昂惕夫逆矩阵中的对角要素往往大于1,按照上述解读方式来讲,对角要素是 j 产业产出1单位最终品时对本产业自身所要求的总产出量。由于这一总产出量中除了本产业的1单位最终品产出以外,还包括经由生产波及效果而间接要求的本产业中间品的产出,也就是包括生产波及过程中对本产业的反馈,因而本产业的均衡总产出往往大于1,多出的部分就是反馈波及本产业而形成的中间品产出。
第二,列昂惕夫逆矩阵中纵向各列要素的合计往往大于1,参照上述解读方式来说,列向要素是其所属 j 产业产出1单位最终产品时直接地乃至间接地经由生产波及效果而要求的各个产业 i 的总产出量。或者说包括该最终产品的产出以及纵向产业链上的全部产出。除非该产业的生产活动完全不需要中间投入,也就是说完全没有纵向分工,否则一定会对相关的中间品产业产生大于0的生产波及效果,则对各产业总产出合计往往大于1。