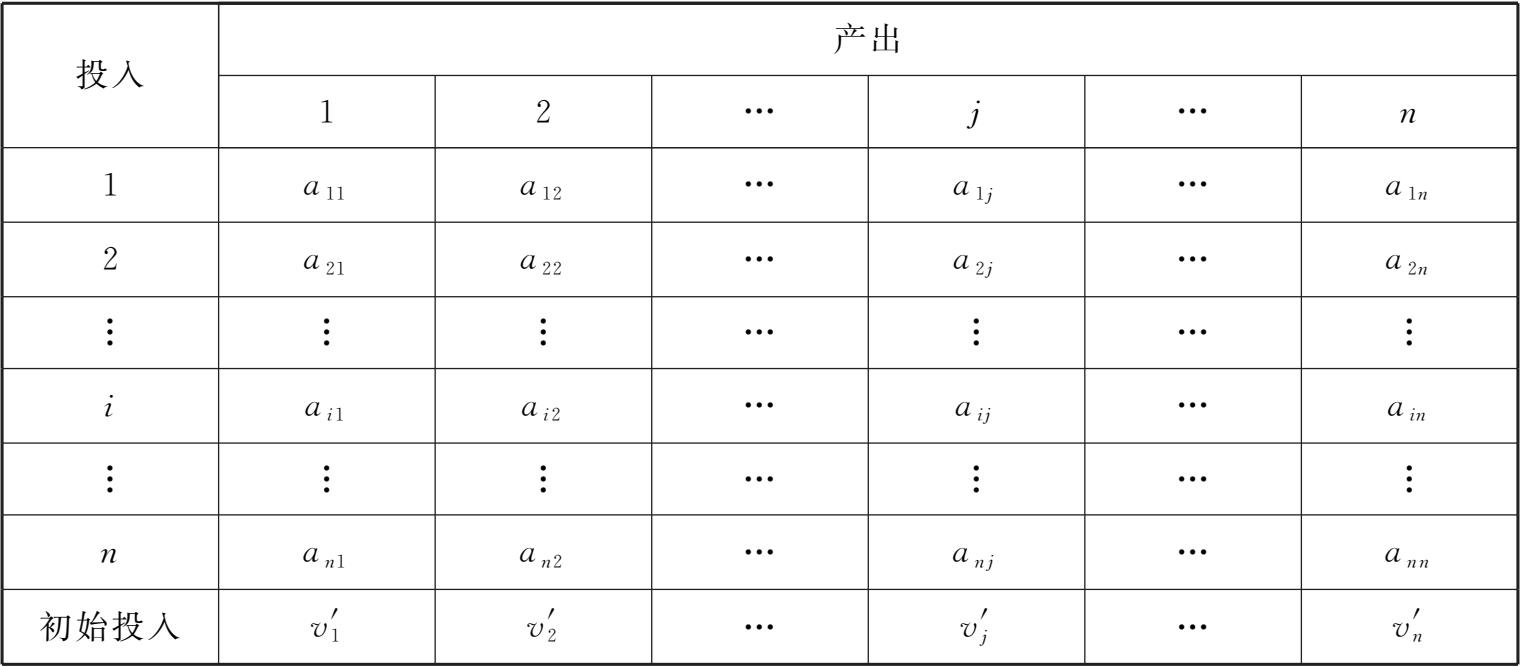
价值型投入产出表的基本平衡关系式如下:
(1)行向平衡关系=中间使用+最终使用=总产出。数学公式为:
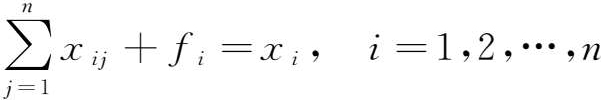
行向平衡关系反映的是各产品部门的供求平衡关系。
(2)列向平衡关系=中间投入+最终投入=总投入。数学公式为:
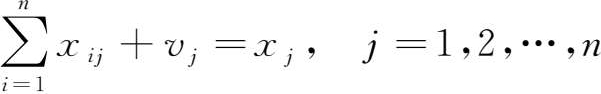
列向平衡关系反映的是各产品部门的收支平衡关系。
上述
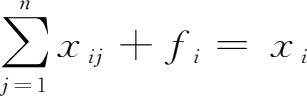 ,
i
=1,2,…,
n
,是用方程式来描述表3-1中各产品部门产出量的供需平衡关系。如果我们根据表3-1所示的特定时点的投入产出关系,利用模型式
,
i
=1,2,…,
n
,是用方程式来描述表3-1中各产品部门产出量的供需平衡关系。如果我们根据表3-1所示的特定时点的投入产出关系,利用模型式
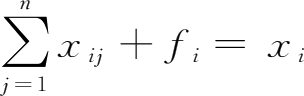 ,
i
=1,2,…,
n
来确定任意时点上产品部门间数量依存关系时,我们必须在模型内部确定各产品部门的产出量
,
i
=1,2,…,
n
来确定任意时点上产品部门间数量依存关系时,我们必须在模型内部确定各产品部门的产出量
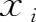 和产品部门之间的流量—中间产品需求量
d
ij
,在模型外部给出分产品部门的最终需求,即最终需求向量(
f
1
,
f
2
,…,
f
n
)。
和产品部门之间的流量—中间产品需求量
d
ij
,在模型外部给出分产品部门的最终需求,即最终需求向量(
f
1
,
f
2
,…,
f
n
)。
一旦确定最终需求向量
F
,就决定了各产品部门的产出量:不仅要满足最终需求
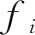 ,还要满足各产品部门生产所产生的派生需求
,还要满足各产品部门生产所产生的派生需求
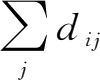 。就是说,各产品部门生产能够满足整个经济总需求的产出量
x
i
,使任何产品部门的产出量都不会过剩也不会不足。这就是式
。就是说,各产品部门生产能够满足整个经济总需求的产出量
x
i
,使任何产品部门的产出量都不会过剩也不会不足。这就是式
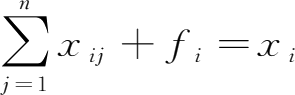 ,
i
=1,2,…,
n
的意义。
,
i
=1,2,…,
n
的意义。
在投入产出表3-1中,中间产品流量 d ij 是 j 产品部门生产 x j 单位时所投入的 i 产品部门的产品量,这只是反映一个具体的生产技术结构,我们无法在表中直接找到,当 j 产品部门的生产量改变后所需要投入的各产品部门的产品量。现在我们大胆假定 d ij 和 x j 之间存在齐次线性关系,因此定义了中间产品的投入系数(也称直接消耗系数)。
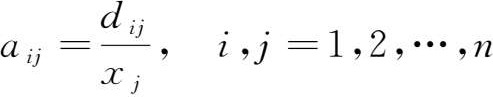
式中, a ij 表示 j 产品部门生产单位总产品所投入的(消耗) i 产品部门产品量。类似地,我们可以定义生产要素(初始投入)的投入系数:
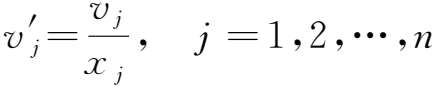
式中,
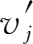 表示产品部门生产单位总产品所投入的生产要素量(用价值量间接地反映)。进一步,我们可以得到价值表的投入系数有下面的关系成立:
表示产品部门生产单位总产品所投入的生产要素量(用价值量间接地反映)。进一步,我们可以得到价值表的投入系数有下面的关系成立:
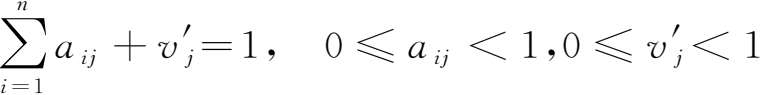
从投入系数的定义可以清楚地看到上述关系的经济意义,因为任何一个产品部门,在生产过程中每一种投入品的价值均不能超过其产出的价值,因此所有中间投入品的价值都不能超过或等于其产出的价值。
实物表也可以同样计算投入系数,但不完全具备上述关系。一般来说,实物表的投入系数非负,不一定小于1,因为各产品的计量单位不同,投入系数大于1是经常有的,但主对角元素——本部门产品的投入系数却一定小于1,因为在生产中对本部门产品的消耗一定不能大于或等于其产出。
由此我们可以得到投入系数表(见表3-2),它体现了投入产出模型中生产结构的基本特征,是广义的投入产出表(投入产出表、投入系数表和后面将要说明的投入产出逆系数表)的三个组成部分之一。
表3-2 投入系数表