




在前几节中,我们所讨论的随机变量都是假设分布已知的。在此前提下,我们研究了随机变量的性质和统计规律,并利用它的数字特征来刻画这种规律。而实际工作中,随机变量的分布往往是部分或完全未知的,我们还没有说明如何确定各种具体的随机现象或随机变量的概率分布形式或数字特征的数值。一般来说,一个具体随机现象的概率特征是很难从物理分析中得到的,必须依靠实验或观测。如何通过对观测资料的分析,对其内在的统计规律作出一定精确程度的判断和预测,这些都属于数理统计的研究内容。
虽然数理统计和概率论一样都是研究随机现象的统计规律以及各种数字特征的,但是它们应用的方法不尽相同。更确切地说,数理统计是从实际观测资料出发来研究随机变量的概率分布与数字特征的,而实际的观测资料总是有限的。在数理统计中,常把研究对象的全体称为 总体 (population)或 母体 ,组成总体的每一个单元称为 个体 (individuality),总体中一部分个体组成的集合称为 样本 或 子样 (sample),样本内所含个体的个数称为 样本容量 (sample size)。
在实际应用中,我们感兴趣的常常是研究对象的一个(或几个)指标,如太阳的相对黑子数、某一波段的射电流量等,它们通常是随机变量。总体通常是指研究对象的某个指标的全部可能值,通常很难得到。因此我们只能根据有限的个体对总体作出判断,这就要求这些个体能够很好地反映总体的情况。在统计理论中,由于各种统计方法都是以独立随机变量的各种性质为基础的,因此要求样本的各个个体应该是 相互独立 的。为了达到这一要求,可以采用简单随机抽样方法,即总体中每一个体被抽到的机会是均等的,并且抽取一个个体不影响总体的成分。事实上,简单随机抽样就是重复独立试验,用简单随机抽样方法获得的样本称为 简单随机样本 (simple random sample)。以后如无特别说明,书中所说的样本都是指简单随机样本。
如果表征总体的随机变量用 X 表示,第 i 次随机试验的结果记为 x i ,则简单随机抽样的结果 x 1 , x 2 ,…, x n 称为总体 X 的一组样本观测值。由于抽样的随机性和独立性,每个 x i 都可看作某个随机变量 X i 所取的观测值。因此, x 1 , x 2 ,…, x n 可以看作 n 维随机变量 X 1 , X 2 ,…, X n 的观测值,而 X 1 , X 2 ,…, X n 为 X 的一个样本,它们相互独立并且与总体具有相同的分布。
当我们考察一个样本时,首先需对其有一个概貌性的了解,以便从中提炼出能反映总体特征的信息。设 x 1 , x 2 ,…, x n 为来自总体 X 的一组样本观测值,对此我们首先计算可以描述其基本特征的特征数。为了与总体的数字特征区别开来,这些特征数常冠以样本两字,即样本数字特征,如:
样本均值 (sample mean)

样本方差 (sample variance)

s 被称为 样本均方差 (sample standard deviation)。
样本 k 阶矩 (sample moment of order k )
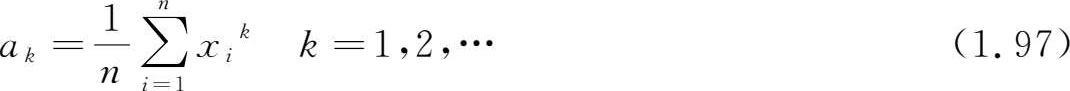
样本 k 阶中心矩 (sample moment of order k about the origin)
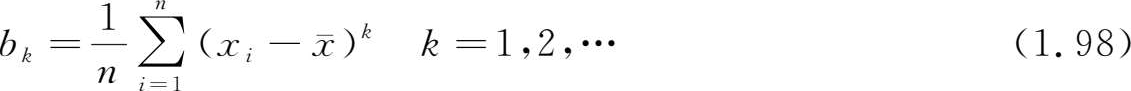
它们分别为下列随机变量的观测值
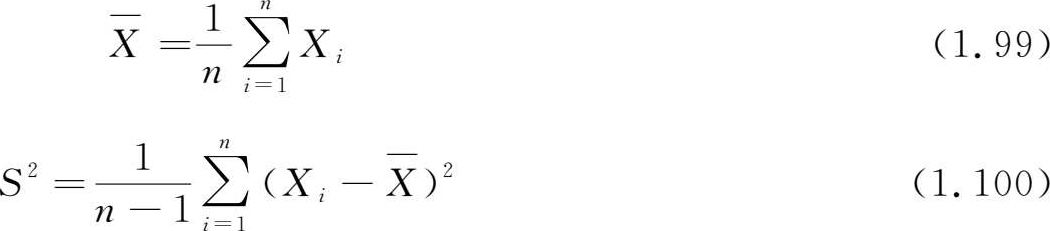
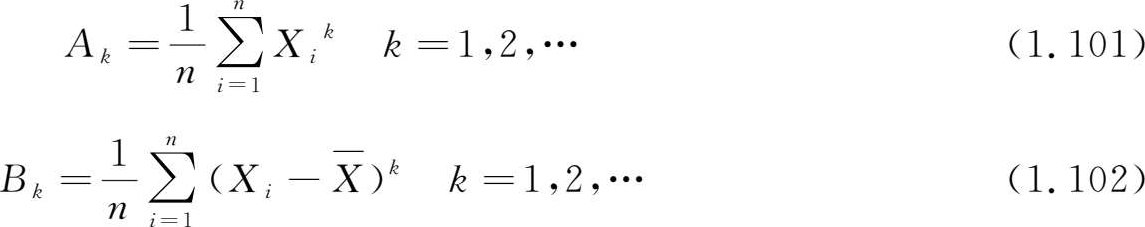
我们仍称这些随机变量为样本均值、样本方差、样本 k 阶矩及样本 k 阶中心矩,仅用字母的大小写来区别它们。
除此之外,由样本对总体的分布进行推断也是很重要的。一般的方法是通过统计观测值的频率分布来观察理论分布的概貌以及由样本观测值的频率直方图近似地描绘出分布密度曲线。
设 x 1 , x 2 ,…, x n 是某个天文量的 n 个观测值,将它们按由小到大的顺序排列为
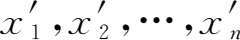
作出函数

则称 F n ( x )为观测值 x 1 , x 2 ,…, x n 的 经验分布函数 或 样本分布函数 (empirical distribution function)。对于不同的样本观测值,将得到不同的经验分布函数,但它们都是总体 X 分布函数 F ( x )的缩影。而随着样本容量 n 的增加,经验分布函数和理论分布函数之间的差别也愈来愈小。
除了用经验分布来描述观测值的分布外,也可以像概率分布一样用频率分布律或 频率 直方图 (frequency histogram)来描述观测值的分布。
设离散型随机变量的 n 个观测值为 x 1 , x 2 ,…, x n ,统计变量的各可能值出现的频数和频率,以横坐标表示各可能值,纵坐标表示各可能值出现的频率,并以平行于纵坐标的线段表示频率,这样得到的图形称为离散型随机变量的频率分布图。
若 x 1 , x 2 ,…, x n 为连续型随机变量的观测值,由连续型随机变量的概率性质可知,我们不应统计各个观测值出现的频率,而应统计它在某一范围内出现的频率。为此,我们把观测值的变化范围划分为许多连续但不重叠的区间,统计观测值落在各区间内的频率。每一小区间称为组;小区间的长度称为组距,以 h 表示;各区间的端点称为上、下组限;每一组的中点值称为组中值。下面我们给出用来描述连续型随机变量观测值的频率分布的频率直方图的绘制步骤:
(1)划分观测值的分组区间。找出观测值的最大值和最小值,并将观测值按自小到大的次序排列得 x' 1 , x' 2 ,…, x' n ,选取两个实数 a , b ,使它们尽量靠近 x' 1 和 x' n ,即 a ≤ x' 1 , b ≥ x' n 。把区间[ a , b ]分成 k 个互不相交的子区间。
(2)计算各组的频率。统计样本观测值落入每个子区间的个数 n k 。它就是这区间或这组的频数,并计算相应的经验频率 f k = n k / n 。
(3)作频率直方图。以区间序数为横坐标,经验频率为纵坐标得到频率直方图。这是一个由矩形阶梯组成的图形,矩形的宽等于组距 h ,矩形的高为各组频率。也有人将频率与组距之比看作矩形的高,这样每个长方形的面积刚好近似地代表了随机变量取值落入“底边”的概率。频率直方图上各组的中点的连线称为频率多边形,将频率多边形修匀可以得到一光滑曲线,即近似的分布密度曲线。容易看出,如果样本容量越大,分组越细,频率直方图就越接近随机变量的概率分布特征;但分组太多则不能抵消抽样的随机波动。
在实际应用中,常用频数代替经验频率做直方图的纵坐标,图1.9是太阳系小行星分布( a <6AU)的直方图[数据来自小行星中心(Minor Planet Center,MPC)]。从这个直方图中,可以清楚地看出小行星主要聚集在主带附近,受到不同大行星的摄动较多,分布较为复杂;在 a =5.2 AU处有一个明显的鼓包,这是木星的特洛伊小行星,主要受木星的摄动,因而由中心极限定理呈近正态分布。
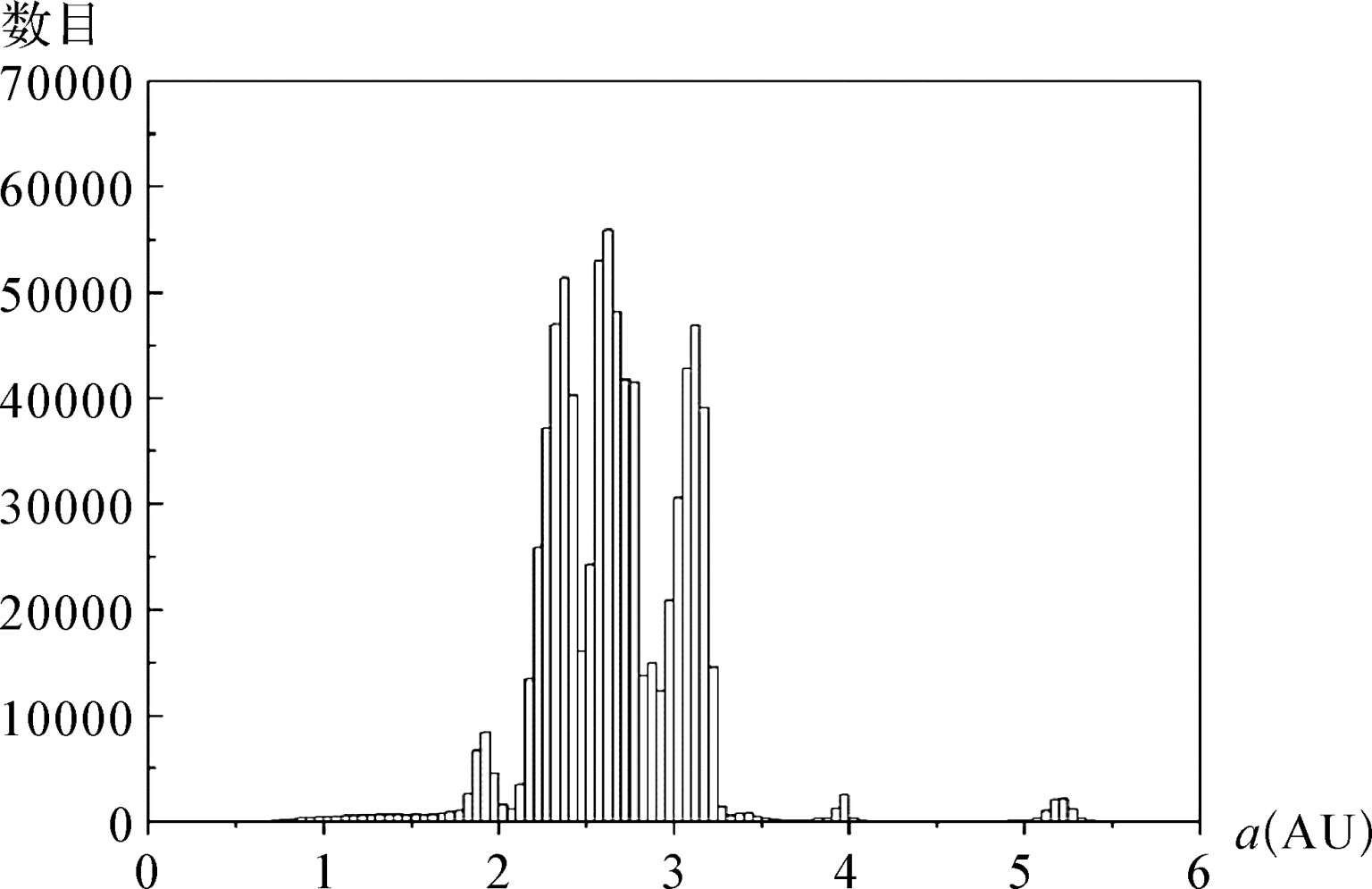
图1.9 太阳系小行星( a <6AU)的分布
在统计学中,当利用观测样本推断总体特征时,通常应从抽取的样本出发,把样本中所包含的我们关心的信息集中起来,针对不同问题构造样本的某种函数,由此获得统计推断的一般理论,然后把它应用到一个具体的样本中去。在数理统计中,称样本的函数为统计量。前面我们曾指出,样本是一个多维随机变量,因此,统计量也是随机变量,也有概率分布和数字特征。统计量的概率分布通常称为 抽样分布 (sampling distribution),而其数字特征就称为抽样分布的数字特征,研究抽样分布的性质是统计推断的重要内容。
统计量既然是样本的函数,那么它的分布也可以利用随机变量函数分布的理论得到。
下面介绍几种常用统计量的分布。为了避免混淆,仍以
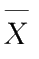 ,
S
2
表示随机变量
X
的样本均值、样本方差,而以
,
S
2
表示随机变量
X
的样本均值、样本方差,而以
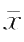 ,
s
2
表示样本观测值的均值和方差。
,
s
2
表示样本观测值的均值和方差。
抽样分布可以用数字特征来描述,其种类和定义完全与随机变量的数字特征相同,其中最常用的是抽样分布的数学期望和方差(均方差)。一般说来,求抽样分布的数字特征,需要知道统计量的分布。但对于一些特殊的统计量,可不必知道其分布。
1)样本均值的数学期望和方差
若( X 1 , X 2 ,…, X n )为取自数学期望为 μ ,方差为 σ 2 的总体 X 中的样本,则有
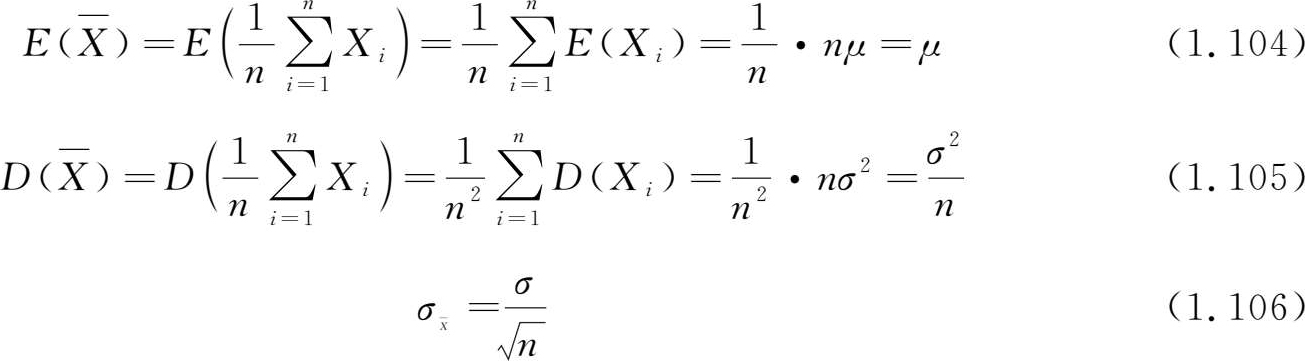
2)样本方差的数学期望
由定义(1.100)式,有
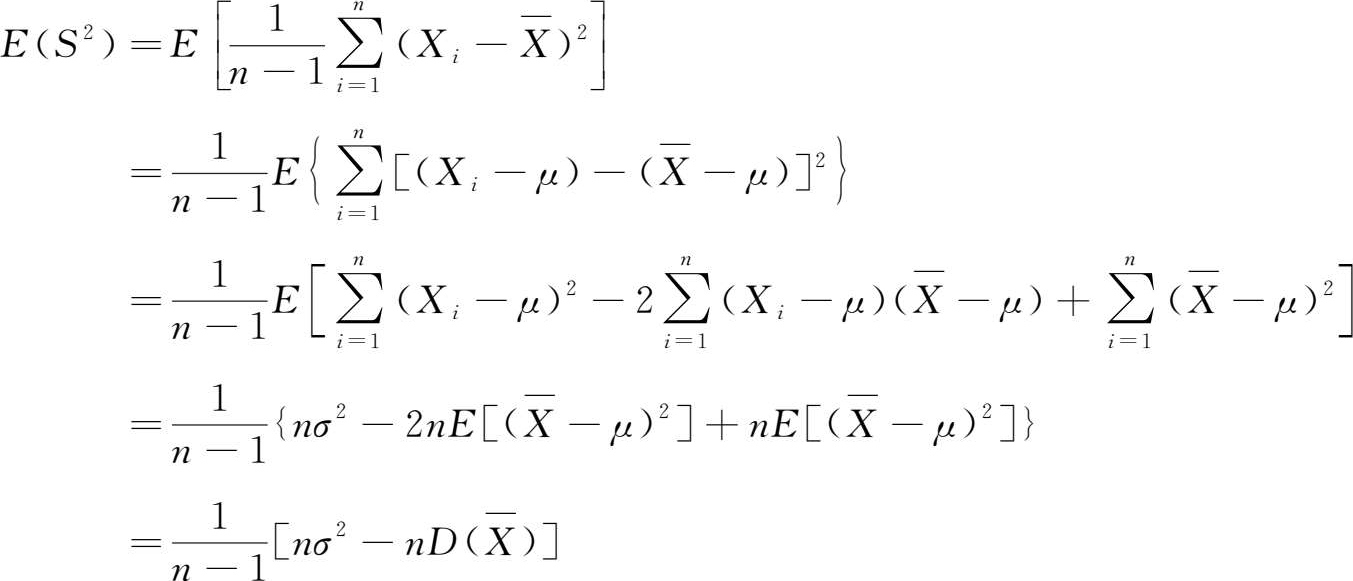
将(1.105)式代入,则得

从以上推导过程看出,上面几个式子对于任何分布的总体都是成立的。这里没有给出 S 2 的方差,它与总体分布形式有关。
1)来自正态总体的样本均值的分布
定理
1.1
设
X
~
N
(
μ
,
σ
2
),
X
1
,
X
2
,…,
X
n
为它的一个样本,则样本均值
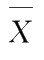 ~
~
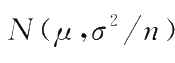 。
。
证明 :由(1.29)式知,若 X ~ N ( μ , σ 2 ),则
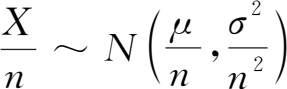
统计量
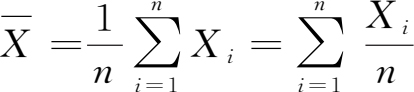
是
n
个相互独立的正态变量
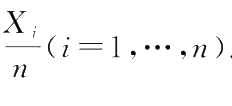 之和。利用例1.10的结论,可知
之和。利用例1.10的结论,可知
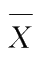 亦服从正态分布,且它的数学期望和方差分别是
亦服从正态分布,且它的数学期望和方差分别是
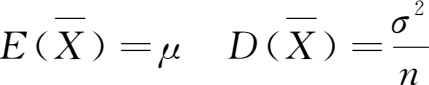
亦即

2) χ 2 分布和正态样本方差的分布
设 X ~ N (0,1), X 1 , X 2 ,…, X n 为 X 的随机样本,则它们的平方和 χ 2 服从参数为 n 的 χ 2 分布 (chi-square distribution),并记作 χ 2 ~ χ 2 ( n ), n 又称为 χ 2 分布的自由度。
χ 2 的概率密度函数为
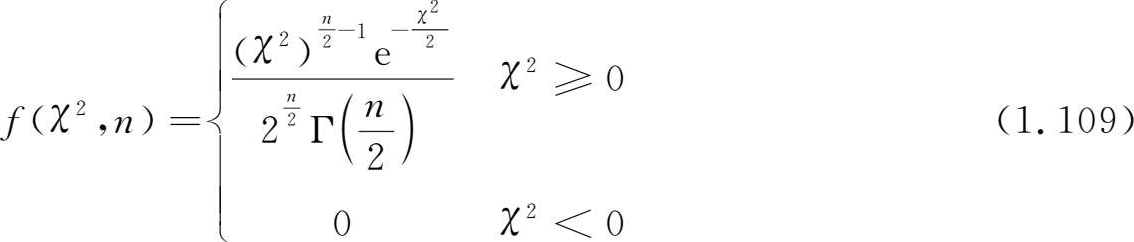
式中参数 n 为正整数,叫做 χ 2 的 自由度 (degree of freedom),表示 χ 2 是由 n 个相互独立的变量构成的;Γ( s )为Gamma函数,定义如下:
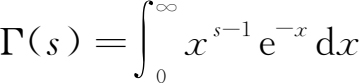
符号 χ 2 代表一个随机变量,常用 χ 2 ( n )表示自由度为 n 的 χ 2 分布。
容易证明,若统计量 χ 2 ~ χ 2 ( n ),则

图1.10中给出 n =1,4,10,20的 χ 2 分布密度曲线。 χ 2 分布在统计分析中有重要应用。为了应用的方便,给出对于各种自由度 n 及不同的概率 α 在满足以下关系式
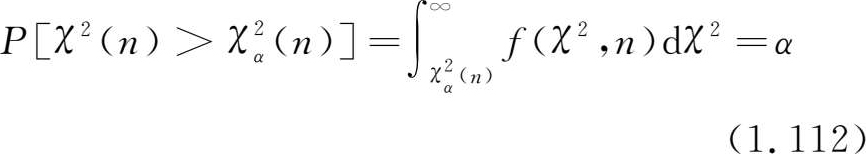
时的
χ
2
(
n
)值,并编制成
χ
2
分布表。当然也可以通过统计软件中的内置函数来求得。若
α
=0.05,
n
=30,可以查得
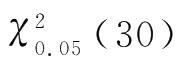 =43.77。当自由度
n
→ ∞时,
χ
2
分布接近于高斯分布。
=43.77。当自由度
n
→ ∞时,
χ
2
分布接近于高斯分布。
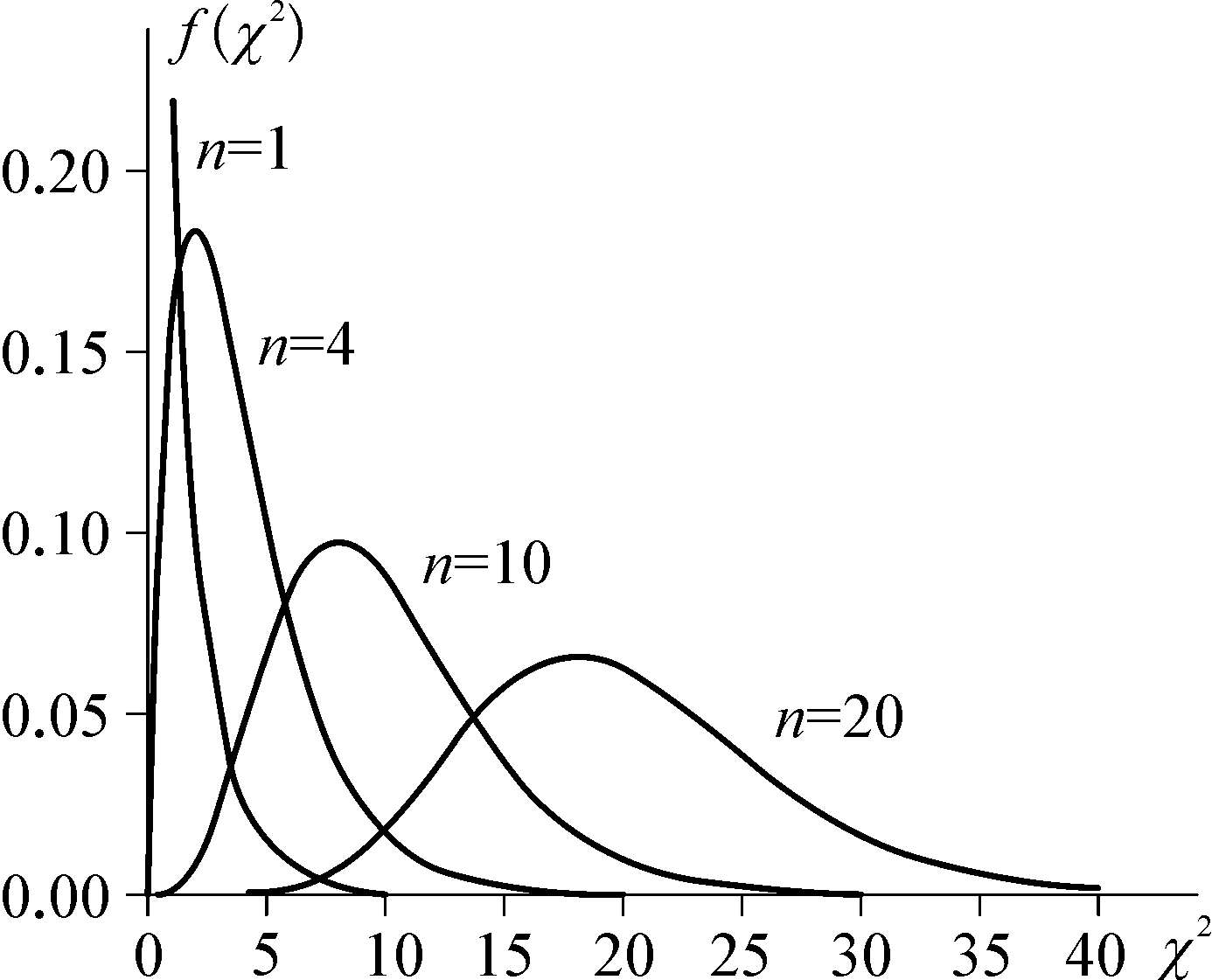
图1.10 χ 2 分布
下面我们给出和 χ 2 分布有关的定理,它们的证明从略。
定理 1.2 若 X ~ χ 2 ( n 1 ), Y ~ χ 2 ( n 2 ),且 X 和 Y 相互独立,则 X + Y ~ χ 2 ( n 1 + n 2 )。
定理 1.3 若 X ~ N ( μ , σ 2 ), X 1 , X 2 ,…, X n 为 X 的随机样本,则

有了这两个定理,我们就可以推导出正态样本方差的分布,即定理1.4。
定理 1.4 若 X 1 , X 2 ,…, X n 为正态总体 N ( μ , σ 2 )的随机样本。则有
(1)样本均值
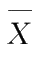 与样本方差
S
2
相互独立。
与样本方差
S
2
相互独立。
(2)统计量

证明 :
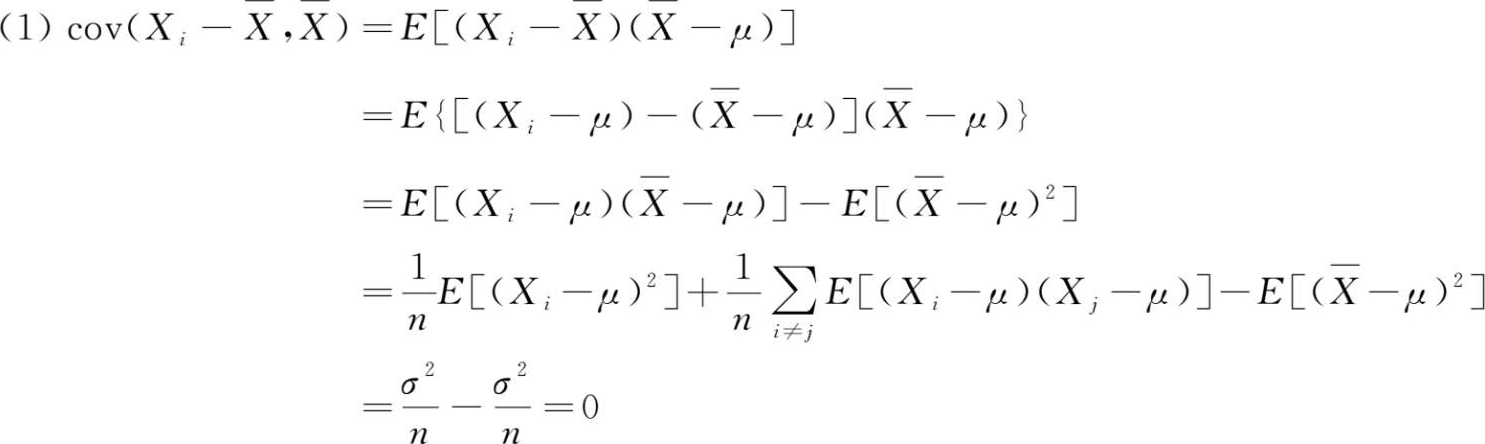
故有
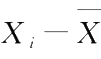 与
与
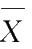 无关,又因
无关,又因
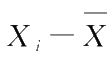 与
与
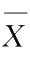 均服从正态分布,故
均服从正态分布,故
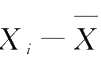 与
与
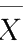 互相独立,而
互相独立,而
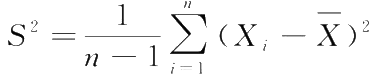 为
为
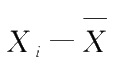 的函数,所以有
S
2
与
的函数,所以有
S
2
与
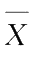 互相独立。
互相独立。
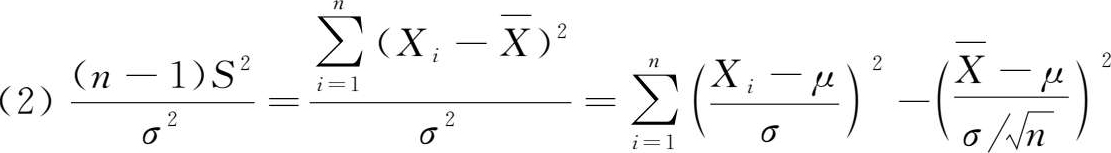
亦即
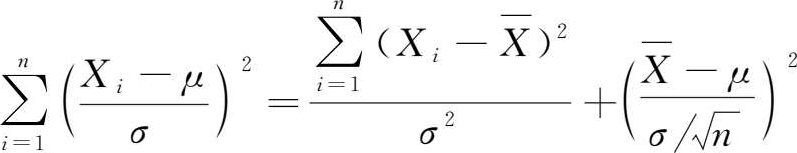
由定理1.3可知
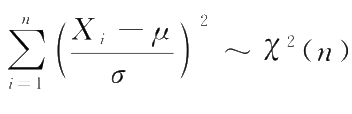 ,而
,而
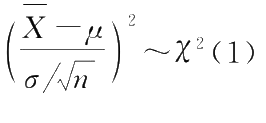
故由定理1.2得
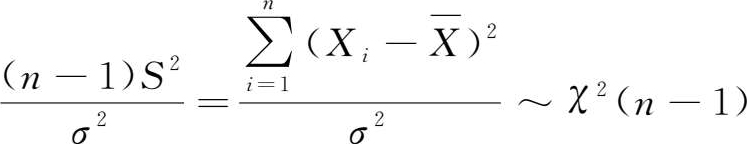
(1.113)式与(1.114)式的差别在于,(1.114)式中构成统计量的
n
个随机变量不完全独立,因为
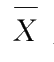 是由样本计算得到的,因此多了一个约束条件
是由样本计算得到的,因此多了一个约束条件
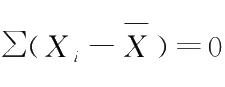 ,使得
χ
2
分布减少了一个自由度。
,使得
χ
2
分布减少了一个自由度。
统计量
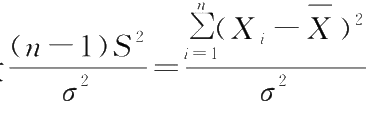 又常称作
χ
2
量,正态样本
χ
2
量的分布
χ
2
(
n
-1)同正态分布参数无关,只取决于样本容量
n
。所以利用样本
χ
2
量作统计推断比用样本方差更方便。
又常称作
χ
2
量,正态样本
χ
2
量的分布
χ
2
(
n
-1)同正态分布参数无关,只取决于样本容量
n
。所以利用样本
χ
2
量作统计推断比用样本方差更方便。
3) t 分布
设 X ~ N (0,1), Y ~ χ 2 ( n ),且 X 与 Y 相互独立,则称随机变量

服从自由度为 n 的 t 分布 ( t -distribution),并记作 t ~ t ( n )。
用求随机变量函数分布的方法,可以求出 t 分布的概率密函数式中 n 为 t 分布的自由度。
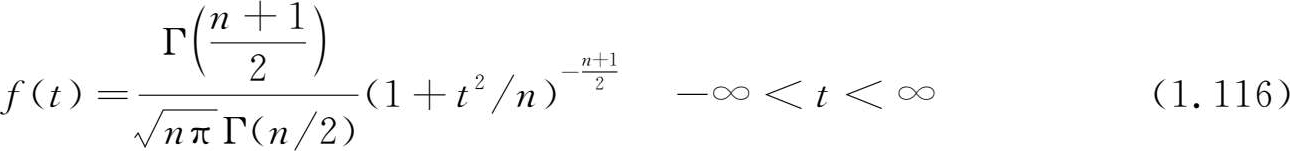
f ( t )的图形如图 1.11,它关于 t =0 是对称的。当 n →∞时, t 分布趋于标准正态分布。 t 分布表列出了对各个自由度 n 和 α' (0< α' <1)满足
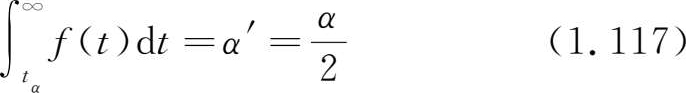
时的 t α ( n )值。
下面介绍几个和 t 分布有关的定理。它们是 t 分布的应用的重要依据。
定理 1.5 设 X 1 , X 2 ,…, X n 为正态总体 N ( μ , σ 2 )的一个样本,则统计量

其中
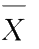 和
S
分别为样本均值及样本均方差,即
和
S
分别为样本均值及样本均方差,即
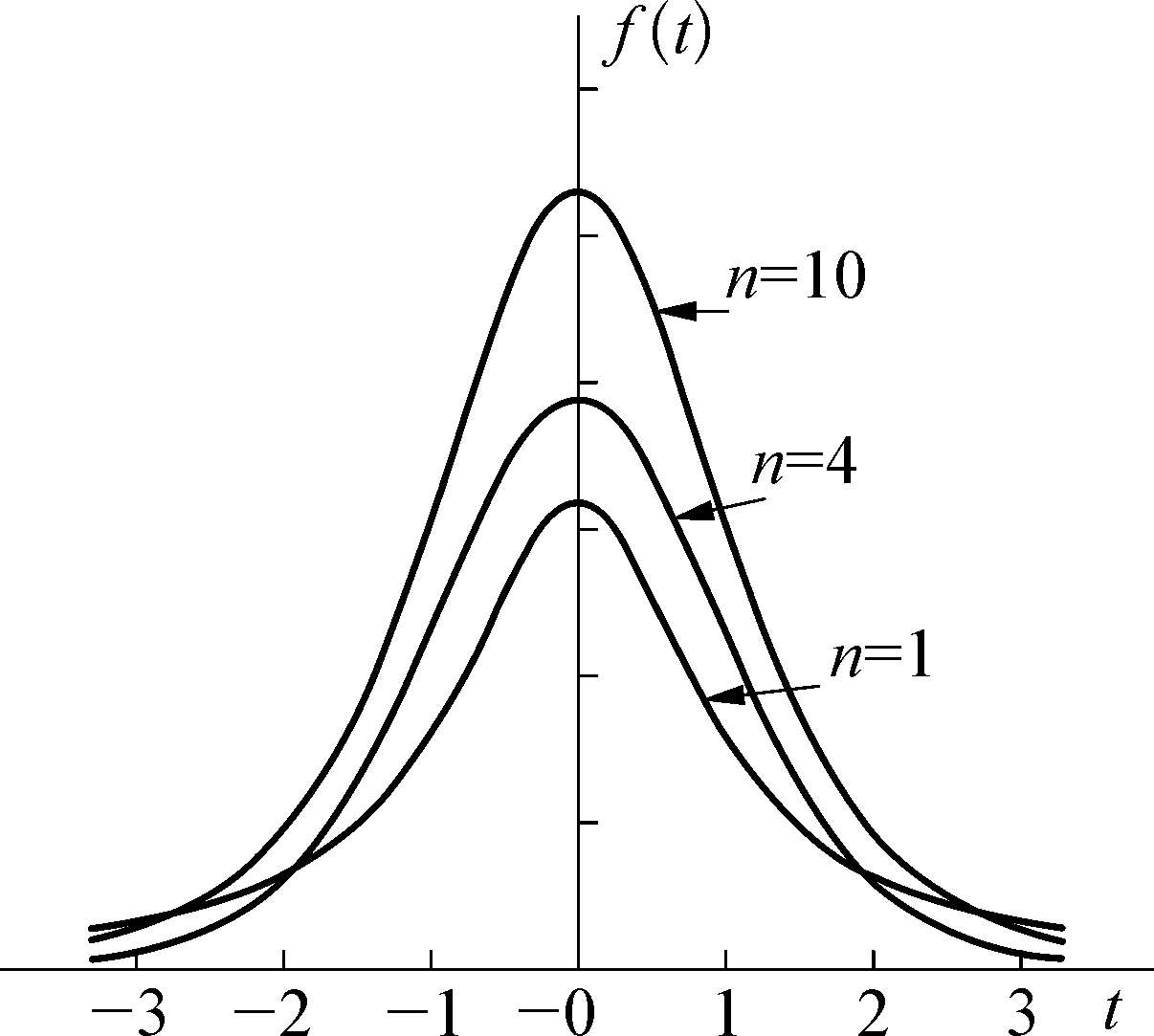
图1.11 t 分布
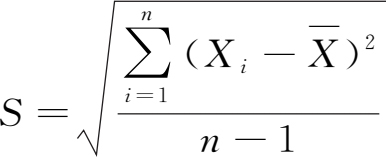
证明
:∵
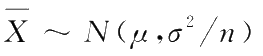
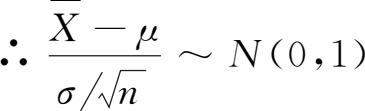
又由定理1.4知
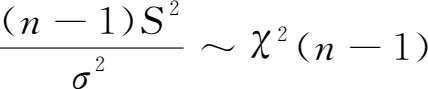
及
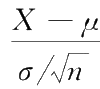 与
与
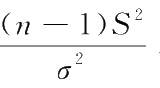 相互独立,故由
t
分布的定义得
相互独立,故由
t
分布的定义得
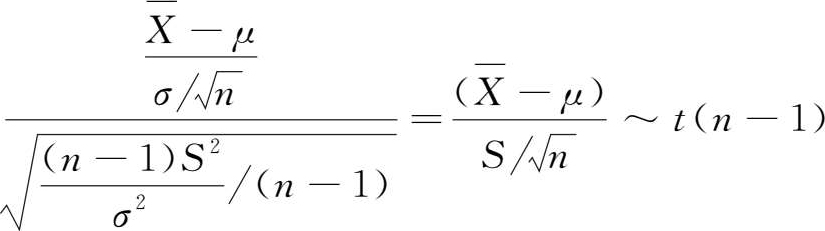
定理 1.6 设 X 1 , X 2 ,…, X n1 和 Y 1 , Y 2 ,…, Y n2 分别是正态总体 N ( μ 1 , σ 1 2 )和 N ( μ 2 , σ 2 2 )的随机样本,而且它们相互独立,则
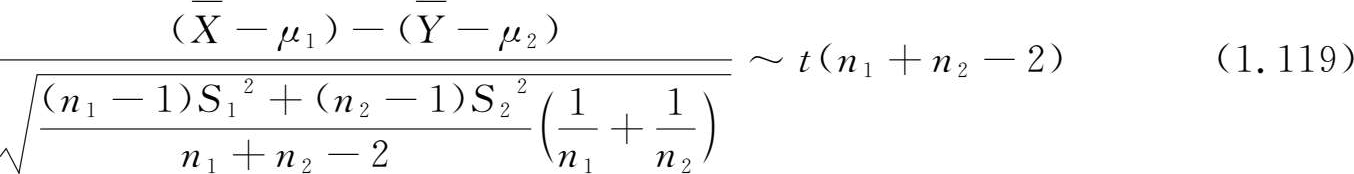
其中
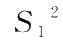 ,
,
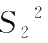 分别是
X
和
Y
的样本方差。
分别是
X
和
Y
的样本方差。
4) F 分布
设
X
~
χ
2
(
n
1
),
Y
~
χ
2
(
n
2
),并且
X
与
Y
相互独立,则称随机变量
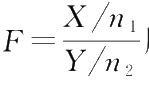 服从自由度为(
n
1
,
n
2
)的
F
分布
(
F
-distribution),即
服从自由度为(
n
1
,
n
2
)的
F
分布
(
F
-distribution),即

F分布的概率密度为
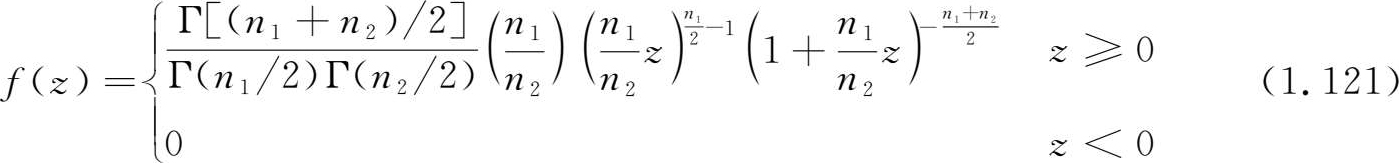
F 分布也是统计分析中非常重要的分布。和其他分布一样,也可对 F 分布列出对给定的 α =(0.01,0.05,0.1)及自由度 n 1 , n 2 ,当满足关系式
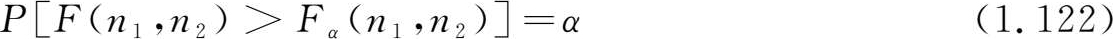
时的 F α ( n 1 , n 2 )数值,称为 F 分布表。对于表中没有列出的 n 1 , n 2 ,可以利用下列关系求得
