二项分布 (binomial distribution)来源于重复独立试验。将某一试验重复 n 次,若各次试验的结果互不影响,即每次试验结果出现的概率都不依赖于其他各次试验的结果,则称这 n 次试验是独立的。重复试验中最简单的是伯努利试验(Bernoulli trials),它可以描述为每次试验只有两个可能的结果 A 及 A , A 出现的概率为 p , A 出现的概率为 q =1- p 。假设重复进行 n 次试验,考虑 A 在 n 次试验中出现的次数 X 。显然,它是一个能取0,1,2,…, n 等整数值的离散型随机变量。下面讨论 X 的概率分布。先计算在 n 次试验中 A 出现 k 次的概率 P n ( k )。
假定事件
A
在某
k
次试验中出现,例如在第一次至第
k
次试验中出现。则在第
k
+1次至第
n
次试验中必出现
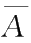 。因为试验是相互独立的,因此,事件
A
(1)
A
(2)
…
A
(k)
及
。因为试验是相互独立的,因此,事件
A
(1)
A
(2)
…
A
(k)
及
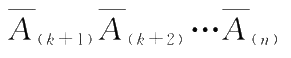 同时出现的概率为
同时出现的概率为
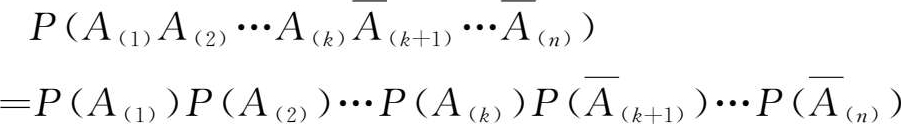
因为在各次试验中
A
或
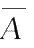 出现的概率保持不变,于是上式可写为
出现的概率保持不变,于是上式可写为
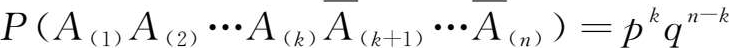
事实上,在
n
次试验中指定
k
次的方法有
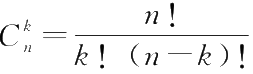 种,而且这些指定方法是互不相容的。在
n
次试验中
A
出现
k
次的事件是这些事件的总和,根据互不相容事件的概率加法定理可得
X
的概率函数为:
种,而且这些指定方法是互不相容的。在
n
次试验中
A
出现
k
次的事件是这些事件的总和,根据互不相容事件的概率加法定理可得
X
的概率函数为:

因为在 n 次试验中 A 的出现情况必然为0次、1次、…、 n 次中的一种,于是有
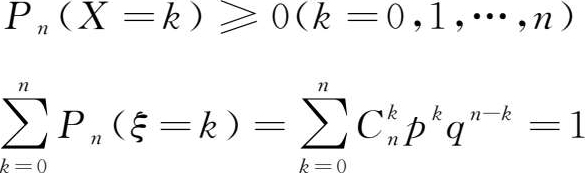
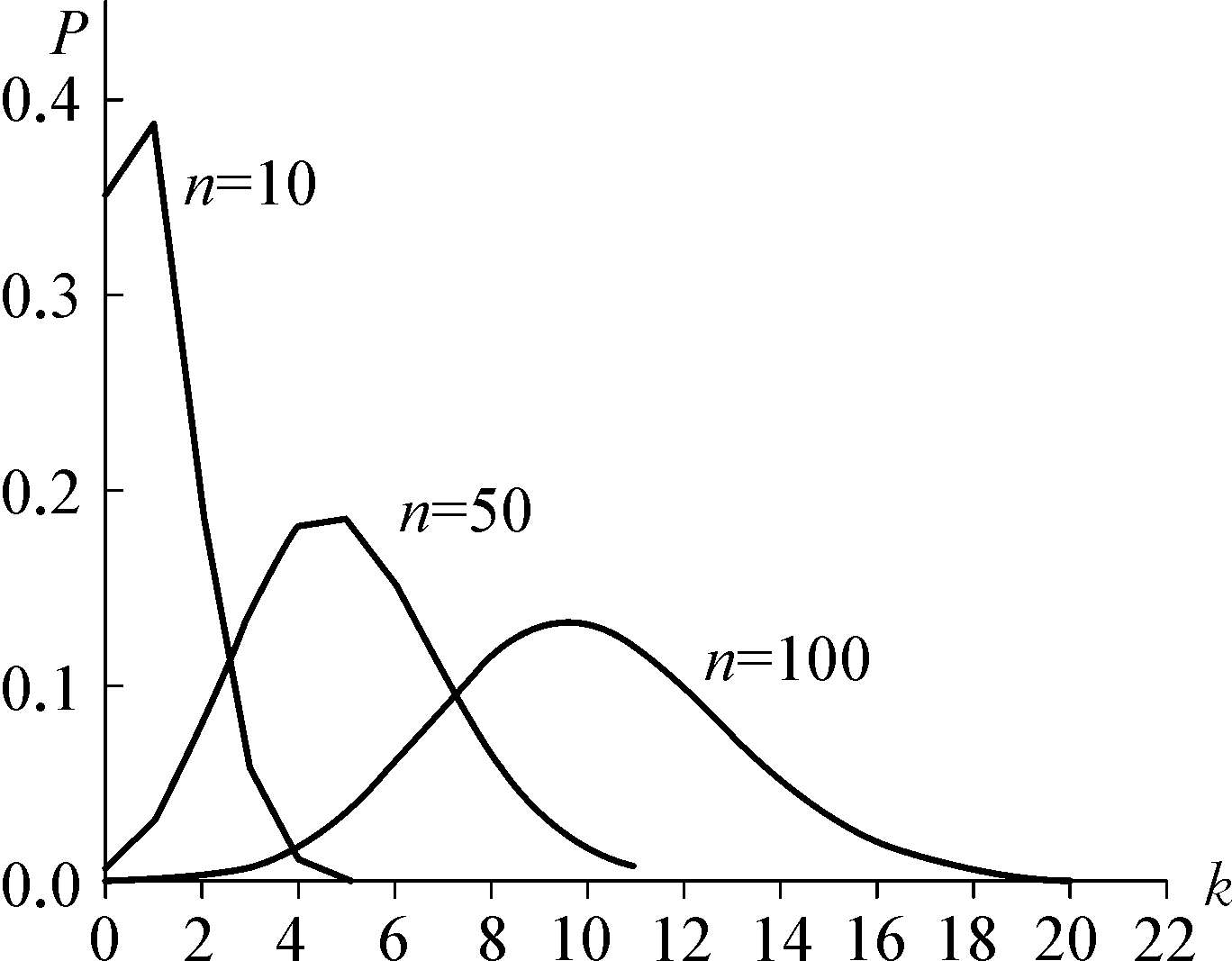
图1.7 二项分布
即 P n ( k )满足概率密度函数的条件。而(1.80)式刚好是二项式( p + q ) n 展开式的第 k +1项,因此称随机变量 X 服从参数为 n , p 的二项分布,记为 X ~ B ( n , p )。图1.7为二项分布的图形,由图中看出,当 n 增大时,二项分布趋于对称。
二项分布的分布函数为
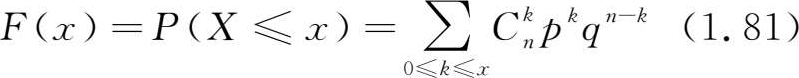
例 1.7 :某天文站进行人卫激光观测,设每次射击的命中率是0.2,独立观测10次,试求击中卫星的次数大于等于2的概率。
解 :将每次射击看作一次试验,设击中的次数为 X ,则 X 服从参数 n =10, p =0.2的二项分布,其分布律为
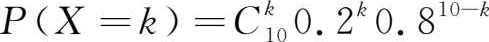
于是所求的概率为
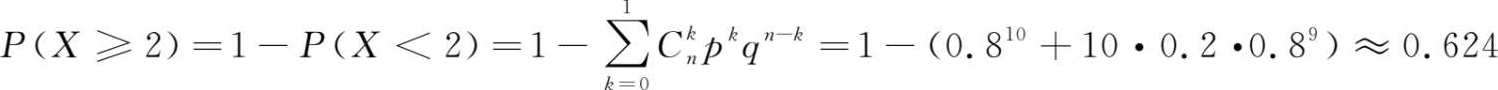
可以证明,二项分布随机变量的期望值为 np ,方差为 np (1- p )。
对于离散型随机变量 X ,若它的概率密度函数具有如下形式
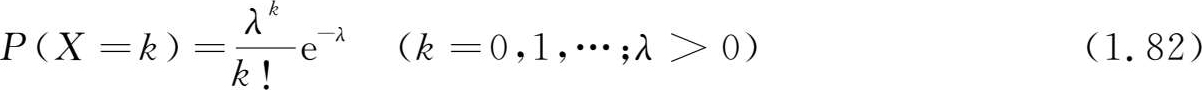
则称 X 服从 泊松分布 (Poisson distribution),式中 λ 为分布参数。
由(1.82)式,利用数学期望和方差的定义不难得到泊松分布随机变量的数学期望和方差,它们分别为 E ( X )= λ 和 D ( X )= λ 。
证:
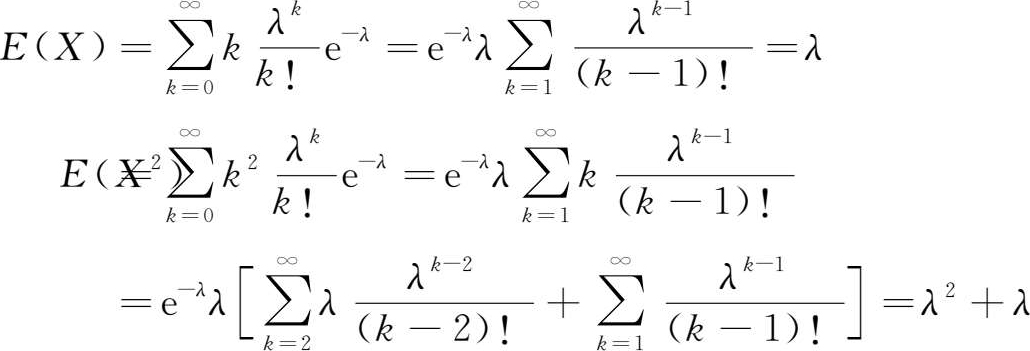
而 D ( X )= E ( X 2 )- E ( X ) 2 = λ 2 + λ - λ 2 = λ ,得证。
可以证明,泊松分布可看作 p →0, n →∞时二项分布的极限,且有 λ = np 。
服从泊松分布的随机变量在实际应用中有很多。例如,电话交换台一小时内收到的电话呼唤次数,不变天体发射出的光子到达时间。泊松分布也常用于描述小概率事件的统计规律。在天文、气象统计中,可用来描述流星、冰雹、龙卷风等现象的概率性质。
均匀分布 (uniform distribution)是最简单而又常用的分布。若随机变量 X 的概率密度为:
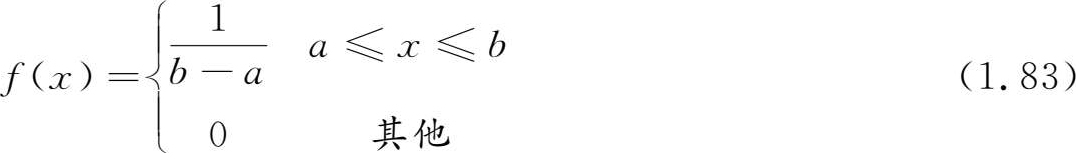
则称 X 服从区间[ a , b ]的均匀分布。
均匀分布的期望值和方差分别为:
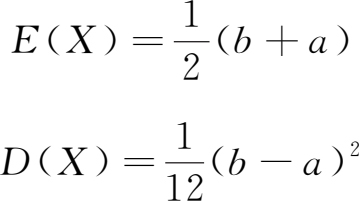
其分布函数的一般形式是
在区间[ a , b ]上的随机变量 X 在给定区间( α , β )内取值的概率为
常见的舍入误差(四舍五入)服从均匀分布。
实验工作中常用(0,1)区间均匀分布,其分布密度为
期望值、方差分别为1/2和1/12。
在[0,1]区间均匀分布的随机变量 X 通过变换
可以得到在[ a , b ]区间均匀分布的随机变量 Y 。利用随机变量函数分布的公式容易证明, Y 确实服从[ a , b ]区间的均匀分布。
实验设计中经常需要利用均匀分布的随机数,这种随机数可以用抽签、投骰子等办法产生。现代科学中,常用蒙特卡洛方法(Monte Carlo method)——随机现象的数学模拟方法,在计算机上产生各种分布的随机变量的样本,即随机数。
若随机变量 X 的概率密度函数为

其中 λ >0为常数,则称 X 服从参数为 λ 的 指数分布 (exponential distribution),可记为 X ~EXP( λ )。
由(1.84)式易得 X 的分布函数为
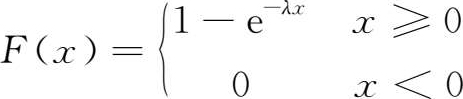
指数分布通常用作各种“寿命”分布,如电子元件的寿命、电话的通话时间等,因此它在可靠性理论与排队论中有广泛的应用。
正态分布是应用最广的一种分布,它最初由棣莫弗在求二项分布的渐近公式时得到。高斯在研究测量误差的分布时从另一角度导出了它,故将其命名为 高斯分布 (Gauss distribution)。高斯分布又叫 正态分布 (normal distribution),它的概率密度函数为
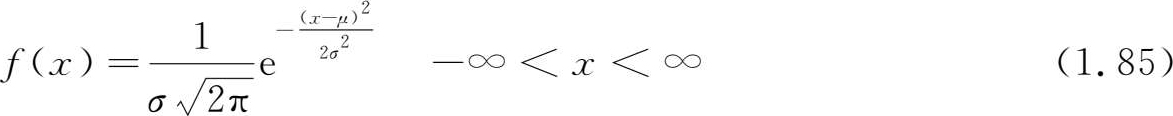
其中 μ 和 σ 2 为两个参数。
服从正态分布的随机变量 X 称为正态变量,通常记为 X ~ N ( μ , σ 2 )。
正态分布的分布函数为
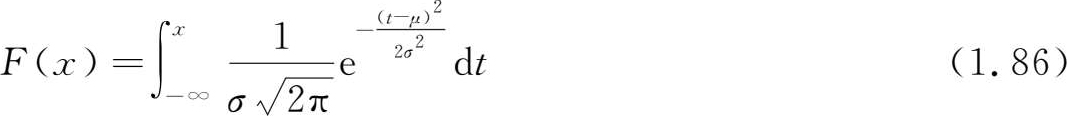
当 μ =0, σ 2 =1时,称 X 服从 标准正态分布 (standard normal distribution),记为 X ~ N (0,1)。其概率密度和分布函数分别为
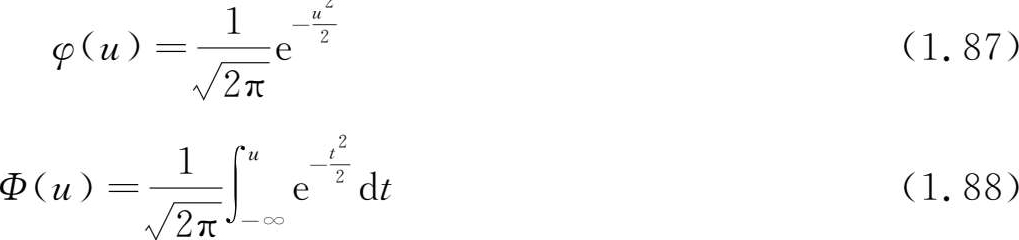
正态随机变量的数学期望和方差为
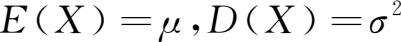
它们正好是正态分布的两个参数。
正态分布的概率密度曲线是单峰曲线,并且关于
x
=
μ
对称,在
x
=
μ
处有最大值
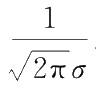 。参数
μ
决定分布的位置,而
σ
2
决定分布的宽窄;对于固定的
σ
,
f
(
x
)的位置随
μ
而变,对固定的
μ
,
f
(
x
)的形状随
σ
而变。图1.8给出不同参数值的正态密度曲线。
。参数
μ
决定分布的位置,而
σ
2
决定分布的宽窄;对于固定的
σ
,
f
(
x
)的位置随
μ
而变,对固定的
μ
,
f
(
x
)的形状随
σ
而变。图1.8给出不同参数值的正态密度曲线。
标准正态分布的分布函数数值可以通过标准正态分布表获得,也可利用统计软件中的内置函数求得。对于非标准正态分布的随机变量,则可通过变换
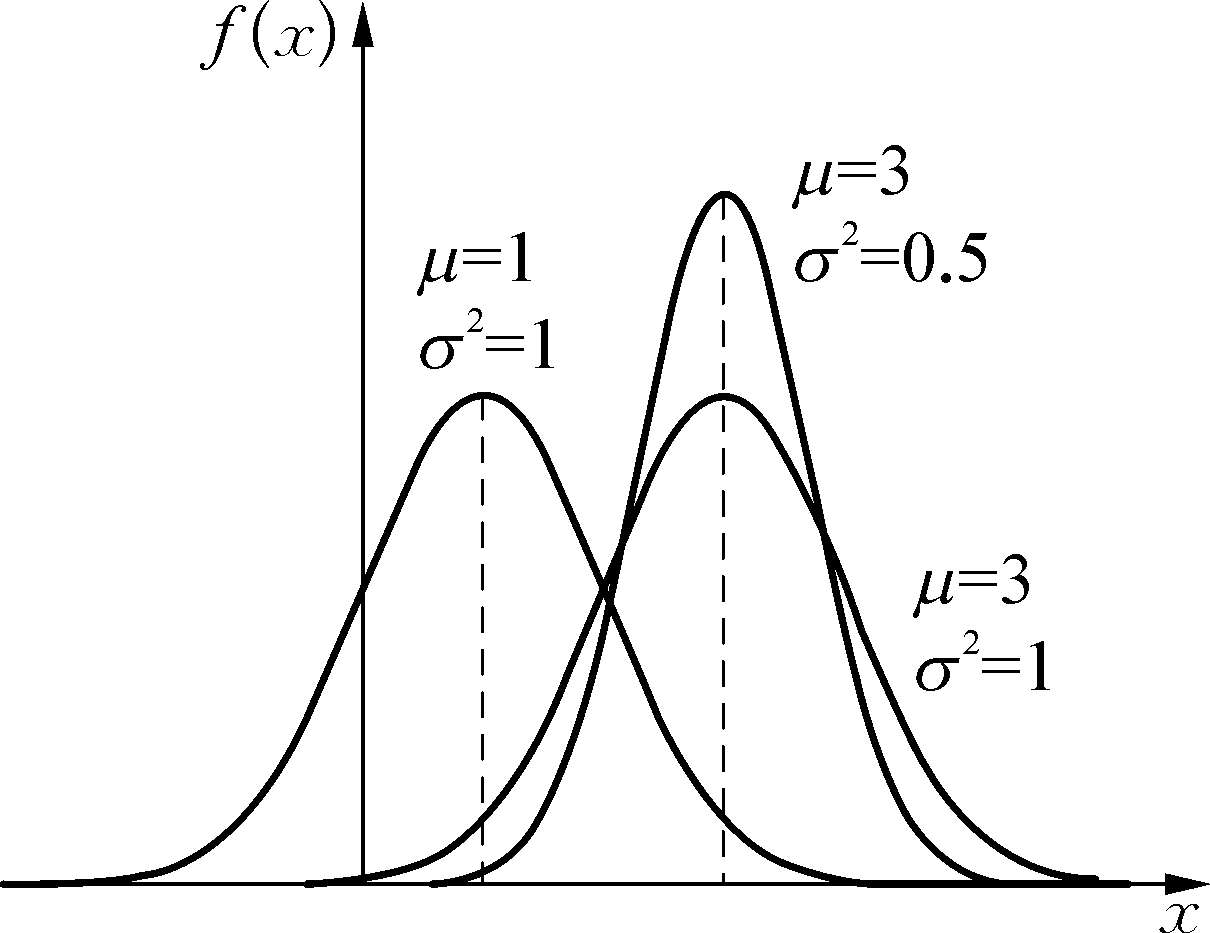
图1.8 高斯分布密度函数
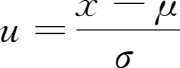
把它转化为标准正态分布,由(1.86)式有
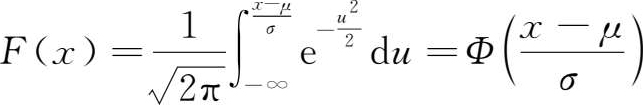
由于标准正态分布关于 y 轴是对称的,所以分布表中一般只列出 x ≥0的数,负值对应的分布函数值可利用对称性求得
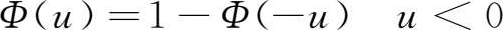
下面通过几个例子说明如何来计算正态变量的概率。
例 1.8 :已知 X ~ N (1,10 2 ),求 P ( X >12)及 P (5< X <10)。
解 :因为 P ( X >12) =1- P ( X <12) =1- F (12)
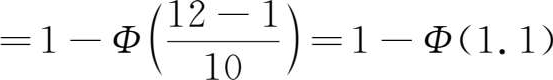
查正态分布表可得 Φ (1.1)=0.8643,于是
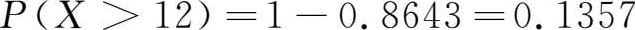
又
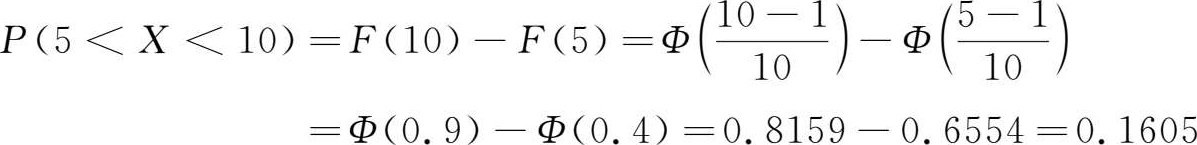
例 1.9 :已知 X ~ N ( μ , σ 2 ),求

解
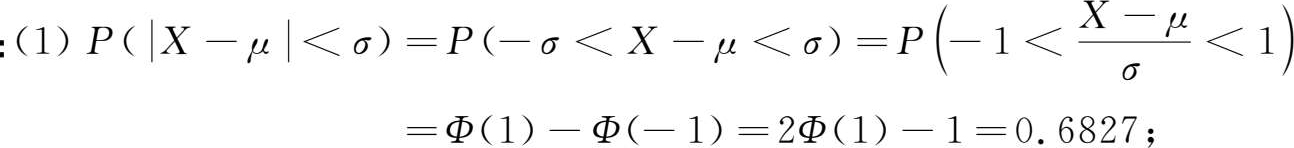
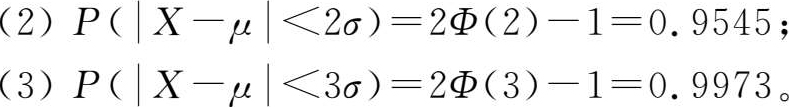
此例给出了正态变量 X 在期望值左右一倍、两倍和三倍标准误差范围内的概率含量。在实际数据处理中,还经常使用“2.6 σ 原则”,即测量误差在2.6倍均方差范围内的概率约为99%。
若二维随机变量( X , Y )的联合概率密度函数为
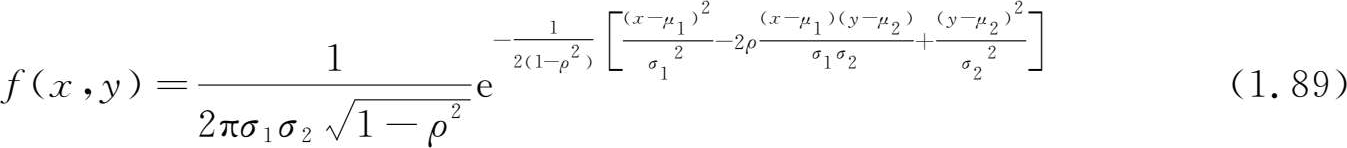
其中 σ 1 , σ 2 , μ 1 , μ 2 , ρ 均为常数,且 σ 1 >0, σ 2 >0,-1< ρ <1,则称( X , Y )为具有参数 μ 1 , μ 2 , σ 1 , σ 2 , ρ 的二维正态分布。
下面我们先求其两个边缘分布密度。
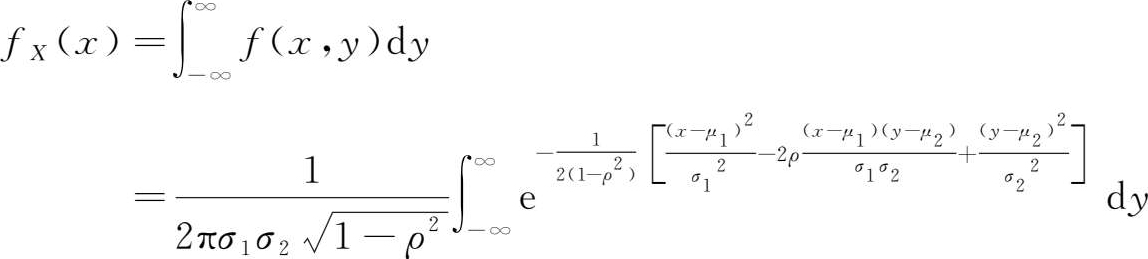
令
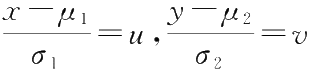 ,则
,则
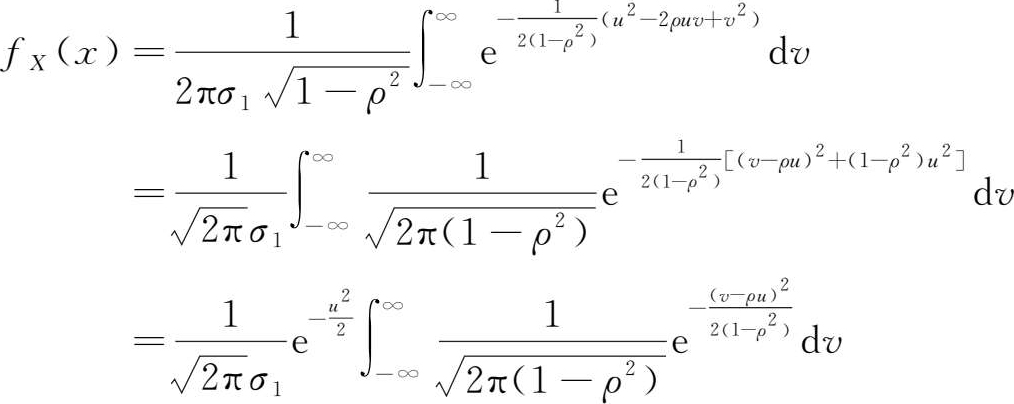
令
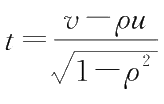 ,并利用
,并利用
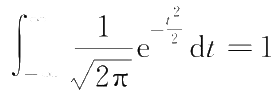 ,则
,则
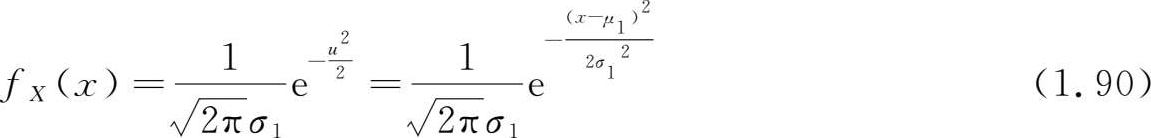
同理可得
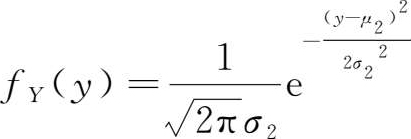
它们表明,二维正态分布的每一边缘分布都是服从正态分布的,并且都不依赖参数 ρ 。此外,不难证明 μ 1 , μ 2 和 σ 1 2 , σ 2 2 就是正态变量 X , Y 的数学期望和方差,还可以证明 X , Y 的协方差为
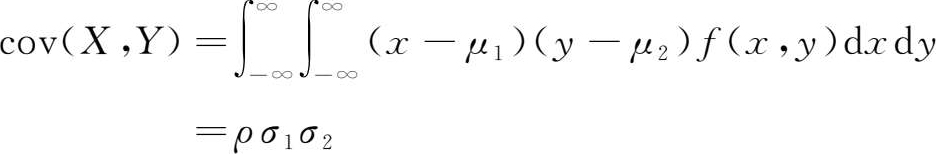
故有
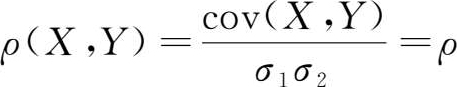
这就是说,二维正态分布概率密度中的参数 ρ 就是这两个正态变量的相关系数。在上一节相关系数的第3个性质中已经指出,若两个随机变量相互独立,则相关系数等于0,但反之并不成立,而对于两个正态变量,如果它们不相关,即 ρ =0,由(1.89)式有
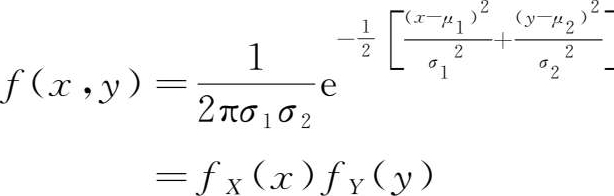
这满足随机变量独立性的条件。这说明,对二维正态随机变量( X , Y )来说,它们不相关与相互独立是等价的。
例 1.10 :设 X 和 Y 为两个相互独立的随机变量,且都具有 N (0,1)分布,求 Z = X + Y 的分布。
解 :由题意
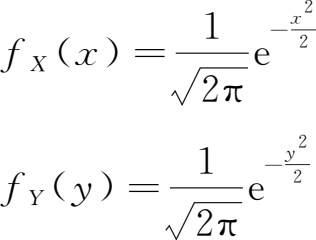
利用两个随机变量和的概率密度公式(1.58)及随机变量独立性条件,有
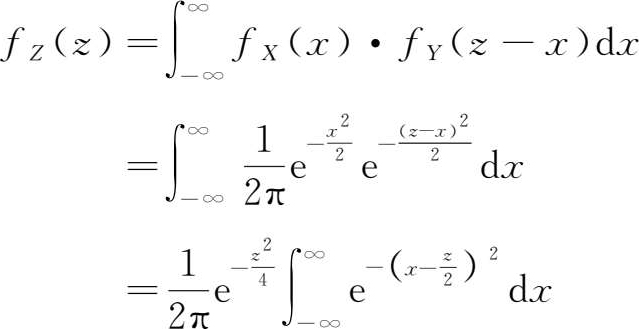
令
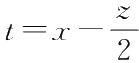 , 得
, 得
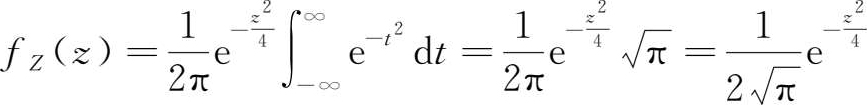
即
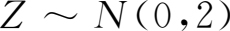
由此可以看出,相互独立的正态变量的和仍然具有正态分布,即若
X
,
Y
相互独立,且
X
~
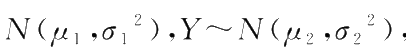 则
则
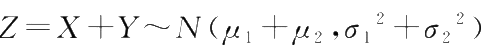 。这个结论还能推广到
n
个独立的正态变量之和的情况。
。这个结论还能推广到
n
个独立的正态变量之和的情况。
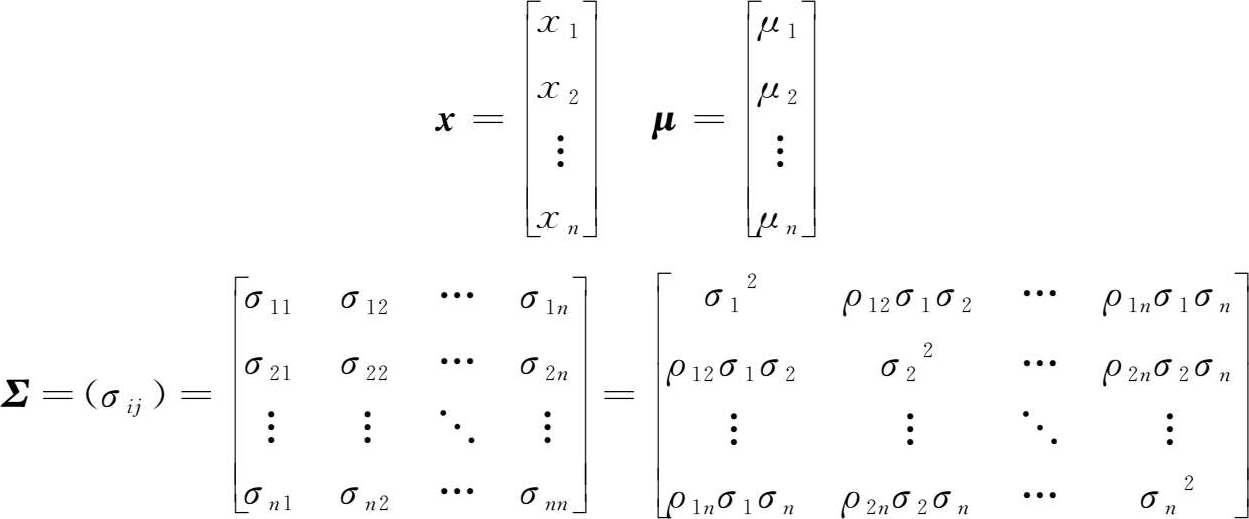
利用向量和矩阵,对二维正态分布进行改写。设
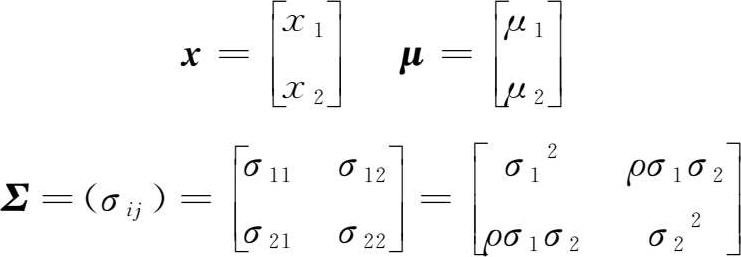
则二维正态分布可以写成
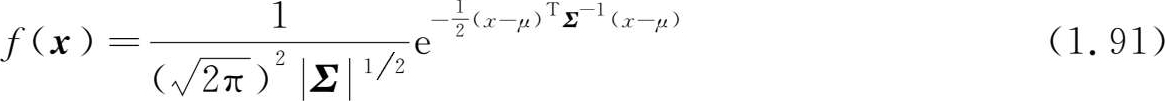
式中上标T表示矩阵的转置(transpose),
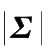 是矩阵(
σ
ij
)的行列式
是矩阵(
σ
ij
)的行列式
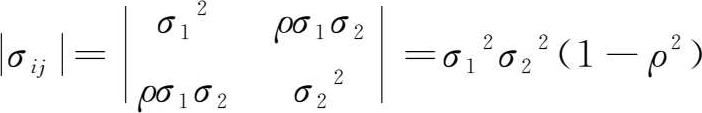
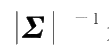 是(
σ
ij
)的逆矩阵。
是(
σ
ij
)的逆矩阵。
利用矩阵写法,不难将二维正态分布推广到多维正态分布,即 n 维正态分布的联合概率密度函数为
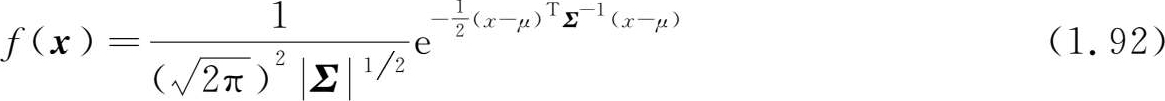
式中, x 为 n 维随机向量, μ 为 n 维实向量。