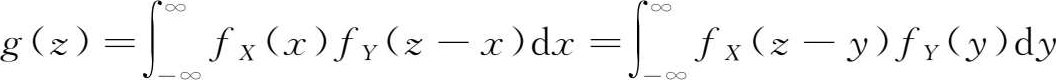如果在一个随机试验中,需要考虑两个或两个以上的随机变量,那么这几个随机变量就组合成一个多维随机变量。这种多维随机变量的概率性质,不仅与其中每一个分量的概率性质有关,还依赖于各分量之间的相互关系。
正如把一维随机变量比作数轴上的随机点一样,为了直观地解释多维随机变量的分布,我们可以把多维随机变量比作多维空间中的随机点。例如把二维随机变量( X , Y )视作平面上的点。当然,也可以把多维随机变量看作多维空间中的向量。因此,也称多维随机变量为随机向量。
设( X , Y )为二维随机变量(bivariate random variable),其分布函数定义为
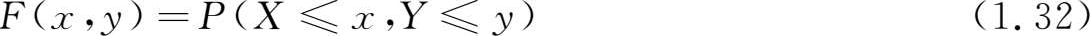
并称其为二维联合分布函数。
若将二维随机变量( X , Y )比作平面上点的坐标,则二维联合分布函数 F ( x , y )就是随机点落在图1.5中阴影部分的概率。
分布函数 F ( x , y )具有如下的基本性质:
(1) F ( x , y )是 x , y 的非降函数,即对于任意固定的 y ,当 x 2 > x 1 时, F ( x 2 , y )≥ F ( x 1 , y );对于任意固定的 x ,当 y 2 > y 1 时, F ( x , y 2 )≥ F ( x , y 1 )。
(2)0≤ F ( x , y )≤1,且对于任意固定的 y , F (-∞, y )=0,对于任意固定的 x , F ( x ,-∞)=0。并且有 F (-∞,-∞ )=0, F (+∞,+∞)=1。
图1.5 二维分布函数
若二维随机变量( X , Y )可取二维空间中某区域中的一切值,而分布函数 F ( x , y )连续,且有连续的二阶混合偏导数
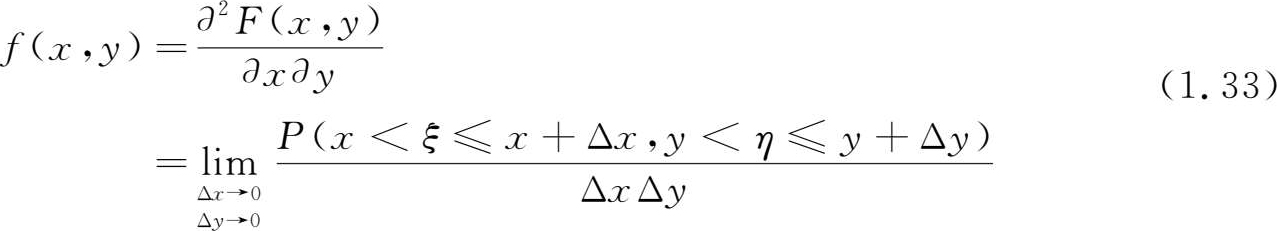
则称 f ( x , y )为( X , Y )的 联合概率密度函数 (joint probability density)。
和一维随机变量一样,分布函数 F ( x , y )也可用概率密度函数 f ( x , y )来表示,即
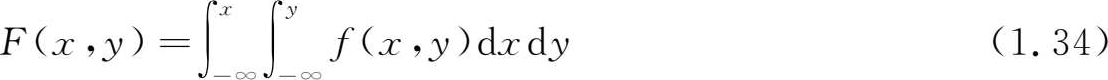
根据定义,概率密度 f ( x , y )具有以下性质:
(1) f ( x , y )≥0;
(2)
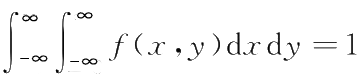 ;
;
(3)设 G 为 xoy 平面上的一个区域,点( X , Y )落在 G 内的概率为
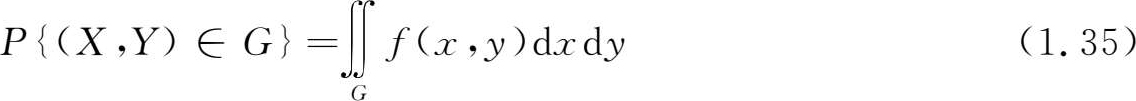
在几何上, f ( x , y )表示空间的一个曲面,称它为分布曲面。由性质(2),介于分布曲面和 xoy 平面之间的空间区域的全部体积等于1;由性质(3),随机向量( X , Y )在 xoy 平面上任意区域 G 内取值的概率等于以 G 为底,以曲面 f ( x , y )为顶面的柱体体积。
二维随机变量( X , Y )作为一个整体,它具有分布函数 F ( x , y )。而 X , Y 本身又都是随机变量,也有各自的分布函数,分别记为 F X ( x ), F Y ( y ),并依次称它们为二维随机变量关于 X 和关于 Y 的 边缘分布函数 (marginal distribution function),它们可以由( X , Y )的分布函数 F ( x , y )来确定,即
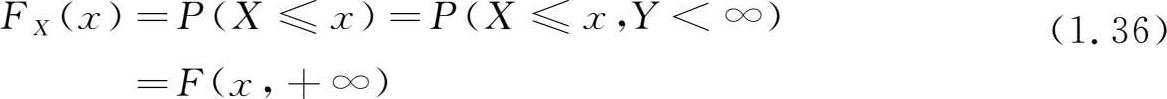
就是说,只要在函数 F ( x , y )中令 y →+∞,就能得到 F X ( x )。同理

由(1.34)式,边缘分布函数又可表示为
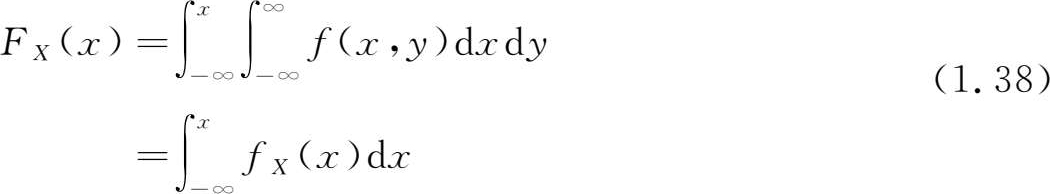
式中

为 X 的 边缘密度 (marginal distribution density)。同理有
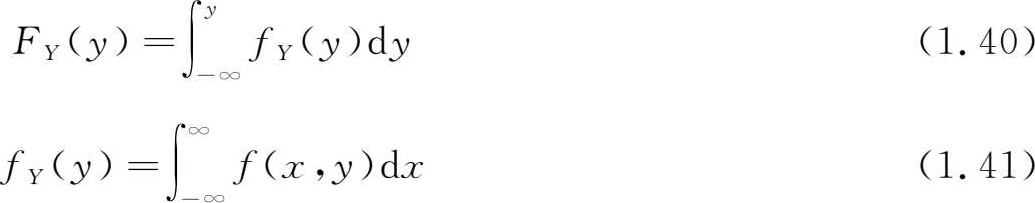
如果二维随机变量( X , Y )的所有可能取的值是有限对或可列无限多对,则称( X , Y )是二维离散型随机变量。
设二维离散型随机变量( X , Y )所有可能取的值为( x i , y j )( i , j =1,2,…),则称
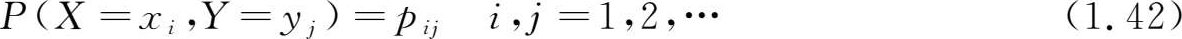
为二维离散型随机变量( X , Y )的概率分布或分布律,或之称为随机变量 X 和 Y 的 联合分布 律 (joint distribution law)。而 X 和 Y 的联合分布函数为

其中和式是对一切满足 x i ≤ x , y j ≤ y 的 i , j 来求和的。( X , Y )关于 X 和关于 Y 的边缘分布律分别为
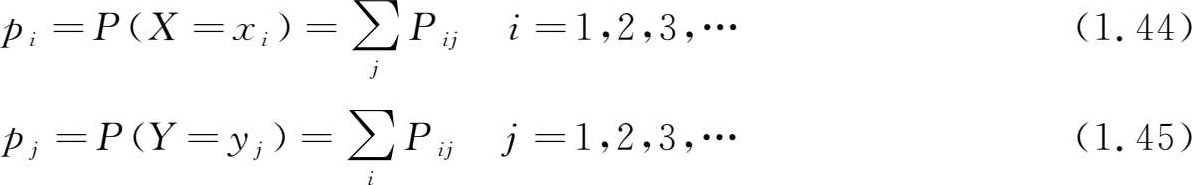
下面我们利用二维随机变量的分布函数及边缘分布函数的概念引出两个随机变量相互独立的概念。
设 F ( x , y )及 F X ( x ), F Y ( y )是二维随机变量( X , Y )的分布函数及边缘分布函数。若对于所有的 x 和 y 有

则称随机变量 X 和 Y 是 相互独立 的(mutually independent)。由分布函数和概率密度之间的关系,独立性条件也可用概率密度来表示,即

由随机事件的条件概率公式(1.9)可以得到随机变量 Y 对于 X 的 条件概率密度 公式(conditional probability density function)

同理有

比较(1.48)式(或(1.49)式)与(1.47)式可知, X 和 Y 相互独立的条件亦可表示为

或

若两个随机变量 X , Y 的分布不满足(1.46)至(1.53)各式,则它们是不独立的。
可以证明,若 X 和 Y 是相互独立的随机变量,则 X 的函数 φ ( x )和 Y 的函数 ψ ( y )也是相互独立的(只要利用(1.29)式和(1.47)式即可证)。
假设一个随机试验的结果需用 X 1 , X 2 ,…, X n 这 n 个随机变量来表示,则此多维随机变量可记成向量 X =( X 1 , X 2 ,…, X n ),并称 X i 为第 i 个分量。 n 维随机变量的分布函数(或称 n 个随机变量的联合分布函数)定义为
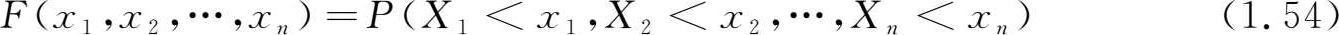
其中 x 1 , x 2 ,…, x n 为任意实数。
任意一个分量 X i 的边缘分布函数为
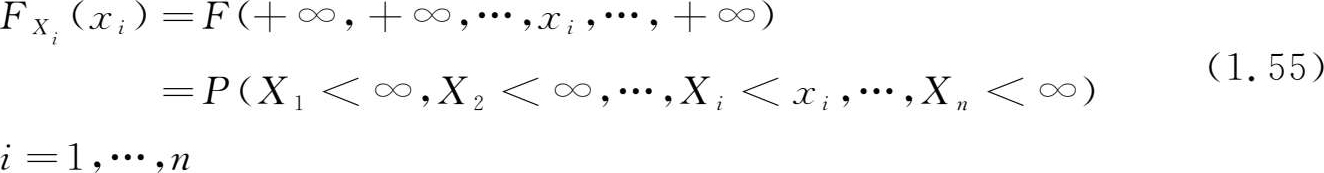
若 X =( X 1 , X 2 ,…, X n )可取 n 维空间中某区域上的一切值,且分布函数连续并有连续的 n 阶混合偏导数则称 f ( x 1 , x 2 ,…, x n )为 n 维随机变量的联合分布密度。
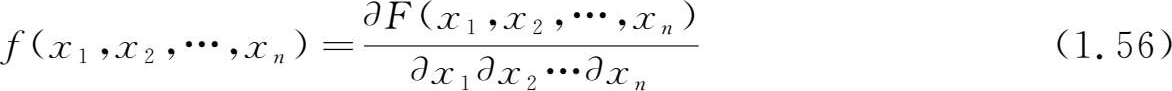
前面关于二维随机变量的所有公式都可以推广到 n 维随机变量的情况中。例如,若 n 维随机变量的联合分布函数可表为各分量 X i 的边缘分布函数 F X i (x i )的乘积,即
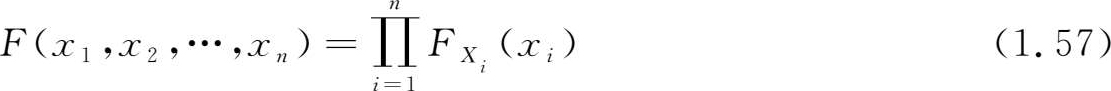
则称 n 个随机变量 X 1 , X 2 ,…, X n 是相互独立的。
下面我们再以 Z = X + Y 为例,讨论一下两个随机变量的函数的分布。
设二维随机变量( X , Y )的联合概率密度为 f ( x , y ),我们来求 Z = X + Y 的概率密度 g ( z )。
因为事件( Z < z )等价于事件(-∞< X <∞,-∞< Y < z - x ),因此 Z 的分布函数为
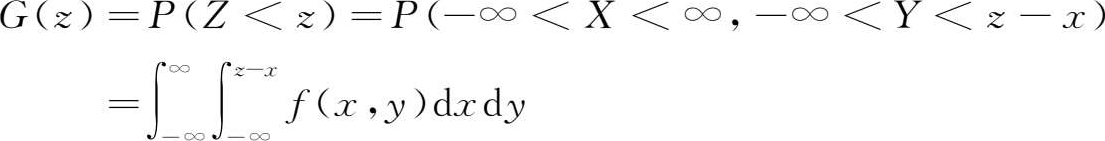
对 z 微分得 Z 的概率密度
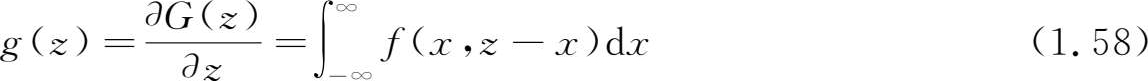
由 x 和 y 的对称性有
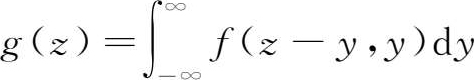
当 X 和 Y 独立时,因为 f ( x , y )= f X ( x )· f Y ( y ),故有