Q矩阵理论是描述属性及属性间层级关系、建立属性和题目之间关联,以及确定学生知识结构的理论体系。该理论的先驱Tatsuoka认为,Q矩阵理论旨在确定学生不可直接观察的知识结构,并运用可以直接得到的观察反应模式表示这些知识结构。学生的知识结构是由属性组成的向量表征。Q矩阵理论主要包括:属性层级结构(Attribute Hierarchy Structure,AHS)、邻接矩阵(Adjacency matrix,Q)、可达矩阵(Reachability matrix,Q)、缩减矩阵(Reduced Q-matrix,Qr)、测验Q矩阵(Test Q-matrix,Qt)、知识状态(Knowledge State,KS)等。以图3.1中B结构为例,对Q矩阵理论进行阐述。
图3.1B表示某测验界定的6个属性存在发散型层级关系,根据该结构,可以得到邻接矩阵A阵,它是描述属性间直接关系的K*K维方阵(K为属性个数),即表征了具有先后顺序的属性间的关系,如表3.1左侧所示。由A阵与同阶单位阵I的和A+I,通过Warshall算法可得到可达矩阵R阵,它是描述属性间直接、间接和自身关系的矩阵,如表3.1右侧所示。
表3.1 图3.1B结构下的邻接矩阵A阵及可达矩阵R阵
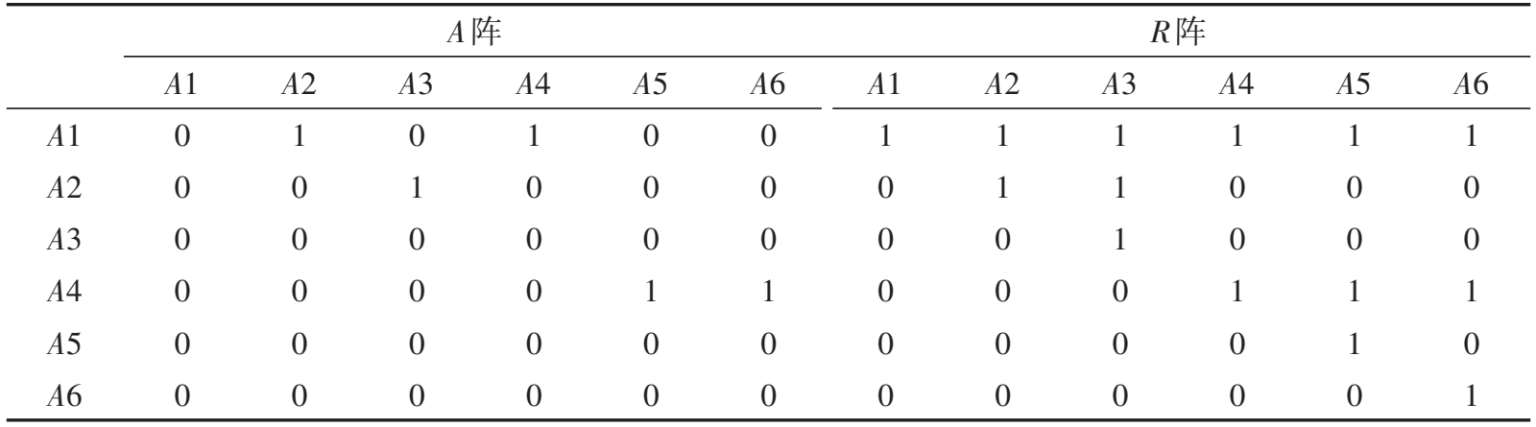
注:A1—A6表示图3.1B中的6个属性,“1”表示存在关系,“0”表示不存在关系。
在得到 R 阵之后,可通过删除法(Tatsuoka,1995)或扩张算法(杨淑群 等,2008)推出所有可能存在的项目类别,即该结构下的测验能够编制出来的所有题目类型,如表3.2所示。其中,行代表属性,列代表典型题目类,该矩阵即为缩减矩阵Qr。在该属性结构中,最多只能出15种类型的题目。
表3.2 图3.1B结构下的缩减矩阵Qr阵
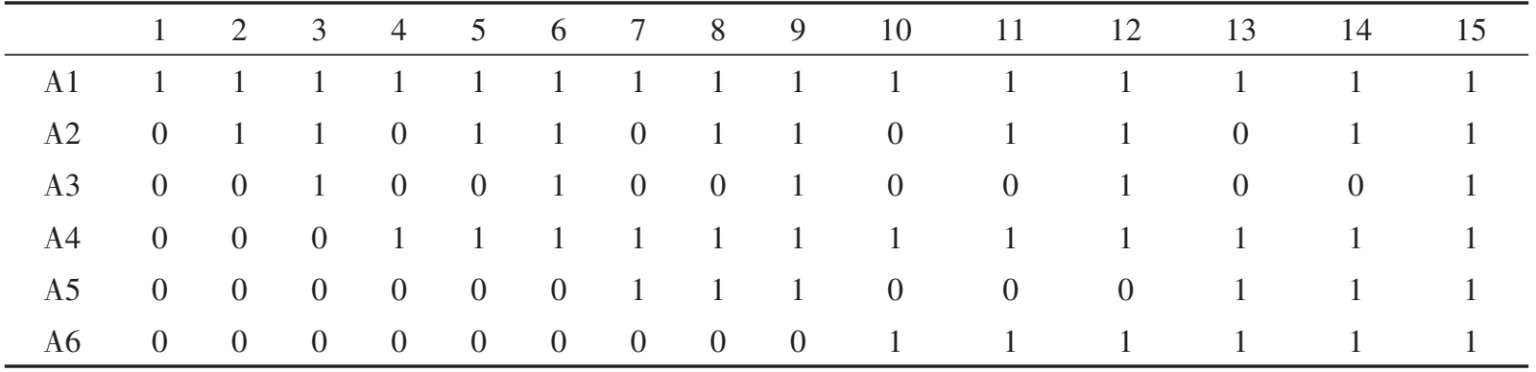
注:“1”表示题目考查了该属性,“0”表示题目没有考查到该属性。
在实际编制测验时,不要求涉及所有类型的题目,且通常来说,编制一道同时考查较多属性的题目较为困难。因此,就会存在某类型题目出现多次的情况,例如同时存在多道类型 2[110000]的题目,将这种实际测验所表示的 Q 阵记作 Qt 阵。丁树良等人(2012)证明过,若采用0-1评分方式且属性对认知任务所起的作用是非补偿连接的,则期望反应模式集合与知识状态集合建立起双射(bijective)的充分必要条件是可达阵 R 是 Qt 的子矩阵。
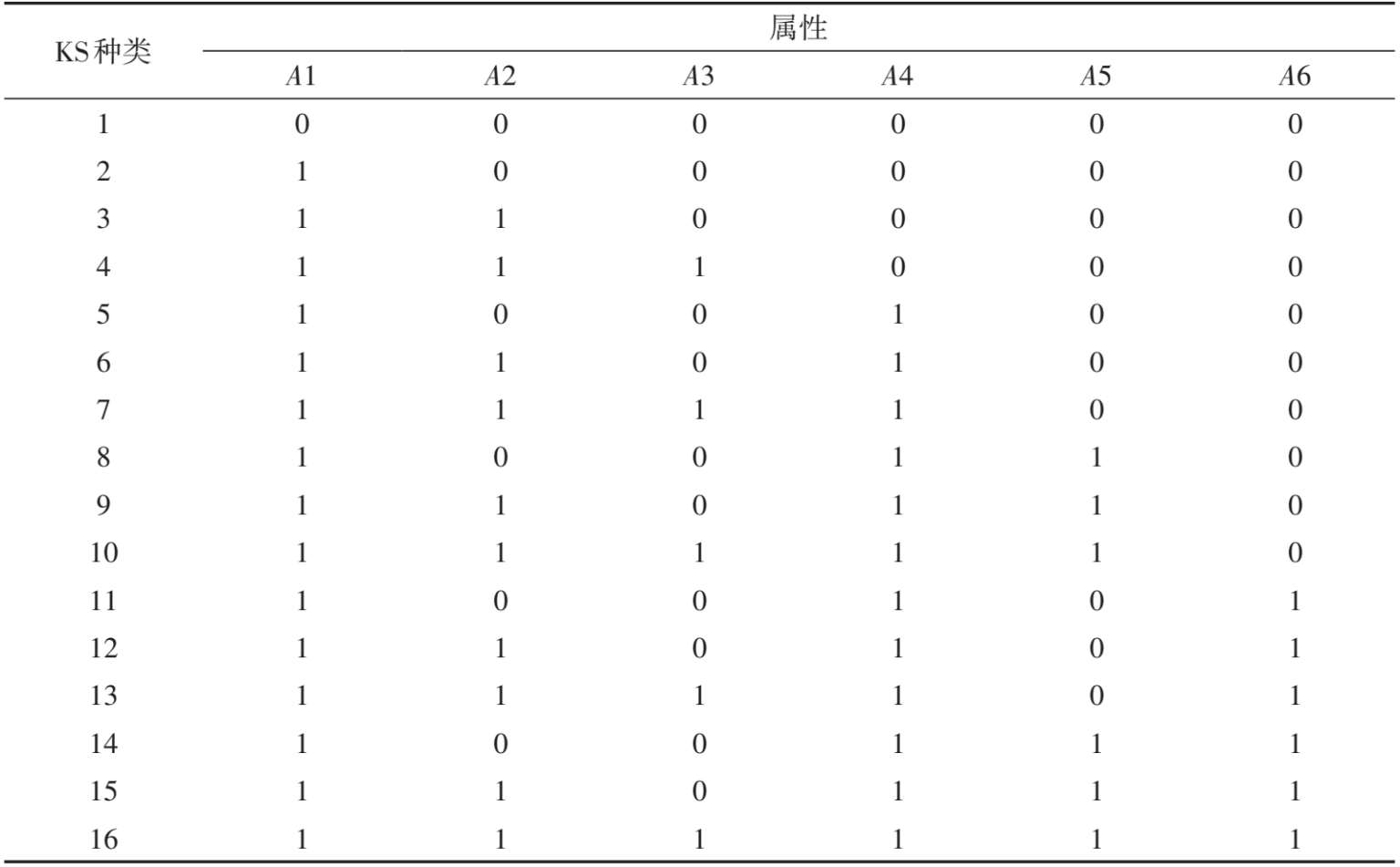
知识状态KS是指属性层级结构下,所有可能出现的知识结构类型。KS最简单的获取方式是将 Qr 阵转置并加上一行0向量(代表一个属性都未掌握情况)。图3.1B下所有可能的知识结构共有 16种,如表 3.3所示。例如,第一行表示 6个所考查的属性均没有掌握的个体,记作α =(0,0,0,0,0,0)。当属性层级结构为独立型时,KS的种类最多,等于 2 K 。可以看出,有了层级的约束,会使得KS数量以及 Qt 阵里的题目类型数量大大减少。
表3.3 图3.1B结构下的KS种类