




点的运动轨迹构成了线,两点可以确定一条直线。直线在某一投影面上的投影是通过该直线上各点的投影线所形成的平面与该投影面的交线,故直线的投影一般情况下仍是直线。
按照直线与 3 个投影面的相对位置不同,直线可分为倾斜、平行和垂直 3 种情况。倾斜于投影面的直线称为一般位置直线,简称一般直线,如图 2.17(a)中直线AB;平行或垂直于投影面的直线称为特殊位置直线,简称特殊直线。如图 2.17(a)中,直线CD为投影面平行线,直线EF为投影面垂直线。
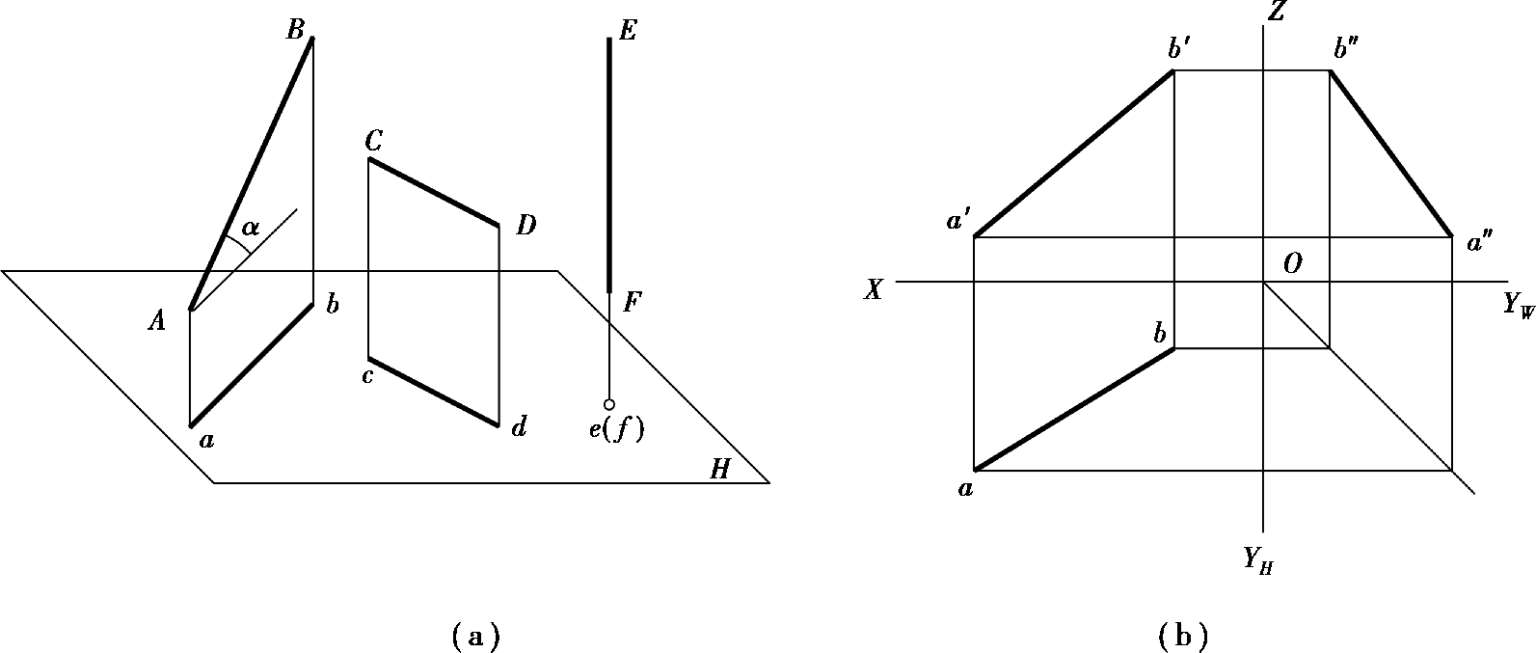
图2.17 直线的投影
作某一直线的投影,只要作出属于直线的任意两点的三面投影,然后将两点的同面投影相连,即得直线的三面投影。图 2.17(b)中,只要作出属于直线的点A(a,a′,a″)和点B(b,b′,b″),将ab,a′b′,a″b″连成直线,即为直线AB的三面投影。
直线与投影面之间的夹角,称为直线的倾角。我们约定直线与H、V、W面的夹角分别用α、β、γ来表示。直线的投影特性反映为:
①当直线AB倾斜于投影面时,其投影小于实长(如ab = AB cos α)。
②当直线CD平行于投影面时,其投影与直线本身平行且等长(如cd = CD)。
③当直线EF垂直于投影面时,其投影积聚为一点。
因此,直线的投影一般仍为直线,只有当直线垂直于投影面时,其投影才积聚为一点。以上直线的各投影特性对于投影面V和W也具有同样的性质。
平行于某一投影面且倾斜于另外两个投影面的直线,称为投影面平行线。按照直线平行于不同的投影面,可分为以下 3 种:
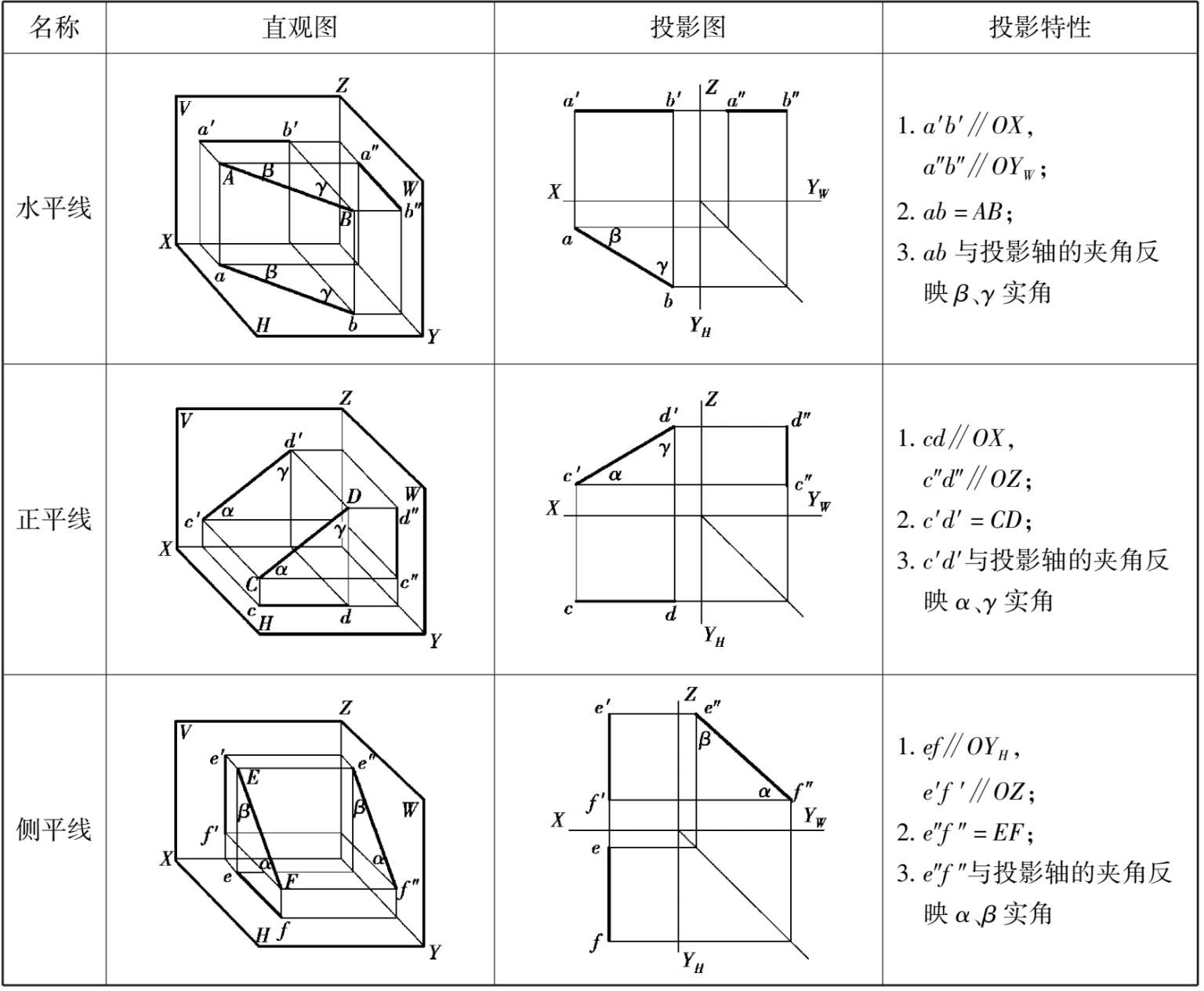
平行于H面且倾斜于V、W面的直线称为水平线,如表 2.2 中直线AB。
平行于V面且倾斜于H、W面的直线称为正平线,如表 2.2 中直线CD。
平行于W面且倾斜于H、V面的直线称为侧平线,如表 2.2 中直线EF。
它们的直观图、投影图和投影特性见表 2.2。
以水平线AB为例,其投影特征如下:
由于直线AB平行于H面,同时又倾斜于V、W面,其H面投影ab与直线AB平行且相等,即ab反映直线的实长,ab = AB。H面投影ab倾斜于OX轴、OY H 轴,其与OX轴的夹角反映直线AB对V面的倾角β的实形,和OY H 轴的夹角反映直线AB对W面的倾角γ的实形。直线AB的V面投影a′b′和W面投影a″b″分别平行于OX轴和OY W 轴,且同时垂直于OZ轴。
同理,可分析出正平线CD和侧平线EF的投影特征。
综合表 2.2 中水平线AB、正平线CD、侧平线EF的投影规律,可以归纳出投影面平行线的投影特性如下:
①投影面平行线在其所平行的投影面上的投影反映实长,且倾斜于投影轴。该投影与相应投影轴之间的夹角反映空间直线对另两个投影面的倾角。
②其余两个投影分别平行于相应的投影轴,这两条投影轴正好组成空间直线所平行的投影面。
表2.2 投影面平行线
垂直于一个投影面的直线,称为投影面垂直线。按照垂直于不同的投影面来分类,直线可分为以下 3 种:
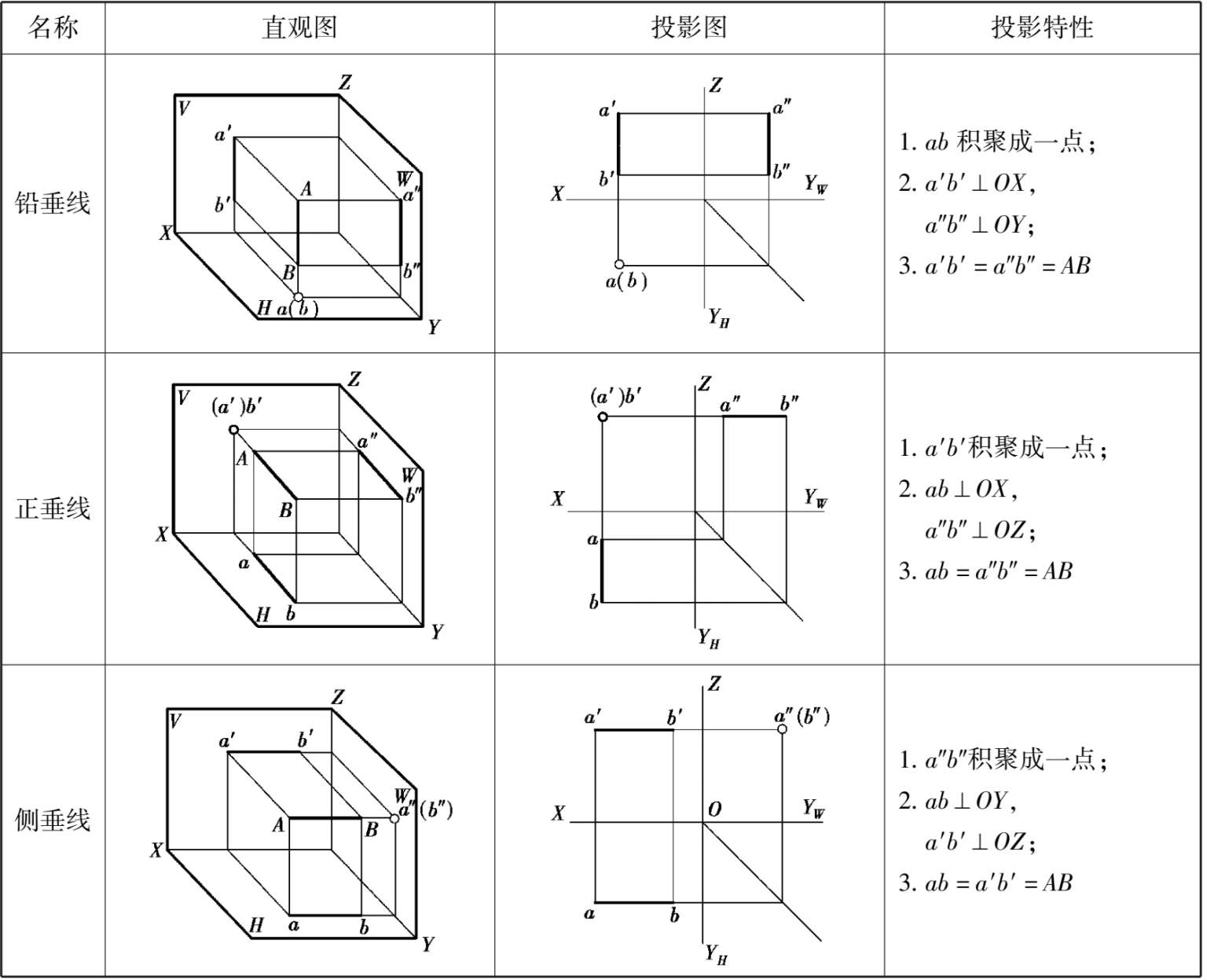
垂直于H面的直线称为铅垂线,如表 2.3 中直线AB。
垂直于V面的直线称为正垂线,如表 2.3 中直线CD。
垂直于W面的直线称为侧垂线,如表 2.3 中直线EF。
它们的直观图、投影图和投影特性见表 2.3。
以铅垂线AB为例,其投影特征如下:
由于直线AB垂直于H面,所以必定平行于V面和W面,其H面投影积聚为一点a(b)。V面投影a′b′垂直于OX轴,W面投影a″b″垂直于OY W 轴,且同时平行于OZ轴。V面投影a′b′和W面投影a″b″均反映空间直线AB实长。
同理,可分析出正垂线CD和侧垂线EF的投影特征。
综合表 2.3 中铅垂线AB、正垂线CD、侧垂线EF的投影规律,可以归纳出投影面垂直线的投影特性如下:
①直线在其所垂直的投影面上的投影积聚为一点。
②直线的另外两个投影垂直于相应的投影轴,这两条投影轴正好组成空间直线所垂直的投影面,且两投影均反映直线的实长。
表2.3 投影面垂直线
与H、V、W三个投影面均倾斜(即不平行又不垂直)的直线称为一般位置直线,简称一般直线。如图 2.18(a)中,AB就是一般位置直线。AB与H、V、W面的倾角分别为α、β、γ。图2.18(b)表示一般位置直线AB的三面投影图,其投影特性如下:
①一般直线在 3 个投影面上的投影均倾斜于投影轴。
②各投影与投影轴的夹角不能反映直线AB对投影面的真实倾角。
③各投影的长度均小于直线AB的实长,分别有:ab = AB cos α,a′b′ = AB cos β,a″b″ = AB cos γ(α、β、γ的值在 0°~90°范围内)。
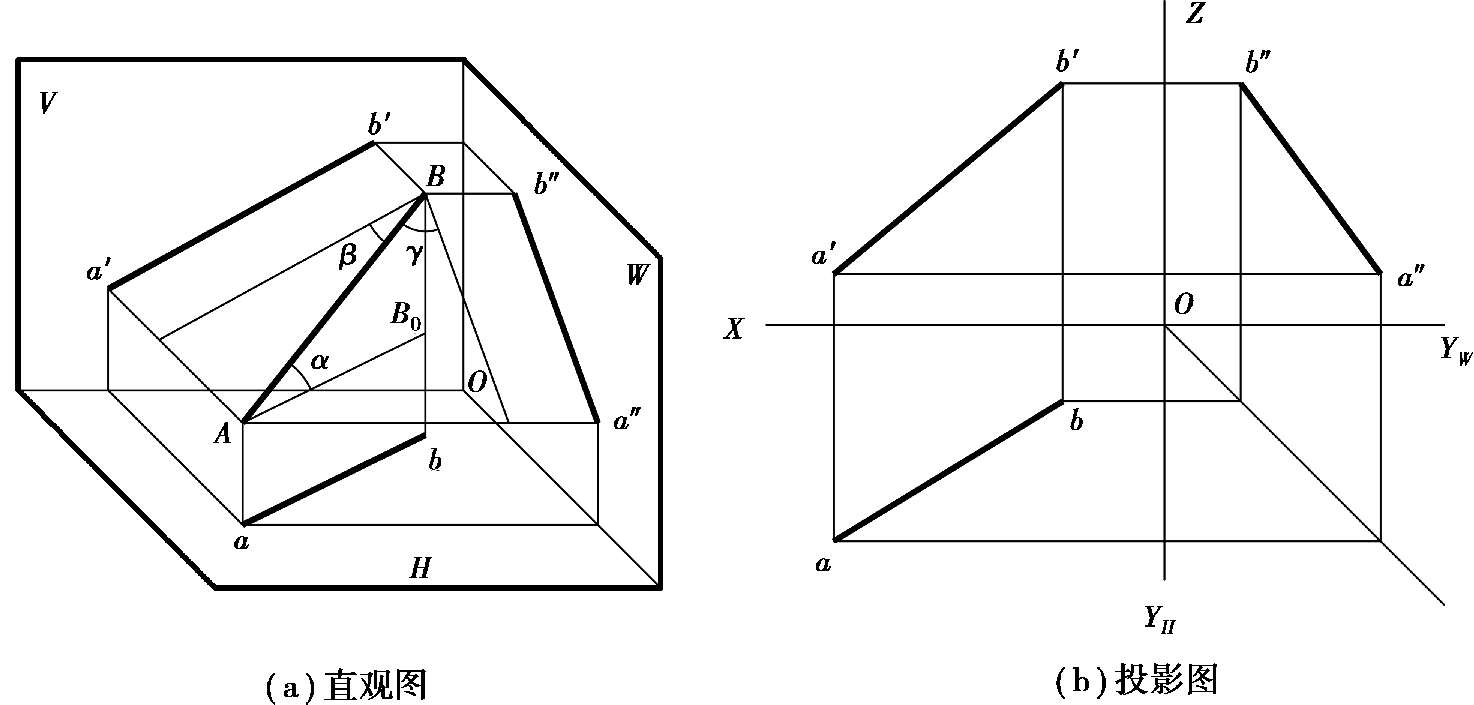
图2.18 一般位置直线
由于一般位置直线对三个投影面的投影都是倾斜的,故 3 个投影均不反映该直线的实长及其对投影面的倾角。但可以根据直线的投影,用图解的方法来进行求解。下面用直角三角形法来解决一般位置直线实长及倾角的求法。

如图 2.19(a)所示,AB为一般位置直线,在AB与其水平投影ab所决定的平面ABba内,过点A作AB 0 ∥ab,与Bb相交于B 0 点。由于Bb⊥ab,所以AB 0 ⊥BB 0 ,△AB 0 B是直角三角形。该直角△AB 0 B中有:斜边AB是实长(用SC来表示实长),∠BAB 0 = α =直线AB对H面的倾角,AB 0 = ab =直线的H面投影长度,B 0 B = Bb - Aa = Z B - Z A (即B、A两点到H面的距离差)。因此,只要作出△AB 0 B,便可求出一般位置直线AB的实长和对H面的倾角α。
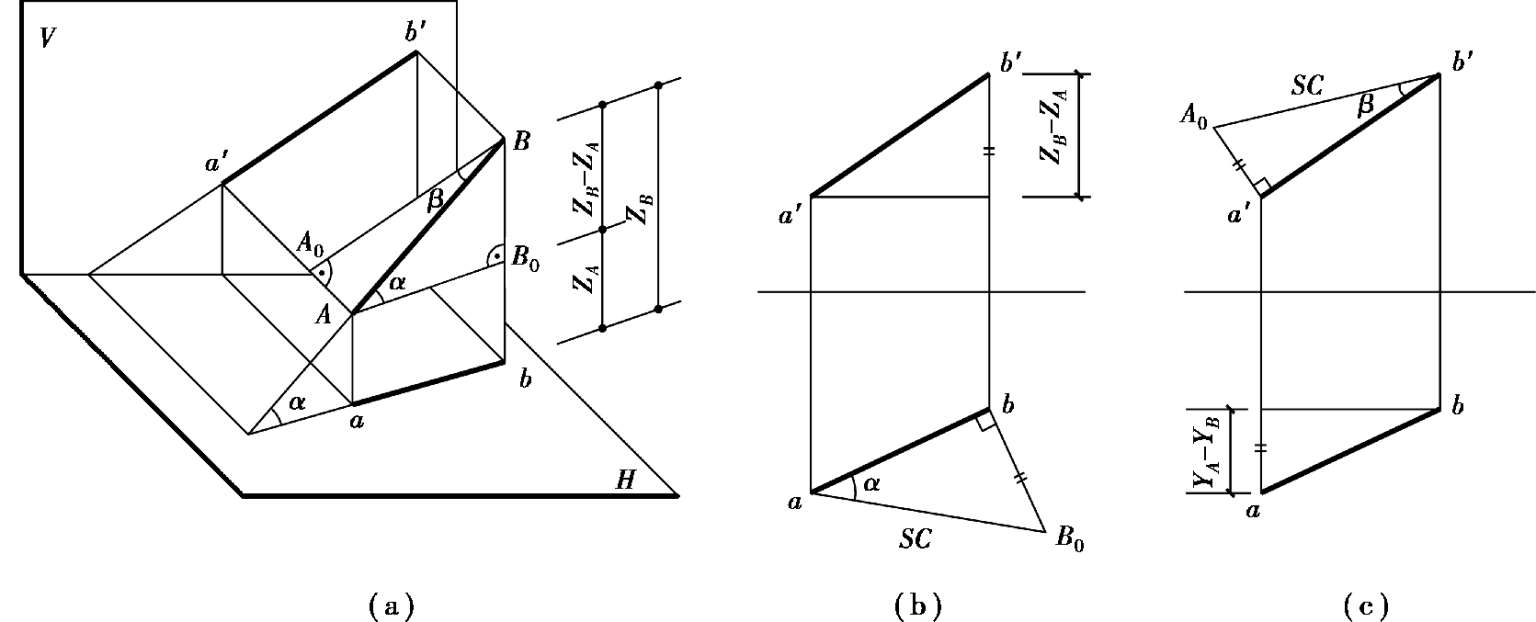
图2.19 求一般位置直线AB的实长及倾角
同理,过点B作BA 0 ∥a′b′,则△AA 0 B也是直角三角形,亦有:斜边仍是空间直线AB,∠ABA 0 = β =直线AB对V面的倾角,BA 0 = a′b′ =直线的V面投影长度,A A 0 = Y A - Y B (即A、B两点到V面的距离差)。因此,只要作出△AA 0 B,便可求出一般位置直线AB的实长和对V面的倾角β。
根据上述方法,在投影图中以水平投影ab为一条直角边,过b(或a)引ab的垂线,并在该垂线上量取bB 0 = Z B - Z A ,连aB 0 即为直线AB的实长,aB 0 与ab的夹角(即bB 0 边所对的角)便是AB对H面的倾角α,如图 2.19(b)所示。
以a′b′为一条直角边,过a′(或b′)作a′b′的垂线,在该垂线上量取a′A 0 = Y A - Y B ,连A 0 b′即为直线AB的实长,A 0 b′与a′b′的夹角便是直线AB对V面的倾角β,如图 2.19(c)所示。
综上所述,在投影图上求直线的实长和倾角的方法是:以直线在某个投影面上的投影为一条直角边,以直线的两端点到该投影面的距离差为另一条直角边作直角三角形,该直角三角形的斜边就是所求直线的实长,而此斜边与投影的夹角,就是该直线对该投影面的倾角。
以上求一般位置直线的实长和倾角的方法,称为直角三角形法。此直角三角形中,包含了实长、距离差、投影和倾角四个参数。四者任知其中二者,即可作出一个直角三角形,从而便可求出其余两个。需要注意的是:距离差、投影、倾角三者是对同一投影面而言。
属于直线的点的投影必在该直线的同面投影上,且符合点的投影规律。
如图 2.20(a)所示,直线AB的H面投影为ab,若点M属于直线AB,则过点M的投射线Mm必属于包含AB向H面所作的投射平面ABba,因此Mm与H面的交点M必属于该投射平面与H面的交线ab。同理,可知m′必属于a′b′。
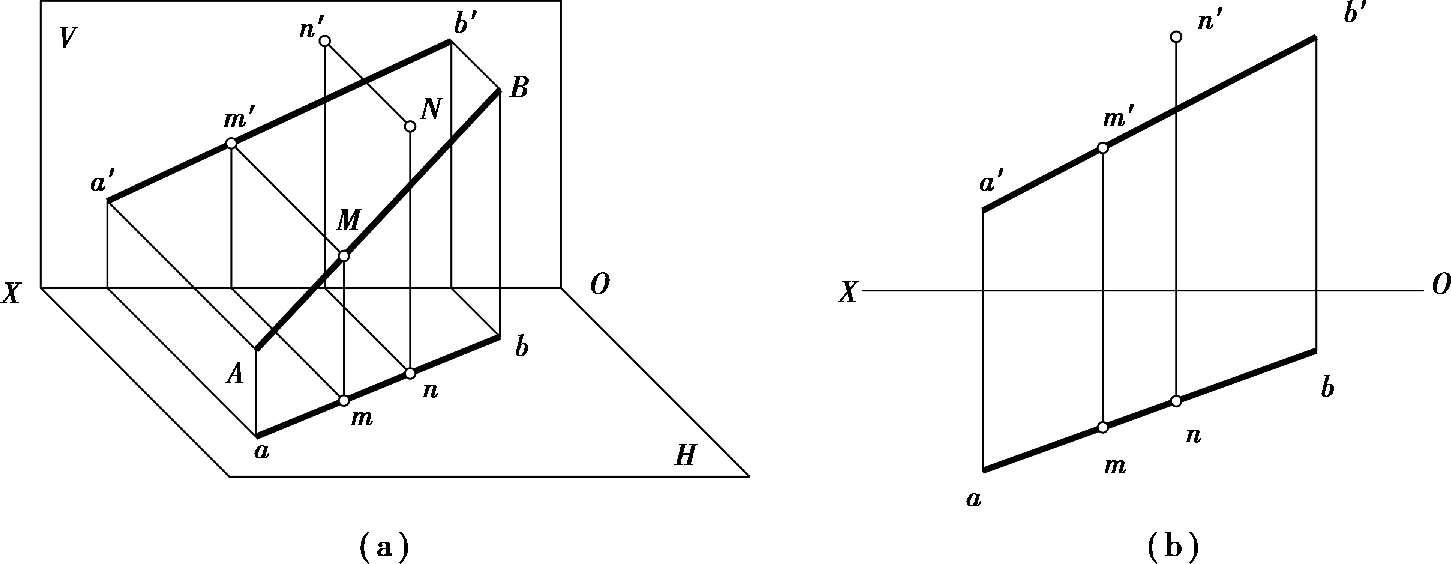
图2.20 属于直线的点的投影
反之,如果点的各个投影均属于直线的各同面投影,且各投影符合点的投影规律,即投影连线垂直于相应的投影轴,则该点属于该直线。如图 2.20(b)中,点M属于直线AB,而点N不属于直线AB。
点分线段成某一比例,则该点的投影也分该线段的投影成相同的比例。
在图 2.20(a)中,点M分空间直线AB为AM和MB两段,其水平投影m也分ab为am和mb两段。在投射平面ABba中,直线AB与ab被一组互相平行的投射线Aa、Mm、Bb所截割,则am:mb = AM:MB。同理可得:a′m′:m′b′ = AM:MB和a″m″:m″b″ = AM:MB。所以,点分直线段成定比,投影后比例不变,即:
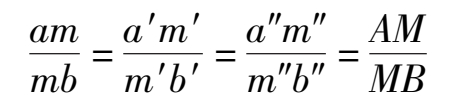
两直线的相对位置有 3 种:平行、相交和相叉(即异面)。
根据平行投影的特性可知:两直线在空间相互平行,则它们的同面投影也相互平行。
对于一般位置的两直线,只需根据任意两面投影互相平行,就可以断定它们在空间也相互平行,如图 2.21 所示。但对于特殊位置直线,有时则需要作出它们的第三面投影,来判断它们在空间的相对位置。如图 2.22 中的两条侧平线AB和CD,虽然V面、H面的投影都平行,但它们的W投影并不平行,所以在空间里这两条侧平线线是不平行的。当然,也可以根据两直线投影中的比例关系来确定他们是否平行,如图 2.22 中的两条侧平线AB和CD的V投影与H投影的比例关系明显不同,故这两条侧平线线是不平行的。
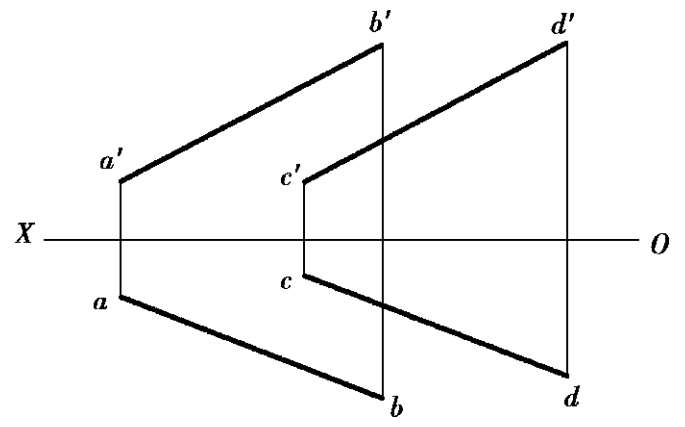
图2.21 两一般位置直线平行
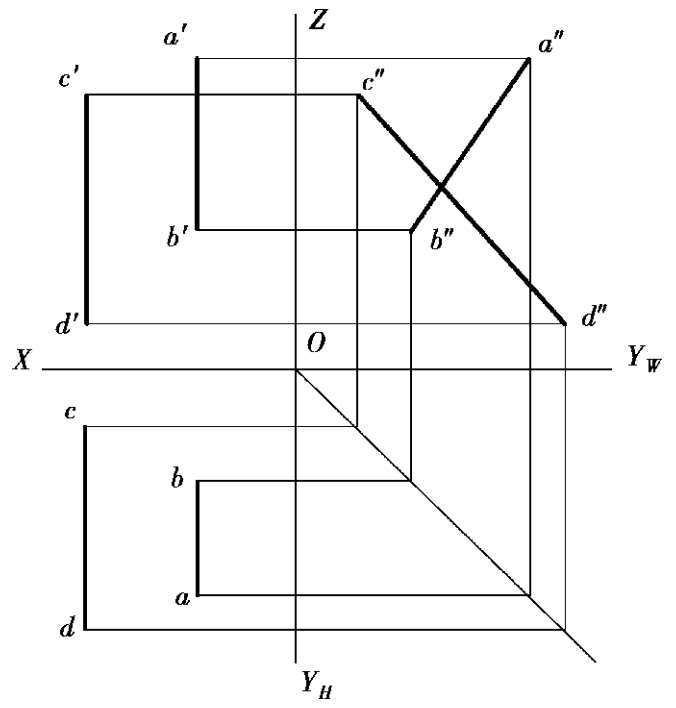
图2.22 不平行的两侧平线
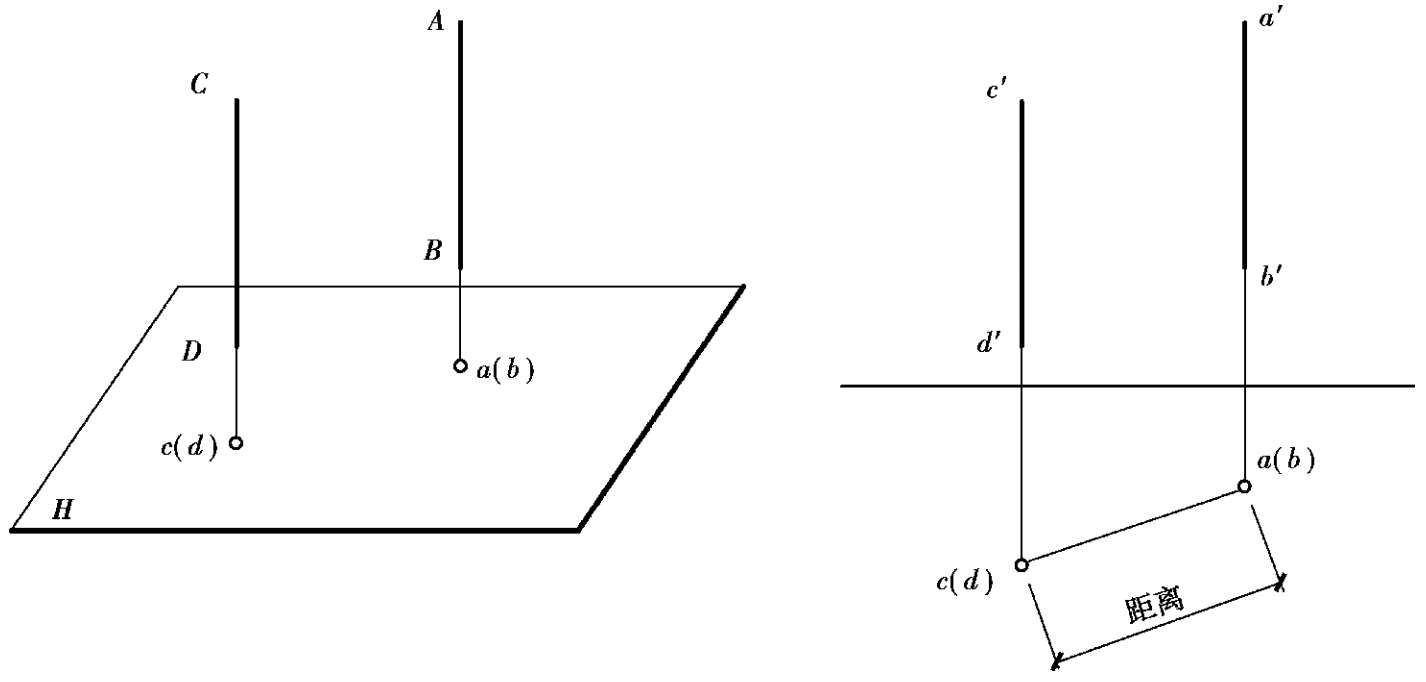
图2.23 两平行线垂直于同一投影面
如果相互平行的两直线都垂直于同一投影面,如图 2.23 所示,则在该投影面上的投影都积聚为两点,且两点之间的距离反映出两条平行线的真实距离。
所有的相交问题都是一个共有的问题,因此,两相交直线必有一个公共点,即交点。由此可知:两相交直线,则它们的同面投影也相交,而且交点符合点的投影特性。
同平行的两直线一样,对于一般位置的两直线,只要根据两面投影,就可以判别两直线是否相交。如图 2.24 所示的直线AB和CD是相交的;而图 2.25 中的直线AB和CD就不相交,它们是交叉的两直线。但是,当两直线中的一条是投影面的平行线时,有时就需要看一看它们的第三面投影或通过直线上点的定比性来判断。
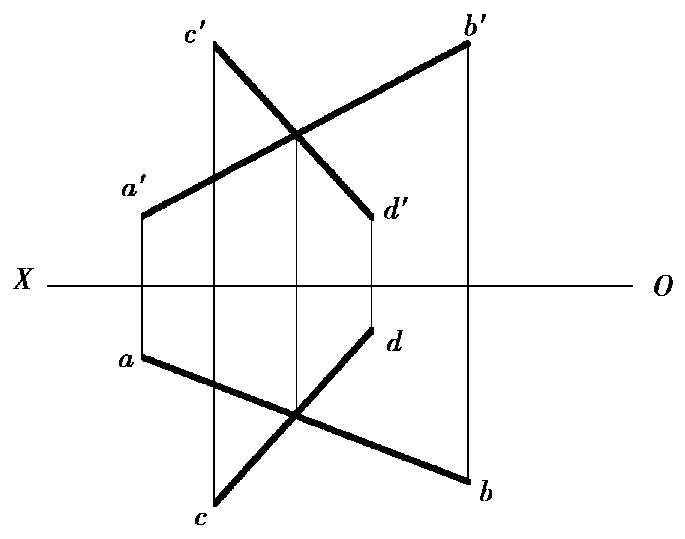
图2.24 相交的两直线图
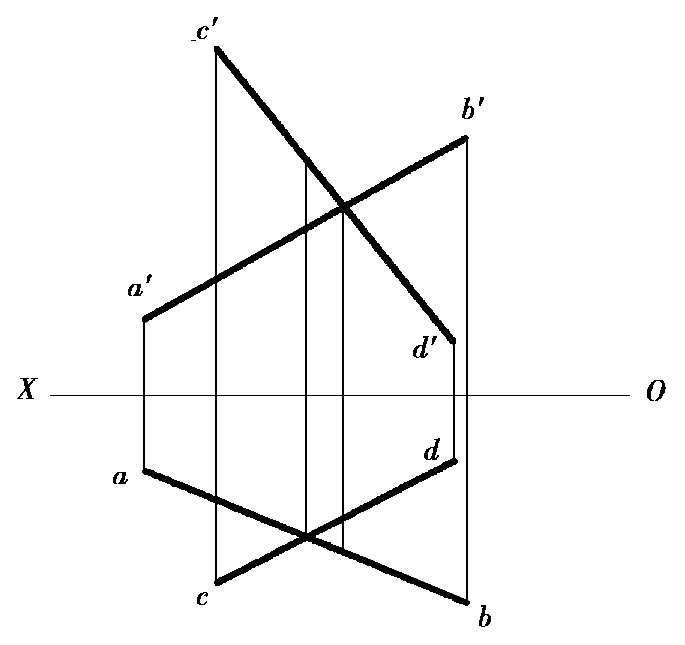
图2.25 交叉的两直线
当两相交直线都平行于某投影面时,相交二直线的夹角等于相交二直线在该投影面上的投影的夹角,如图 2.26 所示。
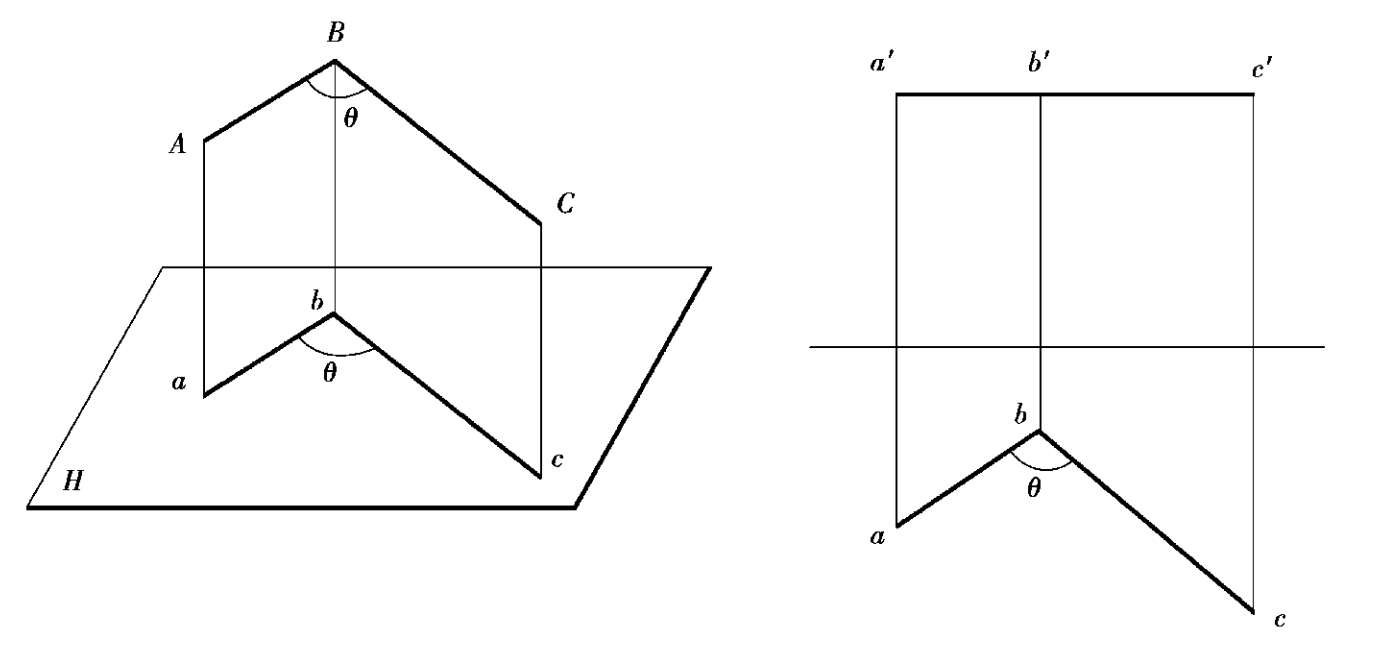
图2.26 平行于投影面的两相交直线该投影面上两直线的反映真实夹角
如图 2.27 所示,在空间里既不平行也不相交的两直线,就是相叉直线。由于交叉直线不能同在一个平面内,在立体几何中把交叉直线又称为异面直线。
如果两条直线的同面投影相交,要判断这两条直线是相交的还是相叉的,就要判断它们的同面投影交点是否符合直线上的点的从属性或定比性。如图 2.27 中,V投影a′b′和c′d′的交点与H投影ab和cd的交点是重影点,则AB与CD为相叉直线。
事实上,交叉两直线投影在同一投影面的交点是这个投影面的重影点。如图 2.27 中,ab和cd的交点是空间AB上的Ⅰ点和CD上的Ⅱ点的H投影。Ⅰ在Ⅱ的正上方,H投影 1 重合于 2,用符号 1(2)表示。同样的,a′b′和c′d′的交点是空间CD上的Ⅲ点和AB上的Ⅳ点的V投影,Ⅲ在Ⅳ处正前方,V投影 3′重合于 4′,用符号 3′(4′)表示。
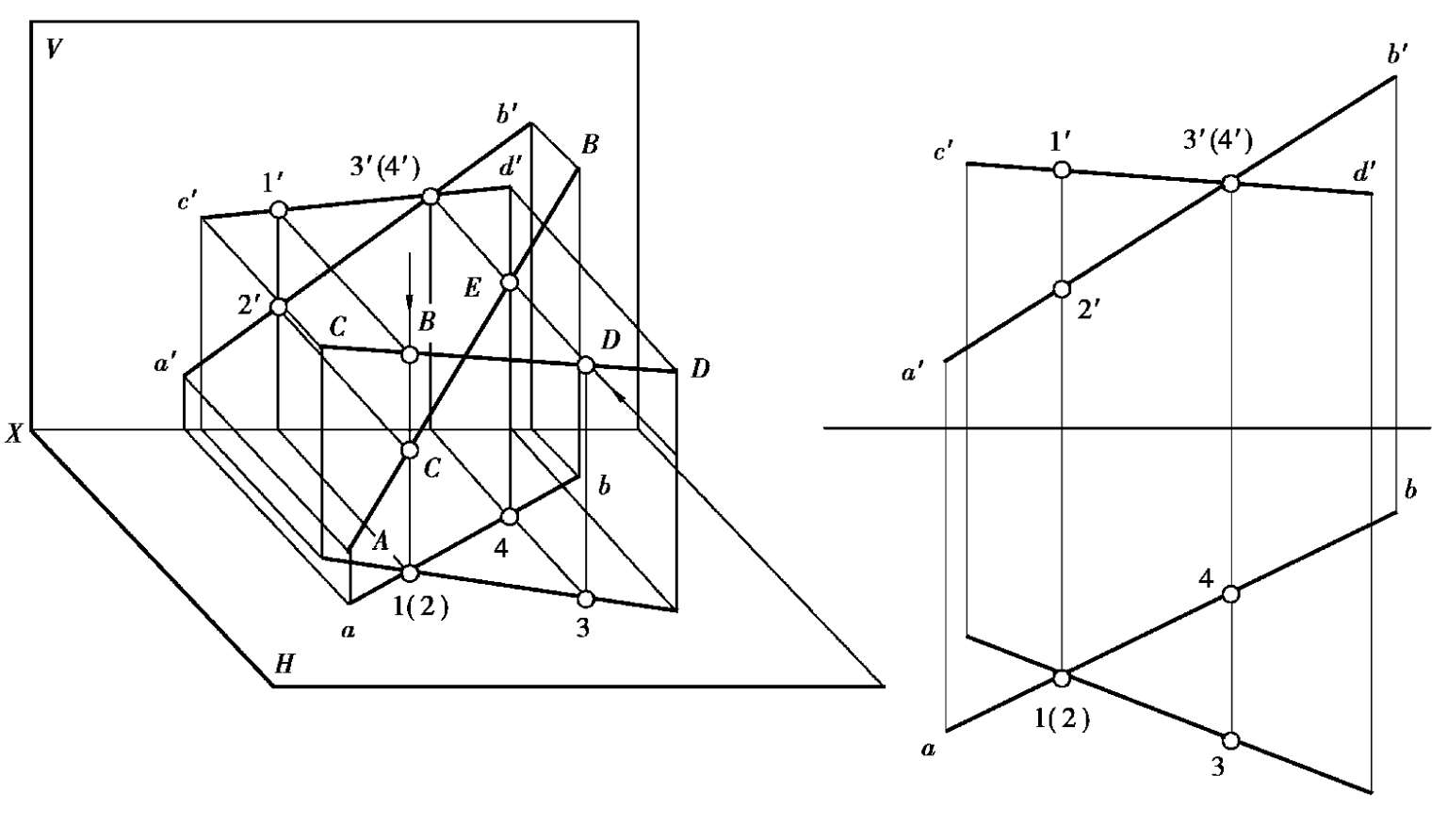
图2.27 交叉直线
如果两条直线中有一条或两条是侧平线,并且已知的是V、H投影,则可通过W投影判断两直线的相对位置是平行还是交叉,如图 2.28 所示。当然也可以利用CD的V、H投影中所谓交点的定比性来判断,如图 2.28 中CD的V、H投影中。如果将 1′、1 视为c′d′及cd上,其定比性显然不同,故直线AB、CD为交叉二直线。
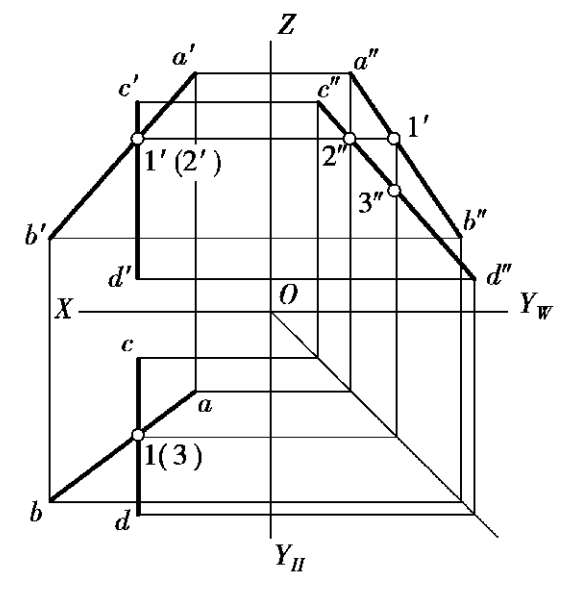
图2.28 交叉直线中有一条侧平线
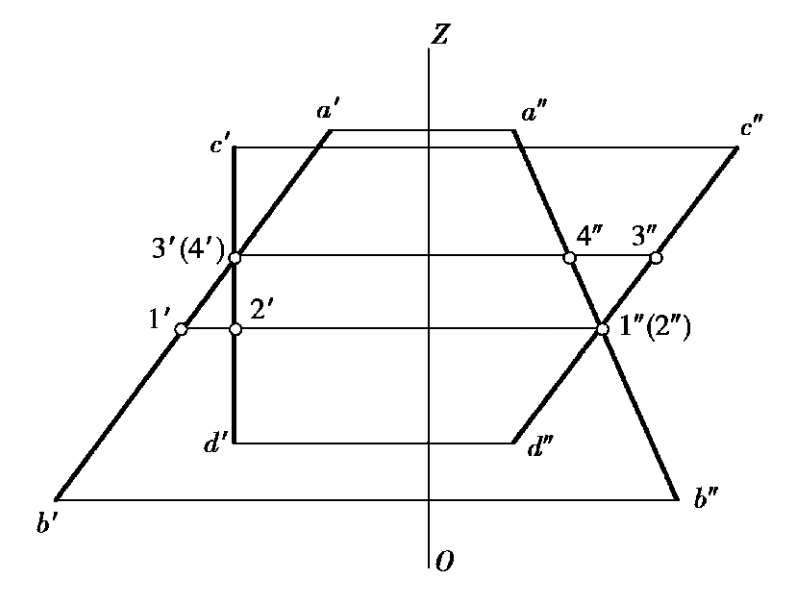
图2.29 判别交叉直线的可见性
【例 2.1】 判别交叉两直线AB和CD上重影点的可见性,如图 2.29 所示。
【解】 ①从W投影的交点 1″(2″)向左作投影连线,与c′d′相交于 2′,与a′b′相交于 1′。因为1′在2′左方,所以AB上的Ⅰ点在CD上的Ⅱ点的正左方。1″可见,2″不可见,在W投影上将 2″打上括号。
②从V投影的交点 3′(4′),向右作投影连线,与a″b″相交于 4″点,与c″d″相交于 3″点。因为 3″在 4″之前,故 3′可见,4′不可见,在V投影上将 4′打上括号。