




温度对反应速率的影响主要是影响反应速率常数。温度升高,吸放氢反应的各步骤(物理吸附、化学吸附、表面渗透、氢扩散、β相长大和界面化学反应)的速率一般都是增大的。不同温度下的速率常数基本符合van’t Hoff规则:当温度升高 10 K时,反应速率增大 2~4 倍,即

式中 k T —— T 温度下的速率常数;
k T +10 —— T +10 温度下的速率常数,单位为K。
根据这个规律,人们可以大致估算温度对吸放氢反应速率的影响。但对于精确分析温度的影响,则需要利用前面的动力学模型计算具体温度下的反应速率常数或特征时间。
计算反应速率常数首先要选择合理的动力学模型,选择的依据是通过不同的动力学模型分别拟合反应分数 ξ- 时间 t 关系,比较拟合数据的相关系数和计算误差,选择相关系数最大、误差项最小的模型,认为是最能描述该吸放氢反应机理的模型形式。通常动力学模型可以表示为 f ( ξ )= kt 的形式,其中 f ( ξ )依据不同的理论模型具有不同的形式,从而可以判断反应的不同控速步骤。以图解法解析时,用 f ( ξ ) -t 作图,斜率即为反应速率常数 k 。而不同温度下的速率常数遵循Arrhenius方程,即

或

式中 E a ——吸放氢反应的表观活化能,J/mol;
R ——气体常数,等于 8.314 J/(mol·K);
T ——反应温度,K;
A ——指前因子。
通过ln k 对 1/ T 作图,即可求出反应的表观活化能。
下面分别以纯Mg、Mg-Er和Mg-LaNi 5 合金举例说明如何计算反应速率常数 k 或者特征时间 t c 。图 2.5(a)和(b)分别为纯Mg和Mg-Er合金粉末的吸氢动力学曲线 [20] 。纯Mg粉末在 573 K时 5 min内可以吸氢 4.2 wt % ,而在 473 K时,2 h内只吸收了 3.1 wt %的氢气,说明吸氢速率在 473 K时很缓慢。而Mg-Er合金粉末在573 K时 5 min内可以吸氢 6.0 wt % ,远高于纯Mg;473 K时,2 h内吸氢 3.67 wt % ,比纯Mg也要高一些。纯Mg粉末特定时间内的吸氢量随温度的升高而增大,Mg-Er合金也是如此,但纯Mg在 473~573 K温度范围内单位时间内的吸氢量都低于Mg-Er合金粉末。为了定量地比较纯Mg在不同温度下的吸氢速率,以及添加Er后不同温度下的吸氢速率变化,就需要通过动力学模型来计算各温度下的具体反应速率常数。
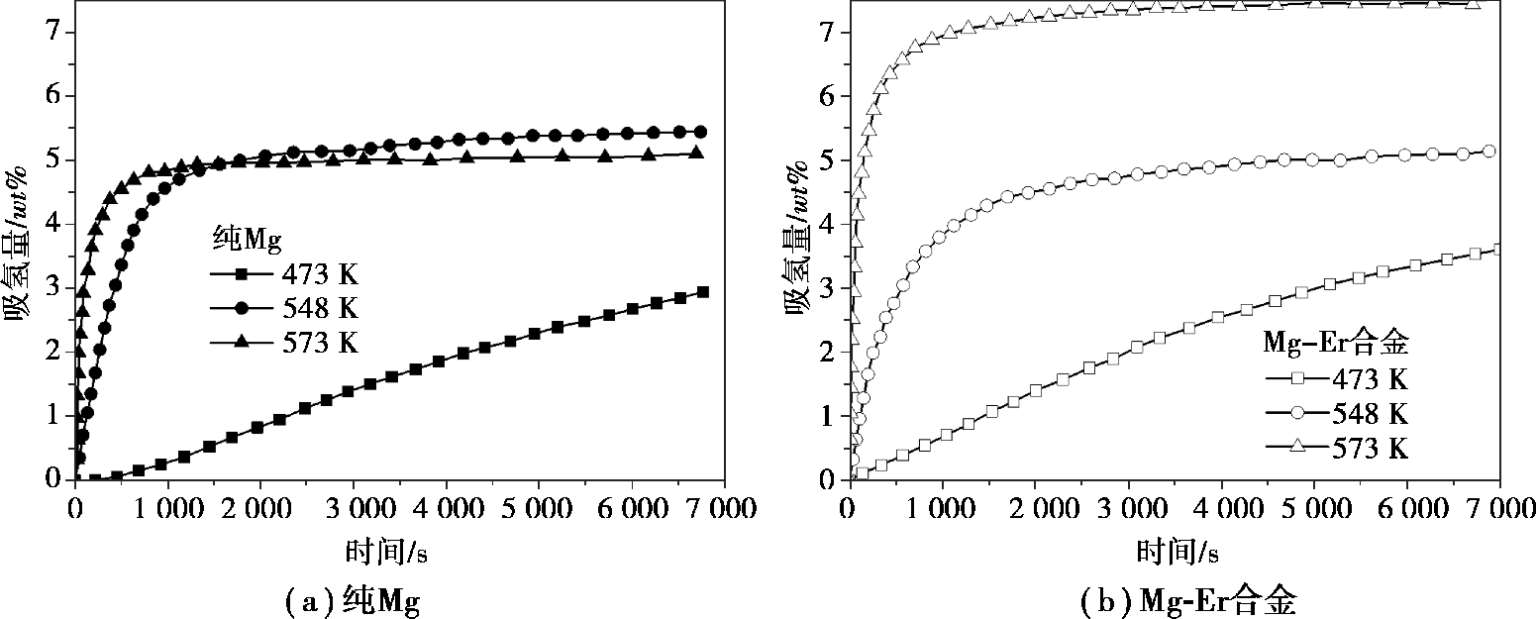
图 2.5 Mg及Mg-Er合金的吸氢动力学曲线 [20]
通过2.2.2 节各动力学模型的计算比较,纯Mg和Mg-Er合金粉末可以被JMAK模型较好地描述。 JMAK模型的函数形式可以转变为
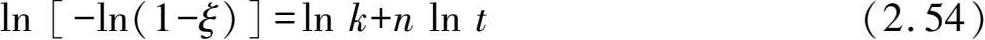
利用ln[-ln(1 - ξ )]对ln t 作图,如图 2.6 (a)和(b)所示,拟合获得的斜率即为Avrami指数,截距为ln k 。随着温度层从 473 K升高至 573 K,纯Mg的Avrami指数从 1.74 降低至 0.6,对应于不同维度的扩散控速,ln k 则从-14.38 增加至-2.99,说明反应速率随温度增加;Mg-Er合金的Avrami指数略小于纯Mg,其ln k 随温度从-9.44 增加至-2.51,皆高于纯Mg的反应速率常数。通过ln k 分别对 1000/ RT 作图,如图 2.6 (c)所示,拟合的直线斜率即为- E a 。纯Mg吸氢的表观活化能为243.92 kJ/mol H 2 ,而Mg-Er合金的表观活化能仅为 143.48 kJ/mol H 2 ,远低于纯Mg,说明合金元素有效降低了反应能垒。
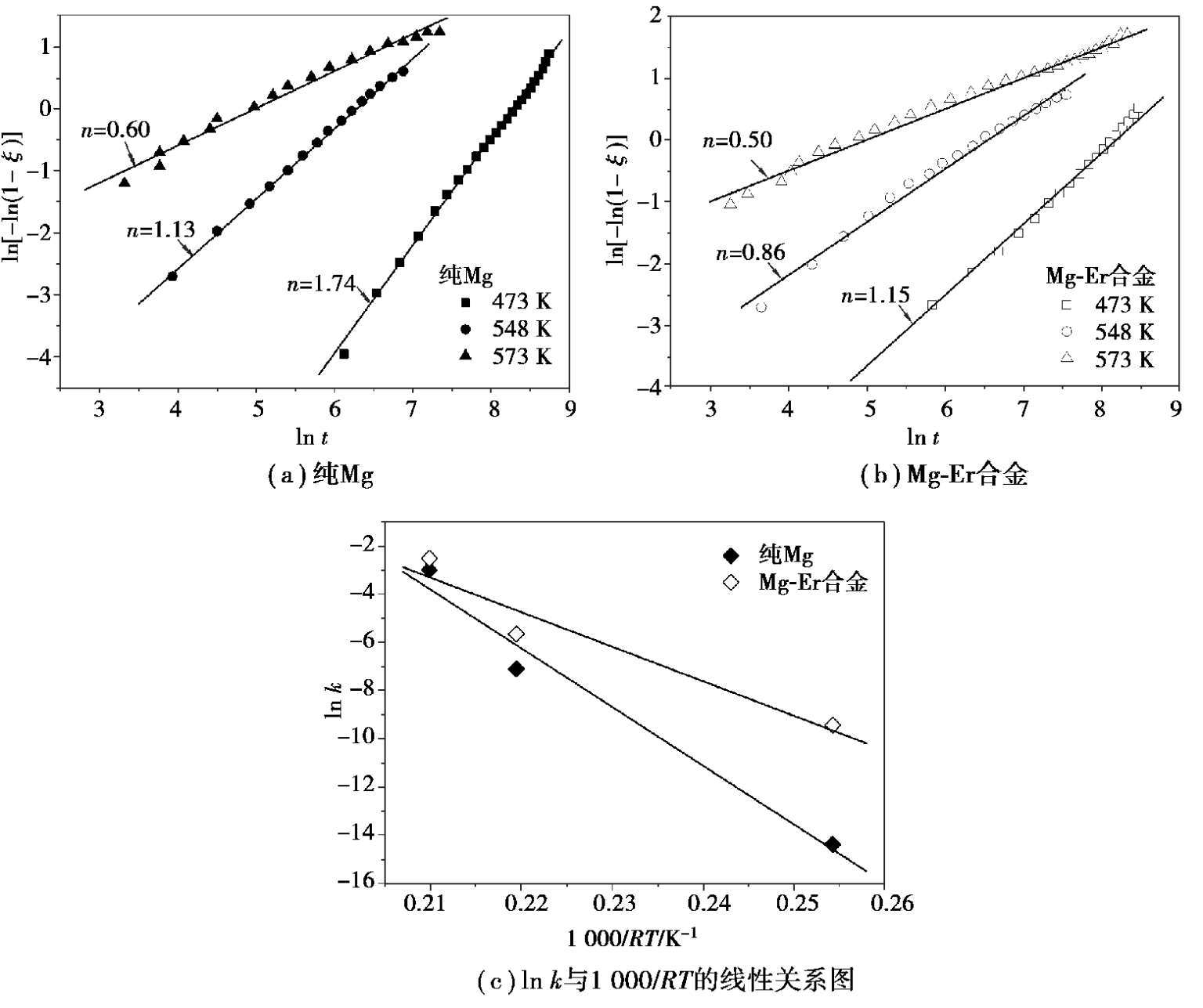
图 2.6 ln[-ln(1- ξ )]与ln t 的线性关系图
以Mg-LaNi 5 合金在不同温度下的吸氢动力学为例说明温度对多相镁合金吸氢的影响。图 2.7 所示为Mg-30 wt % LaNi 5 合金复合物在 473~573 K范围内的吸氢反应分数 ξ 与时间关系 [21] 。 Mg-30 wt % LaNi 5 合金包含多种物相,分别为Mg、Mg 2 Ni和Mg 12 La。随着温度的升高,混合物单位时间内能达到的表观反应分数逐渐增加,说明反应速率逐渐加快。为了定量比较各温度下的反应速率,利用各个模型拟合反应动力学数据。除了前面介绍的通过 f ( ξ ) -t 线性关系来计算外,还可以利用计算软件直接拟合 ξ-f ( t )关系。对比各模型的计算结果显示,Chou模型的扩散控速方程可以较好地表述该实验结果,不同温度下的反应分数和时间符合以下方程:

对应的拟合相关系数 r 2 分别为 0.9853(473 K)、0.9985(498 K)、0.9917(523 K)、0.9945(548 K)和 0.9905(573 K),而且计算误差均小于 4.0%。随着温度的升高,特征时间 t c 从 473 K时的 4914 s降低至 573 K的 1564 s。因为特征时间表示反应完全所需的时间,所以计算结果说明了范围速率随着温度的升高而升高。
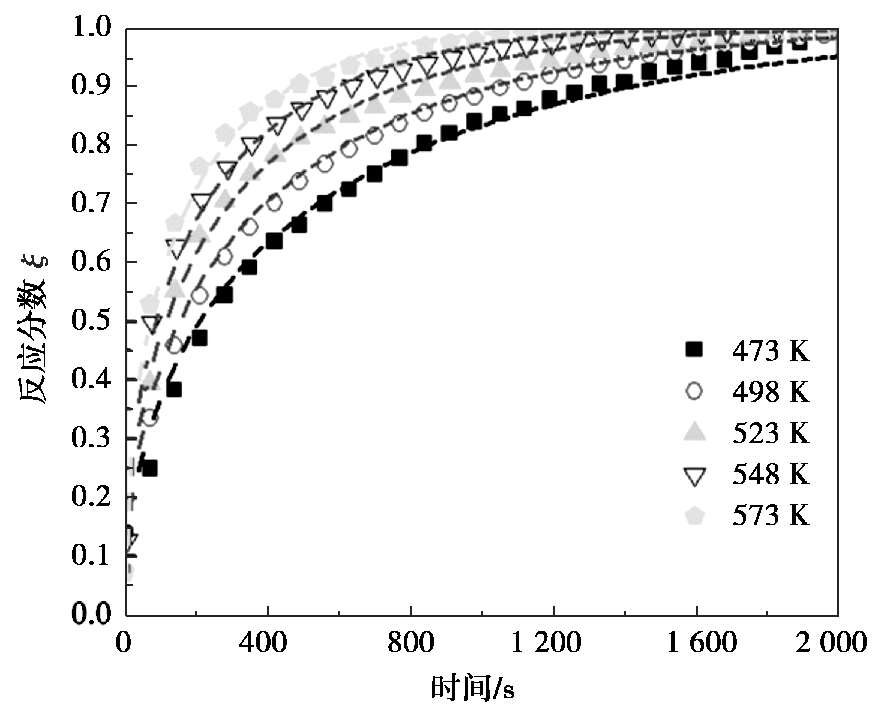
图 2.7 Mg-30 wt % LaNi 5 合金复合物在 473~573 K范围内的吸氢反应分数 ξ 与时间关系 [21]
值得一提的是,当采用Chou模型直接拟合不同温度下的实验数据时,由于Chou模型解析了扩散系数或化学反应速率常数与温度之间的关系,将Arrhenius方程已经内化在Chou模型中,所以可以根据式(2.56)
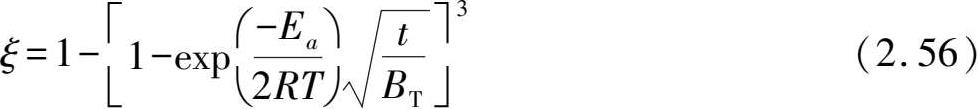
进一步计算出反应的活化能。式(2.56)由式(2.26)变换而来,其中假设
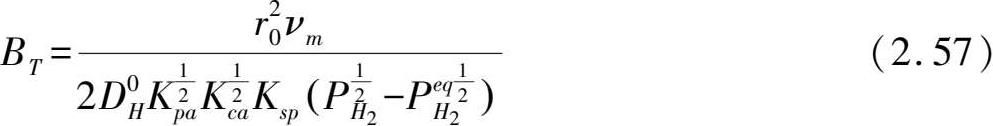
对于特定材料和既定反应条件下为一常数值。此外,通过任意两个温度下计算的活化能和方程系数 B T ,就可以预测其他温度下的反应动力学曲线。例如,通过计算473 K和573 K下的反应表观活化能为(25.2±0.1)kJ/mol H 2 ,以及 B T 为8.25,则其他温度下的反应分数-时间关系
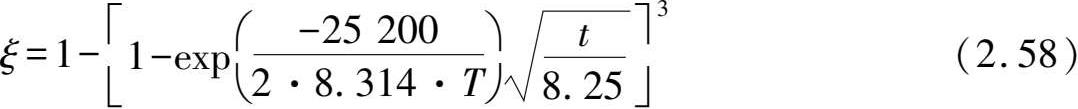
图 2.7 中给出了通过Chou模型预测的反应分数曲线与实验数据的对比,预测结果合理地反映了实验结果,预测误差仅为 1.5%(498 K)、2.4%(523 K)和 1.2%(548 K),表明预测模型的准确性。
从吸放氢反应的Gibbs自由能表达式可以看出,给定氢压与平衡氢压的压差是吸氢和放氢反应的驱动力,而对于动力学过程,氢压差的增加意味着氢气浓度差的增加,也将提高吸放氢反应速率。从表 2.3 可以看到,Chou模型中给出了反应分数与氢压的关系,而其他模型还没有显化压力因素的影响。当固定温度等其他因素,只改变氢压时,扩散为控速环节的粉末颗粒样品反应分数表达式
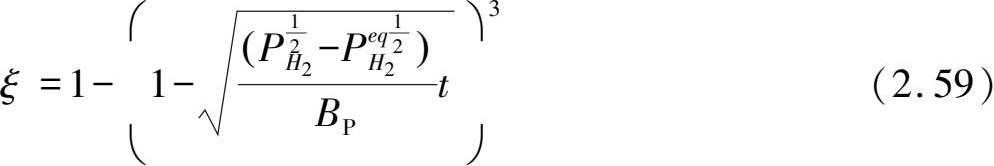
化学反应为控速环节的反应分数表达式
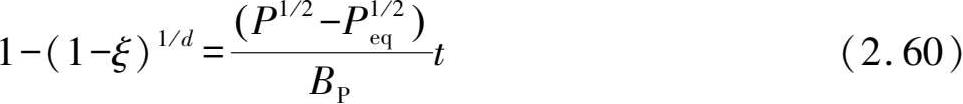
其中
B
p
为与温度相关,而与压力无关的常数。图 2.8 所示为Mg
2
Ni合金在 0.275~1.133 MPa氢压下的吸氢动力学曲线,随着氢压的增大,单位时间内反应分数越大,说明氢压升高增大了反应速率。通过扩散控速的Chou模型可以计算不同氢压下的反应特征时间,分别对应于 3650 s (0.275 MPa)、2452 s(0.512 MPa)、1762 s(0.745 MPa)和 895 s(1.133 MPa)。特征时间随着氢压增大而显著减小,说明反应速率随氢压增大。值得注意的是,利用式(2.59)或式(2.60)来拟合任意两个氢压下的动力学曲线,就可以获得平衡氢压
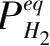 和
B
P
参数。那么,其他氢压条件下的动力学曲线就利用已知的方程进行预测。图 2.8 中Mg
2
Ni的吸氢曲线可以通过式(2.59)进行拟合,获得的
和
B
P
参数。那么,其他氢压条件下的动力学曲线就利用已知的方程进行预测。图 2.8 中Mg
2
Ni的吸氢曲线可以通过式(2.59)进行拟合,获得的
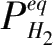 =0.09511 MPa,
B
P
=852.07,则其他氢压下的反应分数
=0.09511 MPa,
B
P
=852.07,则其他氢压下的反应分数
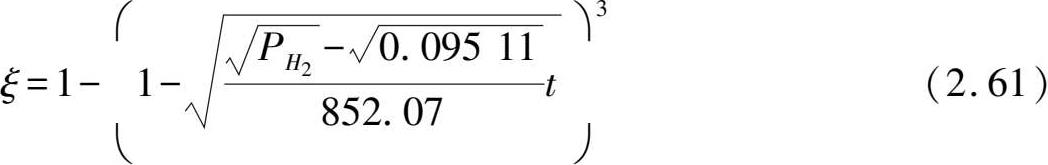
预测曲线与实验点吻合比较好。
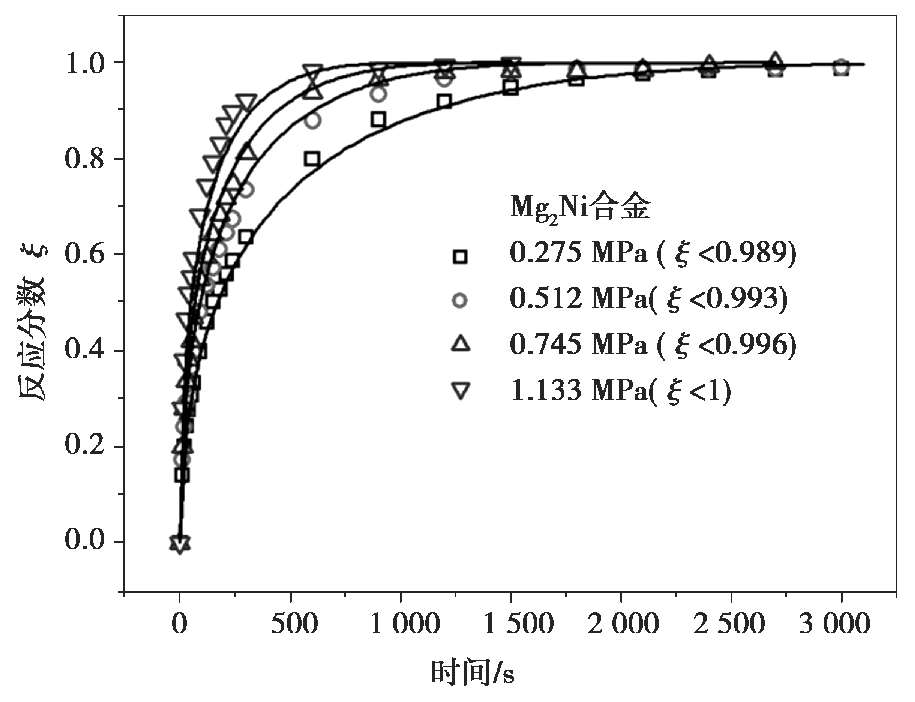
图 2.8 Mg 2 Ni合金在不同氢压下的吸氢动力学曲线
在温度、压力等条件不变的情况下,随着粒径的减小,比表面积增加,扩散距离减小,反应截面增加,吸放氢反应速率一般会加快。2.2.2 节的动力学模型中都给出了反应分数与粒径的关系。对于物理吸附、化学吸附、表面渗透、界面化学反应等过程控速的模型,反应分数与 1/
r
0
成正比;对于氢扩散过程,反应分数与
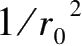 成正比,而对于形核长大过程,粒径的影响没有明确关系,需要结合实验结果详细判断。实际的粉末粒径通常是呈一定分布规律的,通过模型计算给出的粒径应为样品的平均粒径或有效粒径尺寸。
成正比,而对于形核长大过程,粒径的影响没有明确关系,需要结合实验结果详细判断。实际的粉末粒径通常是呈一定分布规律的,通过模型计算给出的粒径应为样品的平均粒径或有效粒径尺寸。
纳米化是提高镁基储氢合金吸放氢速率的有效手段。纳米结构提高了各种缺陷的密度,包括晶界/相界、位错和堆垛层错等,增加了Mg与氢气的接触面积,降低了氢原子在颗粒中和晶界中的扩散距离,有利于储氢合金的吸放氢动力学 [22] 。此外,随着纳米颗粒中含氢量的增加,氢化物的形式能垒降低,从而降低了镁基储氢材料中氢化/脱氢反应的表观活化能。球磨是最常用制备纳米储氢材料的方式,通过球磨制备的Mg 50 Co 50 合金颗粒尺寸为 1~2 μm,而晶粒尺寸仅有几个纳米 [23-25] 。这种Mg 50 Co 50 合金具有Bcc结构,并且展现出较常规Mg-Co合金更高的容量和更快的吸放氢速率。
Ti复合的MgH 2 纳米晶完全放氢后制备出Ti复合的Mg纳米晶,即使在低温下也展现比常规Mg颗粒具有更快的吸氢速率 [25] 。如图 2.9 所示,Ti催化的MgH 2 纳米晶完全放氢后,在 530 K时 1 h内就可以吸 6 wt %氢气,而常规MgH 2 颗粒吸入同样多的氢气量则需要 3 h,并且在 623 K高温。对于纳米化的Mg样品,吸氢更加柔性化,吸氢温度降低至 426 K时,18 h后仍可以存储 5.2 wt %氢气。 Jander模型可以很好地拟合Ti催化的MgH 2 纳米晶和常规MgH 2 颗粒样品的吸氢动力学曲线,说明三维氢原子的扩散是该反应的控速环节。计算得到Ti催化的MgH 2 纳米晶在573 K时的速率常数 k 为 3.06 s -1 ,相当于同温度下常规MgH 2 颗粒样品速率的 40 倍。图2.9 中的小图给出了Jander模型拟合的反应分数函数与时间的线性关系。
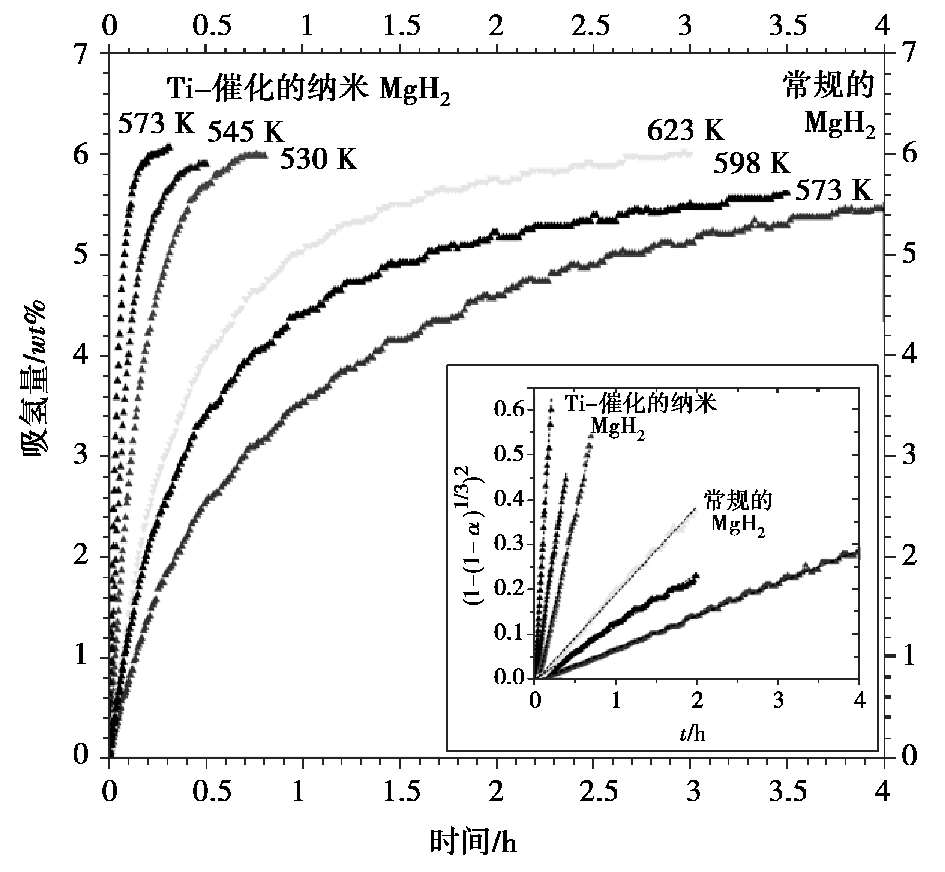
图 2.9 Ti催化的MgH 2 纳米晶样品和常规MgH 2 样品在 1 MPa氢压下的吸氢动力学曲线
除了减小颗粒尺寸外,镁基材料与催化剂复合也会强化镁合金的吸放氢动力学性能。目前已有大量关于镁基储氢合金添加催化剂的研究,包括的催化剂种类有金属氧化物、过渡金属元素、稀土元素、氟化物、卤化物等。催化剂改善动力学性能的机理通常有 4 种,氢泵效应、溢流效应、通道效应和电子转移。氢泵效应是指掺杂的过渡金属在吸放氢过程中会与氢原子形成氢化物,氢优先通过掺杂相形成的氢化物放出,从而削弱氢化物的稳定性,改善放氢动力学性能。溢流效应是指氢气优先在催化剂表面化学吸附并解离,然后氢原子从催化剂表面转移到反应物表面,促进反应进行。通道效应是指催化剂在吸放氢过程中充当氢原子快速扩散的通道,可以促进氢原子的迁移。电子转移是指具有变价的催化剂通过得失电子来促进氢气的化学吸附和脱附过程,从而改善氢化物的形成和分解。催化剂的添加不改变镁合金吸放氢反应的热力学性质,如储氢容量和吸放氢焓变,但是却可以显著降低反应的表观活化能。
金属氧化物是常用的镁基储氢合金催化剂。 Nb 2 O 5 掺杂的MgH 2 样品完全放氢后,在 60 s内可以吸 6.9 wt %氢,并且在 140 s内可以将这些氢完全释放,放氢速率达到 0.011 wt %/s [26] ,这是其他氧化物掺杂无法达到的效果。多价态金属和氢分子发生电子交换,加速了气—固相反应过程是其催化作用的主要原因。5 wt % CeO 2 掺杂的MgH 2 也展现了比新鲜MgH 2 更快的氢化速率。刚制备的MgH 2 在 593 K下 5 min内可以吸氢 3.46 wt % ,而MgH 2 +5 wt % CeO 2 在相同条件下吸氢量可以达到 3.95 wt % [27] 。并且,593 K下 30 min可释放 3.6 wt %氢气,远高于纯MgH 2 的 1.0 wt % 。近些年,过渡金属硫化物如MoS、FeS等对MgH 2 的催化效果也有报道。 MgH 2 -5MoS 2 复合物在 532 K就可以开始放氢,并且在 553 K下 20 min内可以释放 4.0 wt %的氢气 [28] 。
对于过渡金属如Ni、Nb、Ti、Fe和稀土元素La、Ce、Pr、Nd、Sm等的添加研究工作很多。过渡金属Ti和Ni对提高MgH 2 的动力学性能、降低放氢温度和活化能有显著效果。 Mg-TM(Ti,Fe,Ni)-La三元细颗粒粉末具有优异的吸氢动力学行为,且放氢温度要低于二元的Mg-TM和Mg-RE复合物 [20,28-31] 。 NbH x 无序结构纳米颗粒可以显著提升MgH 2 的吸放氢动力学,其在 573 K下 9 min内可以放出 7.0 wt %的氢,并且在 373 K下以可接受的速率吸氢 4.0 wt % 。多元Mg-TM-RE合金通常包含多种物相,如铸态的Mg 80 Ce 18 Ni 2 合金含有 57 wt % CeMg 3 、29 wt % Ce 2 Mg 17 、7 wt %CeMg和 5 wt % CeMgNi 4 [ 32 ,33] 。由于Ni元素、REH x 通常被认为是活性质点,对吸放氢可以起到催化作用,所以活性组元在储氢合金中的均匀分布将有更有效的催化效果。通过原位氢化Mg-Ni-RE金属间化合物获得纳米级复合的REH 2 -Mg-Mg 2 Ni材料展现了优异的吸放氢动力学性能和循环稳定性 [34,35] 。 Nd 4 Mg 80 Ni 8 合金为单相的金属间化合物,由于Nd原子与氢原子的亲和力强,首先生成大量的纳米级NdH 2 颗粒弥散分布于镁合金基体中,使得Nd 4 Mg 80 Ni 8 分解为NdH 2 、α-Mg和Mg 2 Ni。均质的NdH 2 -Mg-Mg 2 Ni纳米复合物不仅热力学上具有较高的储氢容量,细小的组织也使其获得了优异的吸放氢动力学,如图 2.10 所示。利用扩散控速的Chou模型计算吸氢反应的特征时间, t c 从 373 K时的153.5 min降至573 K时的1.6 min,说明反应速率急剧增加。计算的吸氢反应活化能为82.3 kJ/mol H 2 也远低于纯Mg的活化能 160~240 kJ/mol H 2 范围,说明稀土和Ni的添加显著降低了镁合金的反应能垒。对于该合金的放氢反应,则可以通过化学反应控速的Chou模型更好地拟合,计算的特征时间分别为8.8 min(564 K)、3.0 min(588 K)和 1.5 min(620 K),说明放氢速率也随温度升高而增大。放氢活化能是 97.5 kJ/mol H 2 ,也远比纯MgH 2 和其他镁合金要低。
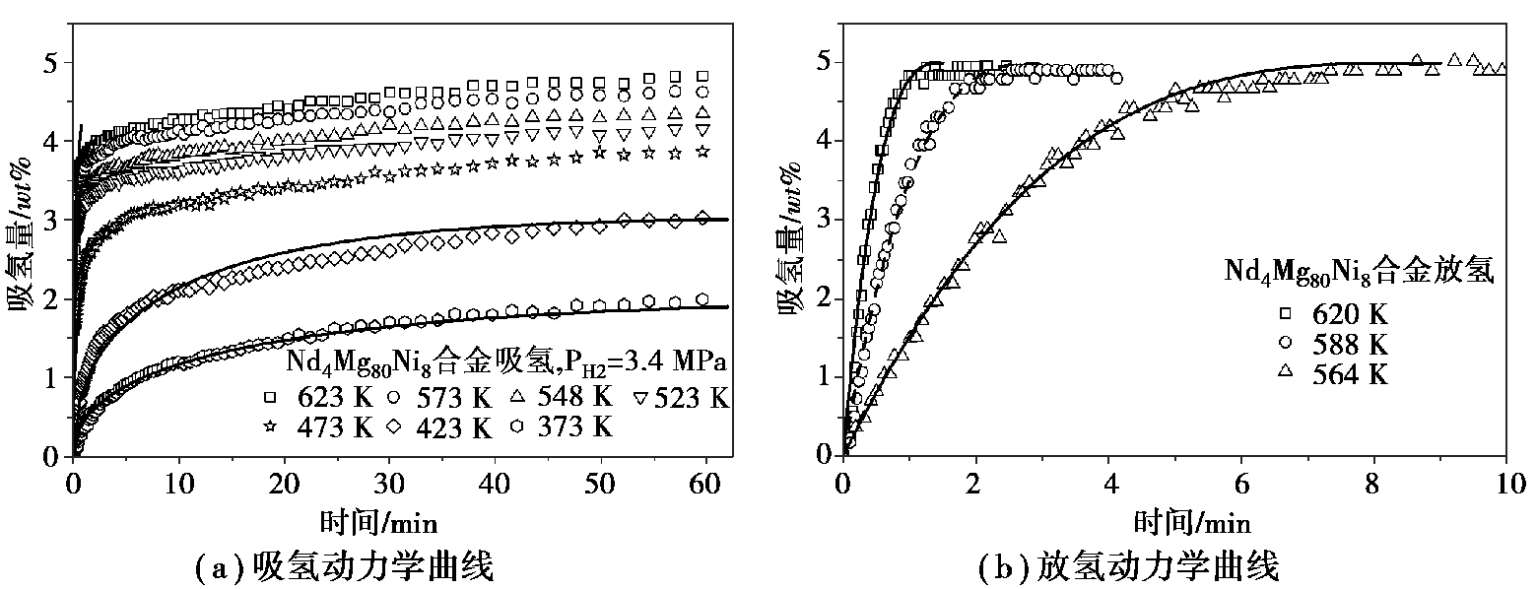
图 2.10 Nd 4 Mg 80 Ni 8 合金在不同温度下的吸氢和放氢动力学曲线