




在推理问题中,我们希望在给定一些观察到的 证据变量 (evidence variable)的情况下,推断出 查询变量 (query variable)的分布。其他节点被称为 隐藏变量 (hidden variable)。我们通常将查询变量上的分布称为在给定证据情况下的 后验分布 (posterior distribution)。
为了说明推理中所涉及的计算,请回顾一下示例2-5中的贝叶斯网络,其结构如图3-1所示。假设我们将 B 作为查询变量,证据变量为 D =1和 C =1。推理任务是计算 P ( b 1 | d 1 , c 1 ),即在给定观测到的轨迹偏差和通信损失的情况下,计算电池故障的概率。
根据式(2.22)中引入的条件概率的定义,可以得出:
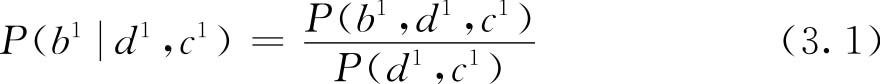
为了计算分子的值,我们必须使用一个称为 边缘化 (marginalization)的过程,即对未涉及的变量(在本例中为 S 和 E )进行汇总:
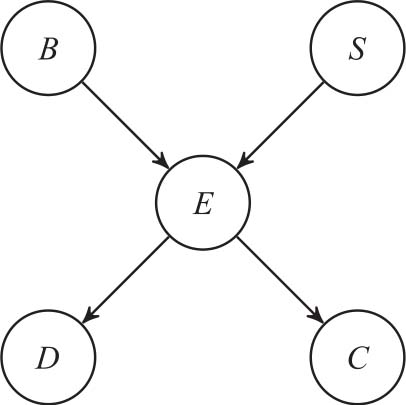
图3-1 来自示例2-5的贝叶斯网络结构
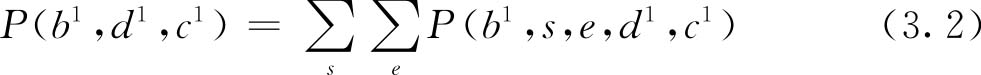
根据式(2.31)中引入的贝叶斯网络的链式规则,可以得出:
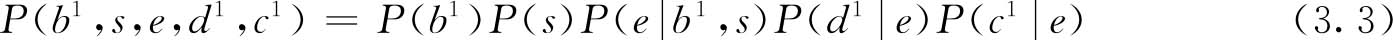
公式右侧的所有分量指定为与贝叶斯网络中的节点相关联的条件概率分布。我们可以使用相同的方法计算式(3.1)中分母的值,但需要对 B 的值进行额外的求和。
使用条件概率定义、边缘化以及应用链式规则的过程可以用于任何贝叶斯网络中执行精确的推理,我们也可以使用因子来实现它。回想一下,因子代表离散的多元分布。我们使用以下三种因子操作来实现:
● 可以使用 因子的乘积 (factor product,算法3-1)来组合两个因子,以产生更大的因子,其范围是输入因子的组合范围。如果我们有 ϕ ( X , Y )和 ψ ( Y , Z ),那么 ϕ · ψ 将覆盖范围 X 、 Y 和 Z ,其中( ϕ · ψ )( X , Y , Z )= ϕ ( X , Y ) ψ ( Y , Z )。示例3-1中展示了因子乘积的过程。
算法3-1 因子乘积的一种实现。算法构造了表示两个较小因子(ϕ和ψ)联合分布的因子。如果我们想计算ϕ和ψ的因子乘积,则只需要使用表达式ϕ*ψ


示例3-1 演示如何将表示为 ϕ 1 ( X , Y )和 ϕ 2 ( Y , Z )的两个因子组合在一起,生成表示为 ϕ 3( X , X , Z )因子的因子乘积,计算过程如图3-2所示。
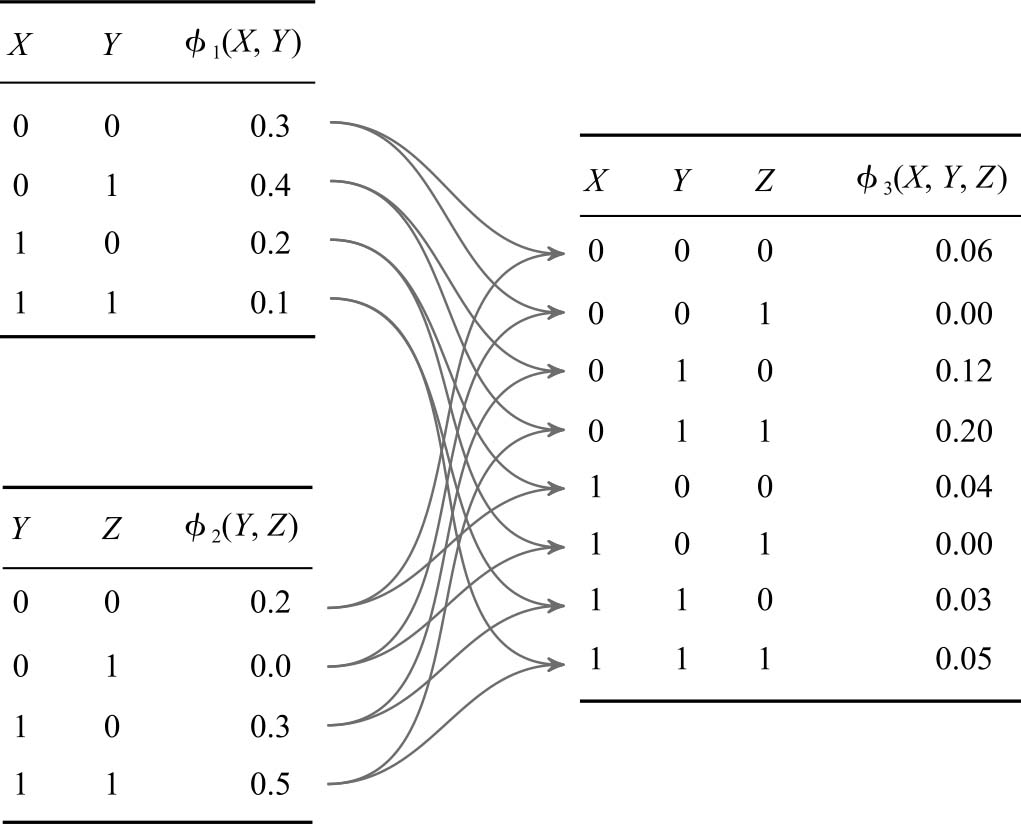
图3-2 因子乘积的计算过程
● 在整个因子表中,可以使用 因子边缘化 (factor marginalization,算法3-2)对特定的变量进行汇总,并将其从结果范围中删除。示例3-2演示了因子边缘化的过程。
算法3-2 将名为name的变量通过因子ϕ边缘化的一种方法

示例3-2 演示因子边缘化 。回顾表2-1中的联合概率分布 P ( X , Y , Z )。对于 X 和 Z 具有匹配赋值的每一行,我们可以通过将每一行的概率求和来对 Y 进行边缘化,边缘化的过程如图3-3所示:

图3-3 因子边缘化的过程
● 可以针对某些证据使用 因子条件化 (factor conditioning,算法3-3)来删除表中与该证据不一致的任何行。示例3-3演示了因子条件化的过程。
算法3-3 根据给定证据实现因子条件化的两种方法。第一个函数带一个参数,即一个因子ϕ,并返回一个新的因子,其表中的数据项与值为value的变量name一致。第二个函数带一个参数,即一个因子ϕ,并以命名元组的形式应用证据。如果一个名为name的变量在因子ϕ的范围内,则in_ scope方法返回true

示例3-3 演示如何设置证据。在本例中, Y 是一个因子,结果值必须重新归一化 。因子条件化包括删除与证据不一致的各个行。以下是来自表2-1中的因子,我们假设 Y =1。删除 Y ≠1的所有行,过程如图3-4所示:
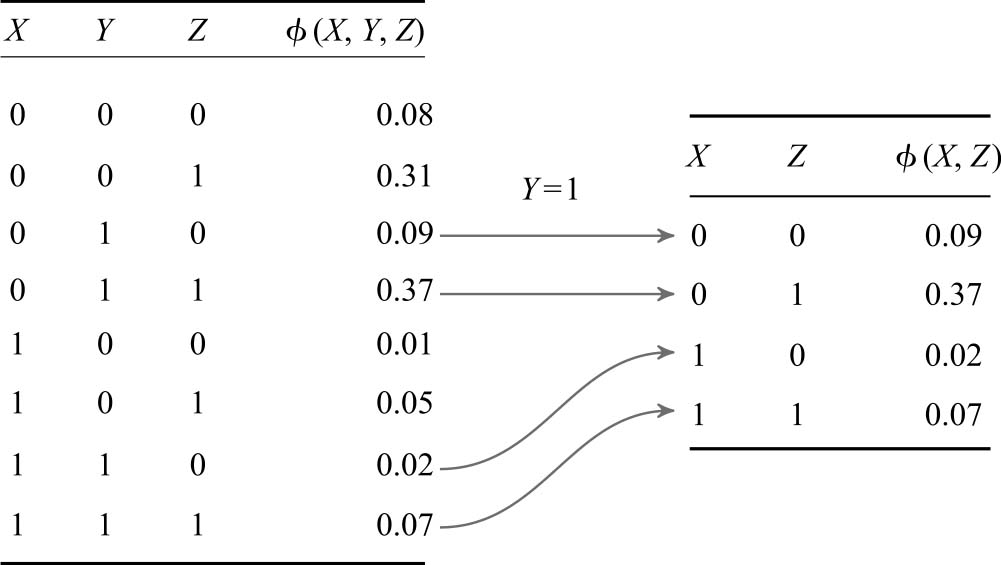
图3-4 因子条件化的删除过程
在算法3-4中,上述三种因子运算被综合使用以执行更精确的推理。算法首先计算所有因子的乘积,并以证据为条件,边缘化被隐藏的变量,然后进行归一化操作。这种方法产生的一个潜在的问题是所有因子乘积的大小规模。因子乘积的大小规模等于每个变量假设值的乘积。对于卫星监测示例问题,只有2 5 =32个可能的赋值;但对于许多相关的问题,其因子乘积可能会过于庞大,从而无法进行枚举计算。
算法3-4 一种用于离散贝叶斯网络bn的朴素精确推理算法。该算法将一组查询变量query以及与观测变量关联的证据evidence作为输入。算法以因子的形式计算查询变量的联合分布。我们引入ExactInference类型,以允许使用不同的推理方法调用infer,我们将在本章的其余部分中讨论其他推理方法
