




通常,人们习惯于在时间域研究信号幅度(因变量)与时间(自变量)的关系。而在通信领域还常常需要了解信号幅度和相位与频率(自变量)之间的关系,即要在频率域中研究信号。因此,这一讲就聊聊信号和系统在频率域的特性问题。
需要声明两点,一是通信原理课程中,不严格区分频率 f 和角频率 ω ;二是术语“函数”和“信号”可以互换,信号可认为是具有物理意义的函数。
用于通信的信号大多包含多个频率分量,比如一个周期方波信号就是由不同频率的正弦信号分量叠加构成。生活中,一架钢琴的88个键分别对应88个不同频率的声波,当演奏者按下一个和弦时,所发出的声波就是几个单音声波的合成,如图1-23所示。
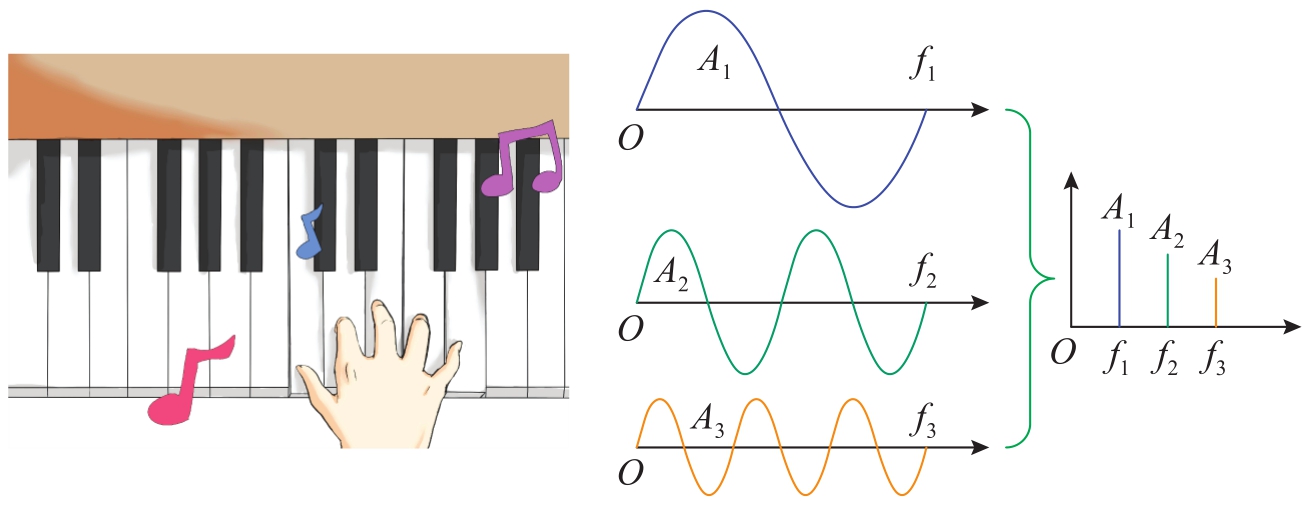
图1-23 和弦的频谱图
在时间轴上看,该声波是一个幅度不停变化的曲线,但在频率轴上看,就是几个位于不同频率的直线段(分量信号的幅度)。可以用下面的例子解释这个问题。
假设现在有四个不同频率、振幅和初相的余弦信号,它们的时域表达式分别为
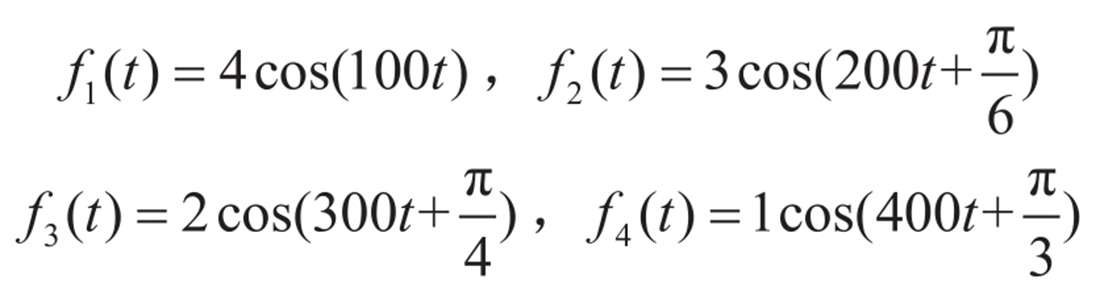
显然,它们都是时间 t 的函数。但是我们注意到,如果把四个信号的振幅和初相看作因变量的话,那么它们和另一个变量——频率 ω 也呈函数关系,如图1-24所示。
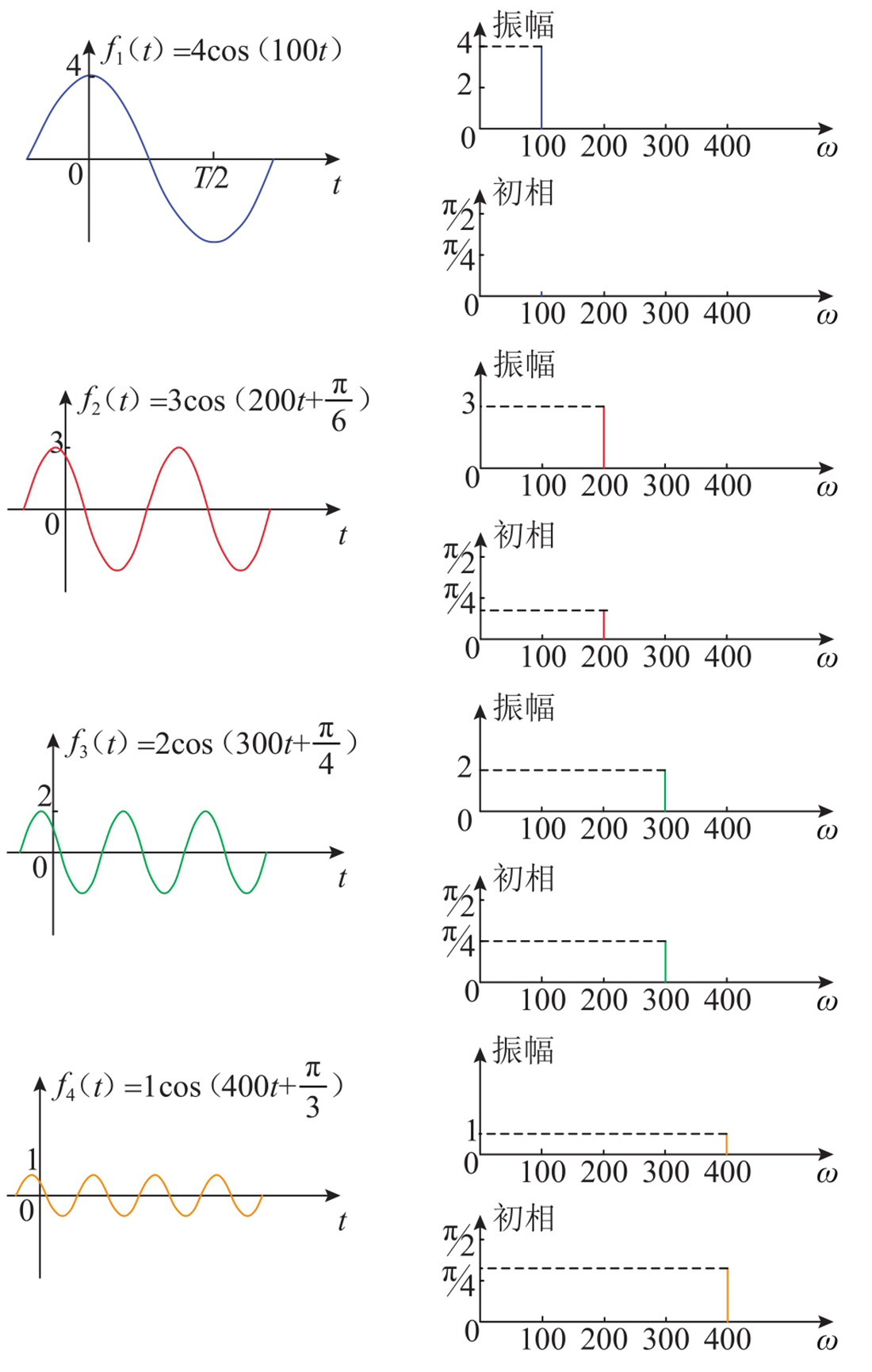
图1-24 正弦信号时域及频域波形
可见,振幅与频率构成一个函数,简称“幅频函数”,相位(初相)与频率也构成一个函数,简称“相频函数”。也就是说,任意一个正弦信号除了时域波形外,还可用幅频波形和相频波形在频域中表示。简言之,正弦信号的频域波形(频谱)由幅值和初相两个垂直线段构成。
注意:通常,幅频波形和相频波形要分开画。只有当相频波形只取0和π两个值时,两者才可以画在一起。
若把上述4个信号加起来,就构成信号 f 5 ( t ),即有
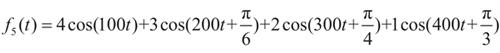
其时域波形如图1-25(a)所示。而在频域,把图1-24中的4个幅频函数和4个相频函数分别相加,即可构成 f 5 ( t )的幅频函数和相频函数,见图1-25(b)。显然, f 5 ( t )的幅频函数和相频函数呈谱线状波形,类似大家熟悉的光谱波形。因此,也被称为“幅频谱”和“相频谱”,二者可统称为“频谱”。
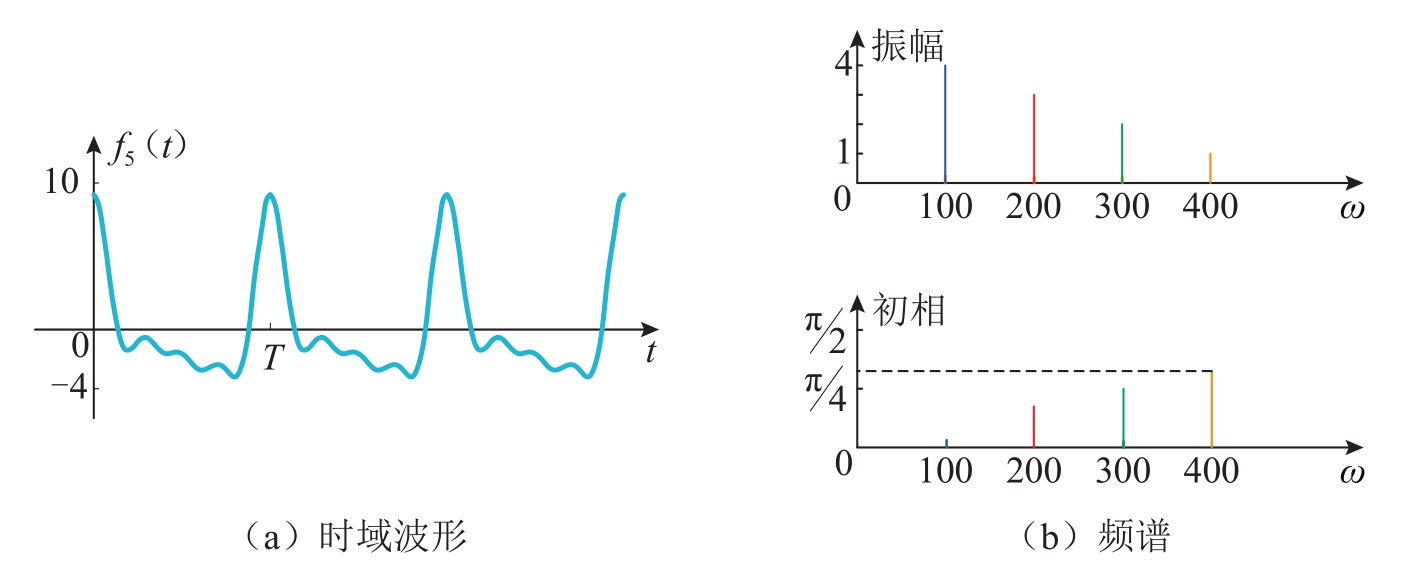
图1-25 合成信号 f 5 ( t )的时域波形及频谱
图1-26给出了一个时域方波及其频谱。图1-27给出了白光的光谱分解示意图。
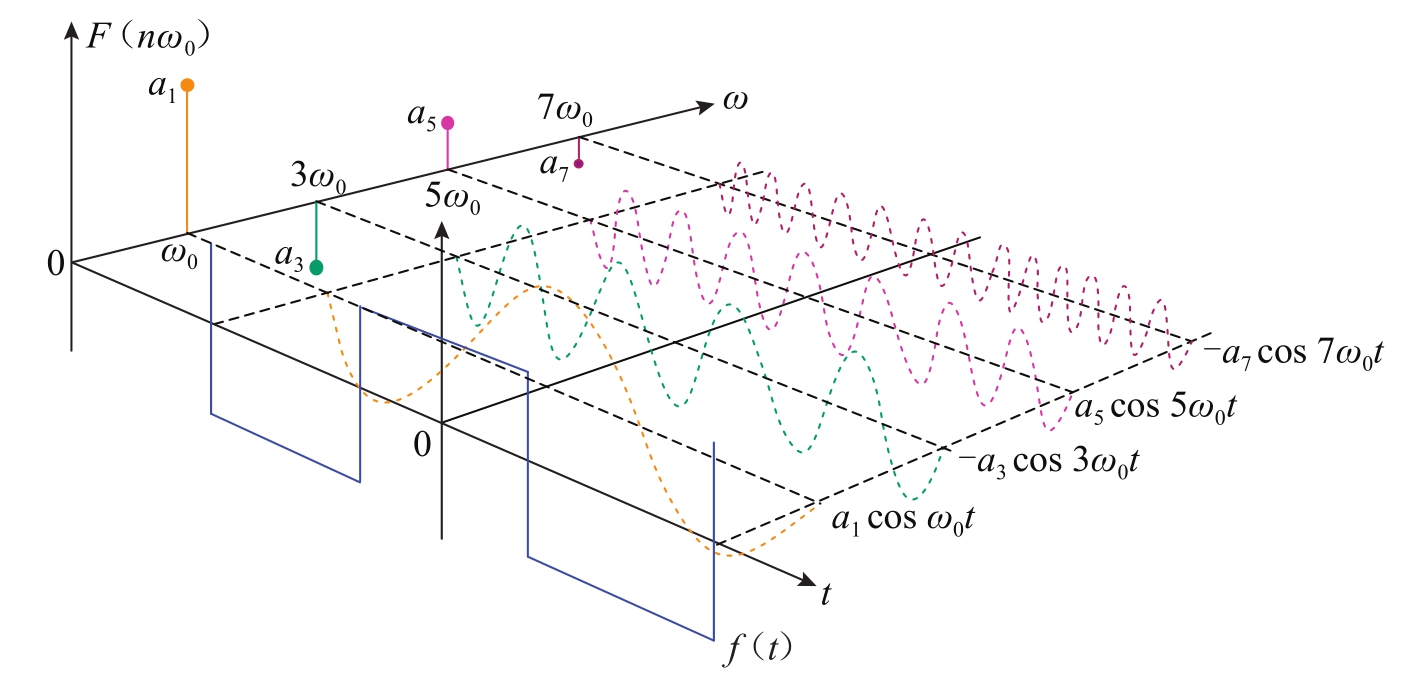
图1-26 对称方波的时域和频域波形
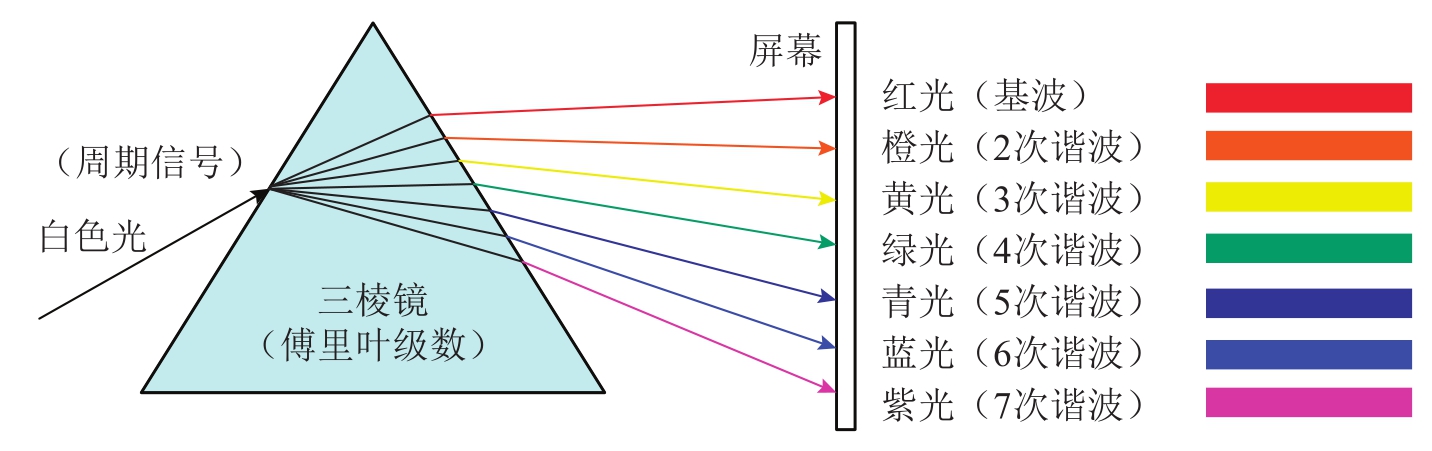
图1-27 三棱镜分光原理图
大家知道,通信就是信号在信道中的传输过程。因为信号都有频谱,所以信道的频率特性会直接影响信号的传输质量。这个概念类似于道路的不同质量指标(比如宽度、平整度等)对车辆行驶产生的不良影响。
车辆需要在宽度大于车宽的道路上才能正常行驶,同样,信号也需要在频率宽度大于信号频谱宽度的信道或系统中才能不失真传输。这个信道或系统的频率宽度就叫“通频带”。
若把一个幅值恒定、频率连续可调的正弦信号加到一个信道的输入端,那么当把该信号的频率从小到大连续改变时,所对应的信道输出信号与频率的变化关系就是信道的频响特性。频响特性可分为两种。
幅频特性:输出信号幅度随频率变化的关系。
相频特性:输出信号相位随频率变化的关系(它反映了输出对输入的延迟)。
在多数情况下,人们只关心信号幅频特性,因此,把信道输出信号幅频率特性也称为频率响应曲线。大多数信道的频响曲线都是带通型的,也就是说,信道对某一频率段的信号幅度影响不大且基本上一致,而对大于或小于该频率段的信号衰减很大,甚至到零,其曲线形状像一个不太规则的“扁方形门”。
通常,以幅频曲线的最大值为标准(一般是曲线中心频率所对应的值),定义通频带如下。
通频带:信号幅度值下降到最大值的 70% 时所对应的两个频率之间的频段。
其中,低频率点叫“下截止频率”,高频率点叫“上截止频率”。因为这两点的幅值与最大值之比为0.7,对应的分贝值是-3(dB),所以,截止频率也叫“3分贝频率”,通频带也叫“3分贝带宽”,见图1-28。从概念上讲,通频带是指一个信道为信号传输所能提供的频带宽度。注意:“分贝”原是一个衡量声压强度的单位。
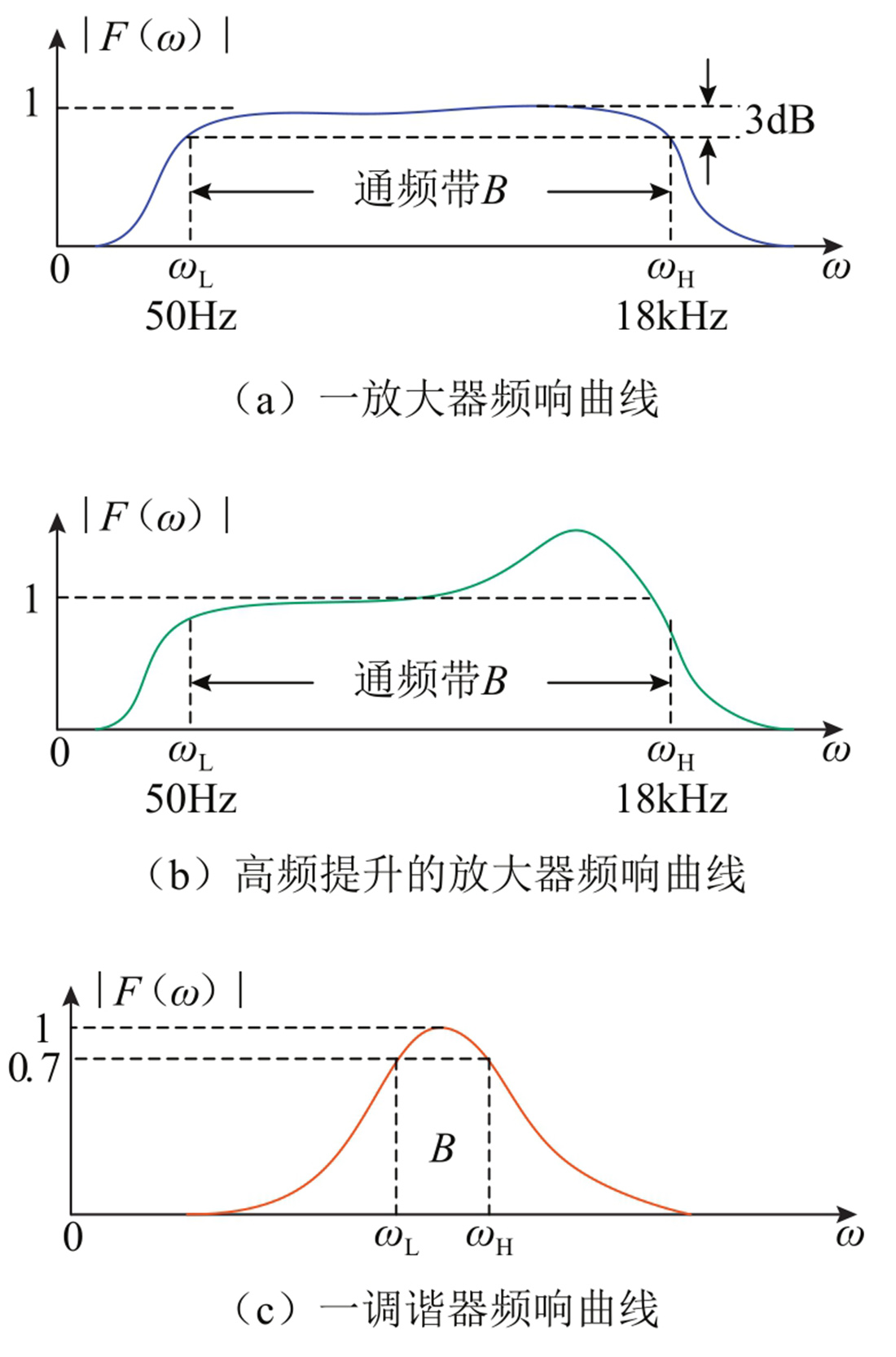
图1-28 通频带实例示意图
对一般传输信道而言,人们希望通频带越宽越好(对于模拟信号来说,意味着频分复用的信号路数就越多,或者信号的保真程度就越高;对于数字信号来说,意味着波特率就越大,可以传输更多的信息),频响曲线越平越好(输出信号的一致性好)。比如高保真音响设备(主要包括音源、放大器和音箱三部分),就要求各部分的频响曲线在通频带内尽可能平,否则,在听音乐时就可能会出现特别强的笛声或特别弱的鼓声,因为某一频率的放大量比其他频率大得多或小得多。同时,还要求通频带在低频段最好低于20Hz,在高频段最好高于20kHz,这是因为音频的范围为20Hz~20kHz,如果音响设备的通频带达不到这个要求,人们就听不到震人心魄的低音鼓声和清脆悦耳的三角铁声。
显然,信号的高保真(Hi-Fi)传输除了要求信道通频带大于信号带宽之外,还必须要求通频带内的频响特性保持平坦,见图1-28(a)。如果放大器的通频带变成图1-28(b)形状,则在播放音乐时,就会感觉到高音部分特别强,即高频信号出现了失真。
生活中很多音响设备,比如汽车音响、家庭影院等都设有音调控制旋钮或均衡器。音调控制旋钮的作用就是人为地改变放大器频响特性,提升或降低音频信号中的某些频率成分(通常是高音、中音或低音部分),以满足人们的不同听觉需求;而均衡器是通过改变多段频响曲线的方式,以弥补放大器频响特性的不平坦或起到与音调控制旋钮相同的作用。
在应用中,也有要求通频带窄一点的场合,如收音机、电视机和电台等设备中的调谐电路以及一些带通滤波器为提高选择性都希望通频带尽可能地窄,如图1-28(c)所示。
信号频谱宽度可类比汽车的车身宽度,信道通频带可类比道路宽度。显然,一条道路要想让汽车顺利通过其宽度必须大于车身宽度,否则,车辆就无法在道路上行驶;而信道通频带小于信号带宽时,虽然信号仍可在信道中传输,但已丢失了很多信息,信号在信道中是以失真的形式传输,就好像把汽车超宽部分切掉在路上跑一样。因此,一条信道要不失真地传送一个信号,必要条件就是其通频带大于信号的频谱宽度。

(1)频谱就是信号幅度(或相位)随频率变化的关系(图)。
(2)任何一个用于通信的信号都有频谱。通常包含幅度谱和相位谱。
(3)任何一个工程信号的频谱都有一定的频率宽度,类比运输车辆的宽度。
(4)要保证信号在通信系统中不失真传输,就必须保证频谱不丢失、不受损害。
(5)在通信领域,人们还关心信号能量或功率的大小随频率的变化关系,比如随机信号和噪声,这就引出了能量谱和功率谱的概念。通常,对于能量信号用能量谱描述,而功率信号用功率谱描述,它们的概念与频谱类似。
(6)通信系统或信道的通频带是衡量通信任务完成质量或系统性能的重要指标。

 圆圆
老师,信号的时域波形我们在示波器上见过,可信号的频谱在哪儿能看到?
圆圆
老师,信号的时域波形我们在示波器上见过,可信号的频谱在哪儿能看到?
 皮皮
在一种名叫频谱仪或频率分析仪的仪器上可以看到。它的长相跟普通示波器差不多,甚至有的就是二合一,见图
1-29
。
皮皮
在一种名叫频谱仪或频率分析仪的仪器上可以看到。它的长相跟普通示波器差不多,甚至有的就是二合一,见图
1-29
。
图1-29 频谱分析仪

 静静
老师,通频带与道路宽度的类比我理解了,但道路平整度怎么类比呢?
静静
老师,通频带与道路宽度的类比我理解了,但道路平整度怎么类比呢?
 皮皮
前面说过,可以类比衰减。比如,如果道路的路面平整,车辆行驶过程就平稳快速,磨损小,货物损坏率也小;若不平整,行驶速度慢,颠簸大,磨损大,货物损坏率也大。若信道幅频特性不平坦,则不同频率分量会有不同的衰减(类似于磨损),引起信号失真(类似货物破损)。明白了吗?
皮皮
前面说过,可以类比衰减。比如,如果道路的路面平整,车辆行驶过程就平稳快速,磨损小,货物损坏率也小;若不平整,行驶速度慢,颠簸大,磨损大,货物损坏率也大。若信道幅频特性不平坦,则不同频率分量会有不同的衰减(类似于磨损),引起信号失真(类似货物破损)。明白了吗?
 静静
明白了。
静静
明白了。
