




区块 是第三种基本技巧。它和排除以及唯一余数不同的地方在于,区块技巧需要你用一种组合的思维来进行理解。
和排除相同,区块也分三种: 宫区块 、 行区块 和 列区块 ,其中,行区块和列区块可以统称 行列区块 。我们先来看宫区块。
如右盘面所示。我们这次可不能直接得到结论了。
先来看看第6宫,我们可以发现什么?借助一下我们之前学过的宫排除,数字8在第8列已经有了提示信息,因此第8列不能填入别的8了,在第6个宫里,8只能放在DF7
 两个单元格里。
两个单元格里。
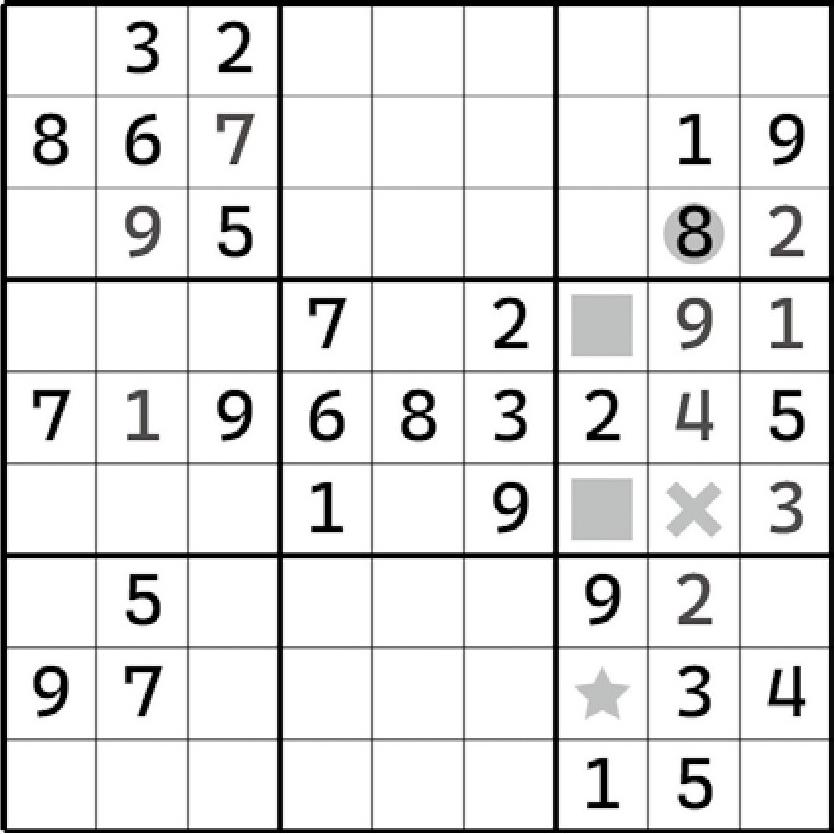
虽然我们不知道具体哪个单元格填入8,但是DF7同在第7列上。“同在第7列”有什么用吗?有的。它意味着无论哪一格填8,第7列的其他格子都不可能为8。因为第7列填入8的机会只能给DF7,而同一列只能填入一次8,因此除了它俩,别的单元格都不可以是8了。
那么,H7<>8
 就是这一阶段得到的结论了。得到这一点还没完,接着我们来看第9个宫。
就是这一阶段得到的结论了。得到这一点还没完,接着我们来看第9个宫。
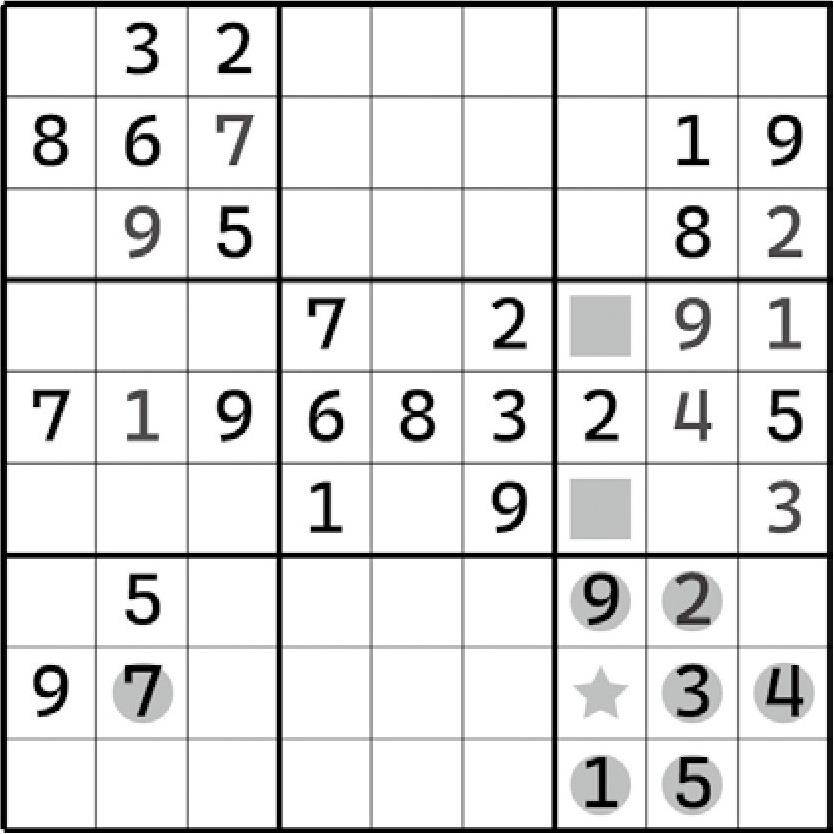
我们使用前面学过的唯一余数技巧来仔细数数H7此时可以填入的情况。
从1数到9我们可以发现,1、2、3、4、5、7、9都是无法填入的数字;而前文又得到了H7<>8,那么H7只能是6了。因此,H7=6就是我们使用这个思路得到的填数结论了。
我们把第6个宫形成的这个数字8的“模棱两可的”两个格子DF7称为
区块结构
,而把使用DF7(8)
 的区块结构称为
区块技巧
。由于这个区块结构是通过宫排除得到的,DF7也是从第6个宫作排除而形成的区块结构,因此我们称这样的技巧为宫区块技巧。
的区块结构称为
区块技巧
。由于这个区块结构是通过宫排除得到的,DF7也是从第6个宫作排除而形成的区块结构,因此我们称这样的技巧为宫区块技巧。
接下来我们来说说,观察起来比较痛苦的行列区块。
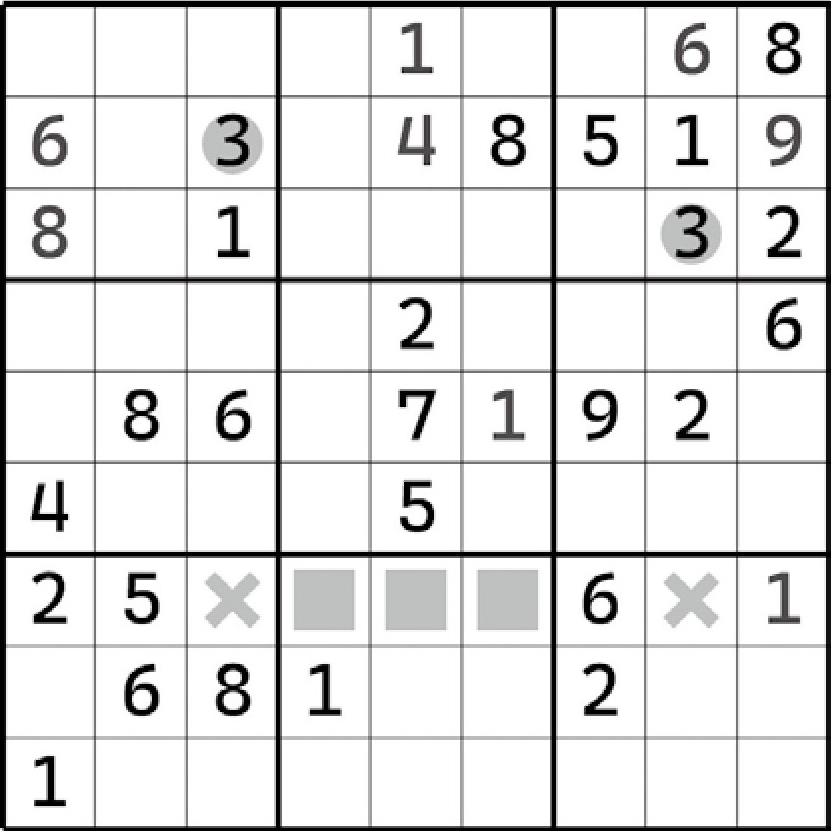
如上盘面所示,此时我们把视角聚焦于第7行。我们使用行排除,虽然得不到合适的结果,但是仔细看就可以发现,3的可填位置在同一个宫里:第8个宫。
虽然我们并不知晓具体是G4、G5,还是G6最终填入3,但是由于它们同属于第8个宫,而第8个宫里又必须填一个3进去,所以填入3的机会就只能给G456三个格子了,否则第7行就无法合理安排3的填数位置了。
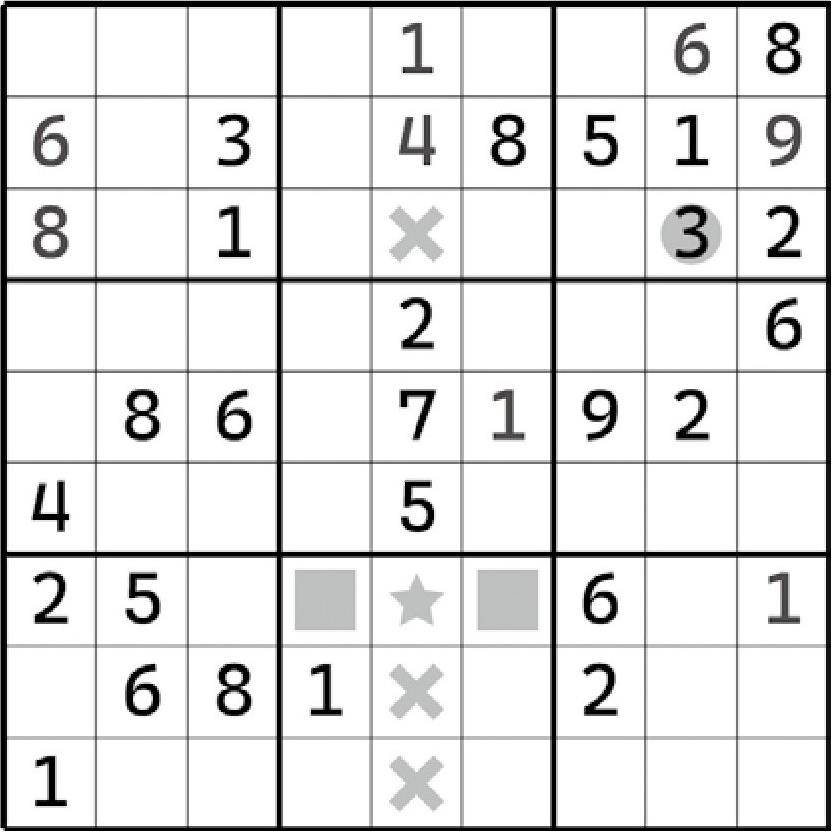
G456里必须有一个3,那么,第8个宫的别处任何一个单元格都不能是3了。
如上盘面所示,我们利用前文得到的结论,将视角切换到第5列就可以得到和确定3的具体位置了。
首先,按照基本的排除,C5<>3,因为第3行上已经有3的提示信息了,我们可以复用C8的数字3。而HI5<>3
 ,这一点是通过前文G456中必须有一个3的结论得到的。“第8个宫的别处任何一个单元格都不能是3”,还记得吧?因此,第5列里唯一可以填入3的地方就只能是G5了。
,这一点是通过前文G456中必须有一个3的结论得到的。“第8个宫的别处任何一个单元格都不能是3”,还记得吧?因此,第5列里唯一可以填入3的地方就只能是G5了。
有些小伙伴会觉得奇怪,这次的结论怎么能出现在前文用过的G456里呢?G456不是还不能确定结果吗?实际上,我们这时已经将视角切换到了第5列而没有再去关注第7行了。第7行的3的分布只能让我们得到“G456里有一个3”的结论,而在第5列通过基本的列排除技巧就可以唯一确定3的位置。所以,这里的3并不是看G456得到的,而是根据第5列的列排除得到的。不然,这个3还能放在第5列的哪里呢?数独不是就要求,每一行、每一列、每一个宫都要有完整的一套1~9吗?第5列就属于“列”的一员。
所以,这个题的结论就是,G5=3。这个技巧用到的是从第7行确定的G456区块结构,因此称为行区块结构。
列区块的形成和行区块是完全一样的,只不过是从行改成了列而已,因此就不再单独举一个例子给大家介绍了。这里留一个列区块技巧的例题,希望你可以自己推理。
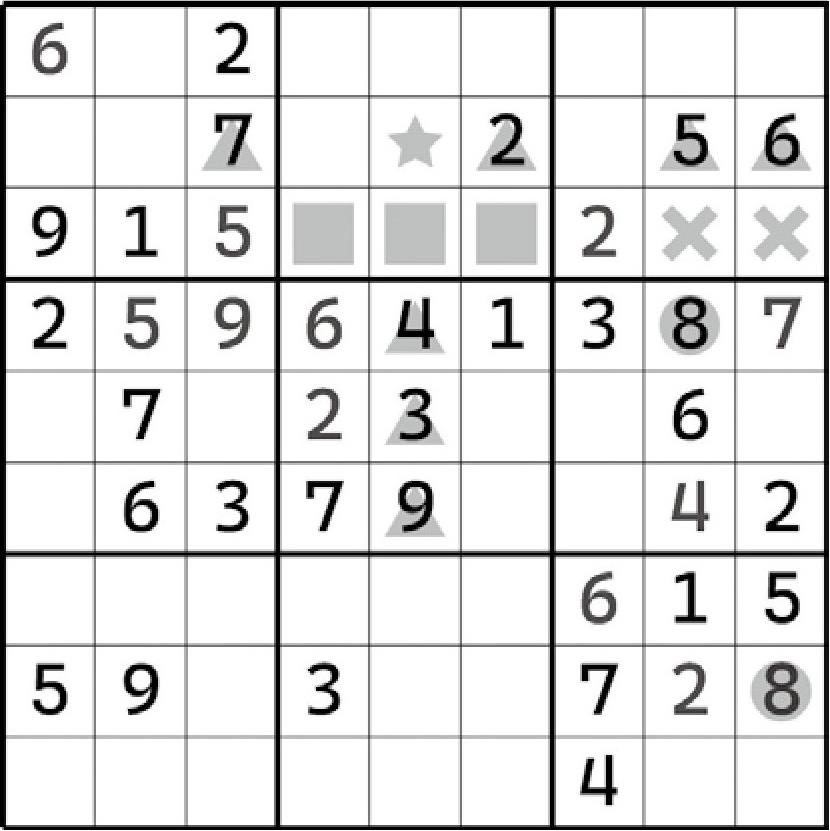
如上盘面所示。这个题目的结论是使用了一个区块之后,通过唯一余数得到的。
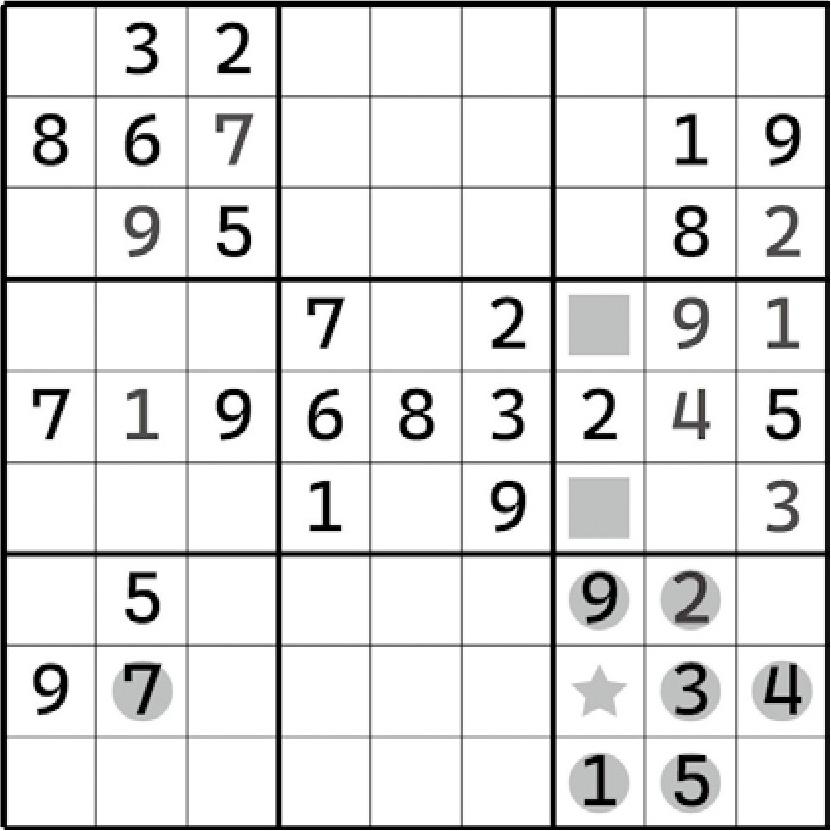
实际上,在前文举例说明的这些题目里,大家都可以发现一个基本的、相同的找寻规则——直接按排除法来找它们就行了。是的,区块结构的形成,实际上就是“模棱两可版”的排除法结论。只是,这样的区块结构可以更好地约束这些格子的填数,可以影响到别的区域。例如区块部分提到的第一个例子(上盘面):我们可以发现,虽然区块是从第6宫得到的,但是它影响到了第7列。
再比如这个例子:
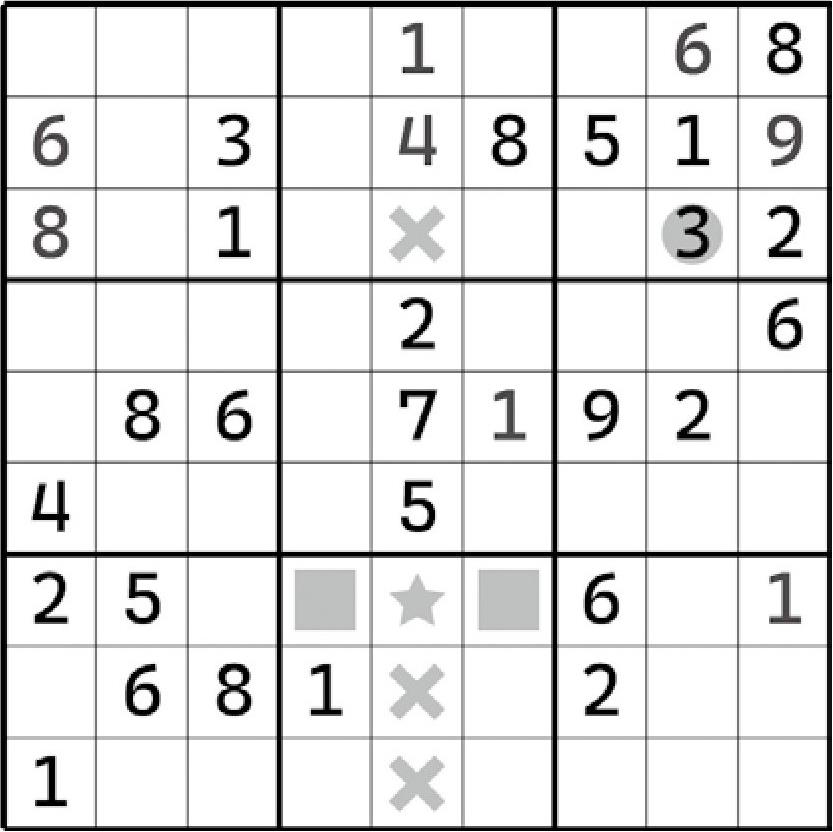
虽然区块是通过第7行得到的,但是它影响到了第8个宫。
因此, 区块就是一种特殊的排除法 。知道这一点之后,你只需要按照排除的基本找法去找区块就可以了。
还有一种区块,是借用前文说到的两种区块类型,组合使用的新区块“品种”。我们称为 组合区块 (或 级联区块 [1] )。
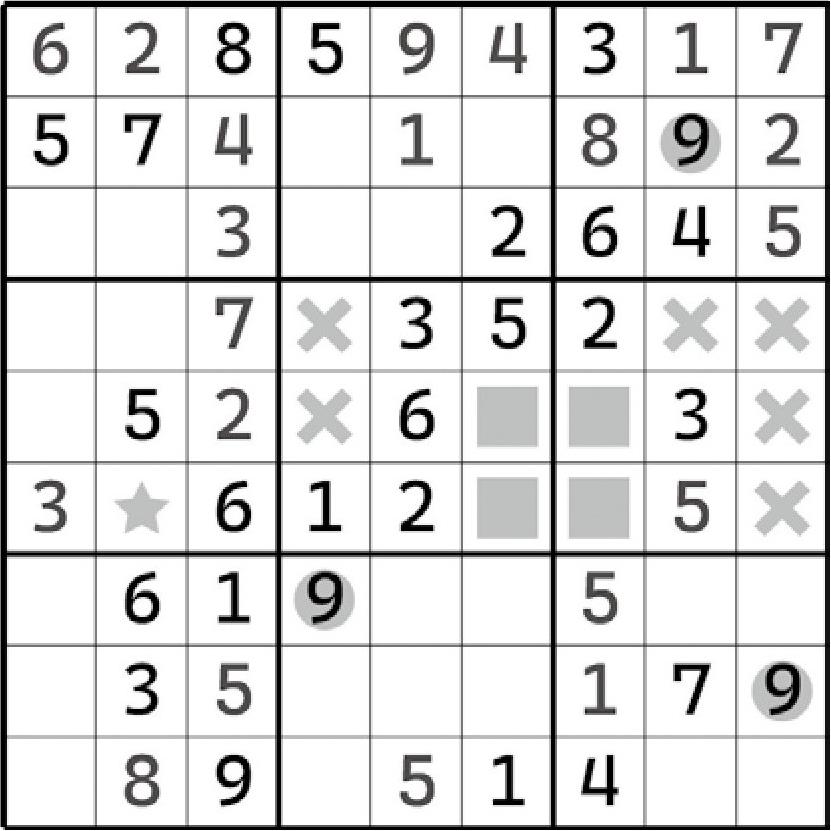
如上盘面所示,我们这次一次观察两个宫区块。第一个宫区块在第5宫,第二个宫区块则在第6宫,它们都是数字9的区块结构。
如果我们将两个数字9的宫区块凑成一对,直接一起看会有什么效果呢?想一想,这两个区块的分布有没有什么特殊的地方?是不是两个区块结构涉及的4个单元格刚好凑成两行两列?那么,F2可以填入9吗?不能。虽然这两个宫区块跟F2好像毫无关系,但是实际上,如果我们去列举一下9在第5、第6个宫的完整填数可能,就会发现,最终只有两种填法:
●E6和F7同时是9。
●E7和F6同时是9。
除此之外,别无其他。因为数独要求不能在同一行列上出现重复项,所以9在这两个宫区块里就只能放在“对角关系”的两个格子里。这里要注意一个小细节:区块结构最终是必须要有一个正确的数字填入进去的,所以两个宫区块应该必须有两个9的填入才是正确的。那么,两个9的摆放只能是斜着来了,否则一定会导致行或列出现数字9的重复项,违背数独规则。
那么,无论怎么放,9在第6行里也只能放在F67两个单元格。为什么呢?因为两个宫区块只有两种可能的正确摆放情况,而无论是哪种,F67里面必定会出现一次9,而巧妙就巧妙在,它们位于同一行。位于同一行意味着第6行可以放入9的位置只有F67,别的格子就不可能是9了。F2也是第6行的,所以F2<>9。同理,E1<>9。不过这次就不再看第6行,而是看第5行了。
我们继续深入。基于F2<>9,我们可以得到一个唯一余数的结论。
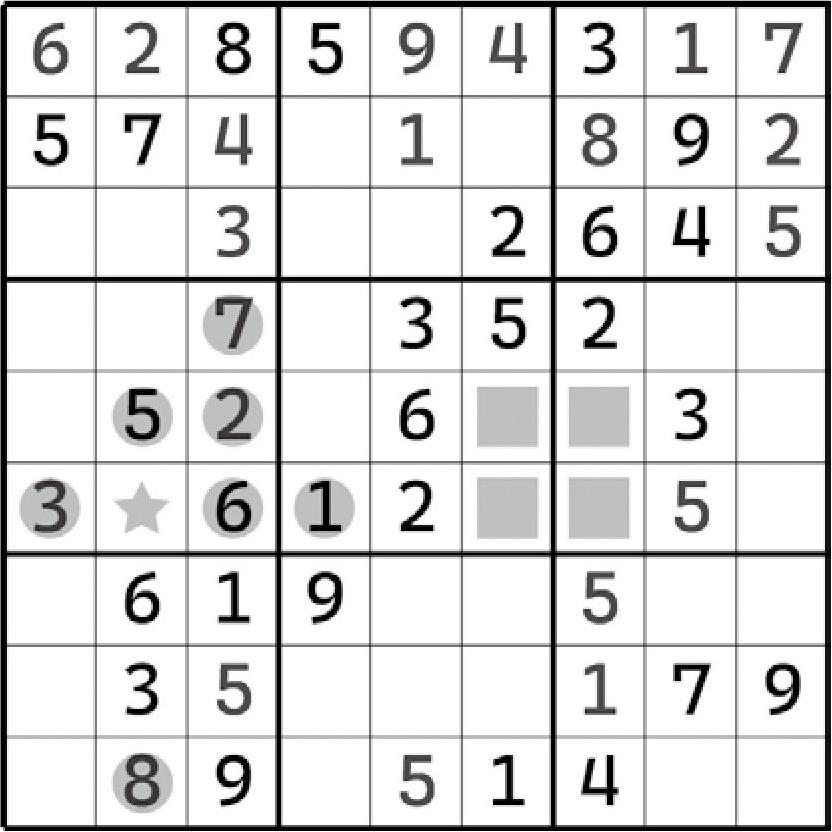
如盘面所示,我们将视角聚焦于F2。F2此时还能填入数字几呢?只能是4了。首先,1、2、3、5、6、7、8都不能填入,这是基本的排除规则;而F2<>9前文已经得到了,用到的是两个宫区块组合起来看的思路。那么,F2此时只剩4可以填入,所以F2=4就是结论了。
我们就把刚才得到的涉及第5、第6个宫的、关于数字9的区块结构称为组合区块,表示它们是组合起来使用的逻辑。
细心的小伙伴可以发现,这个题目中还藏着一个行区块(下图),根据它可以直接得到E1和F2不填9的结论,而根本不需要如此绕远。
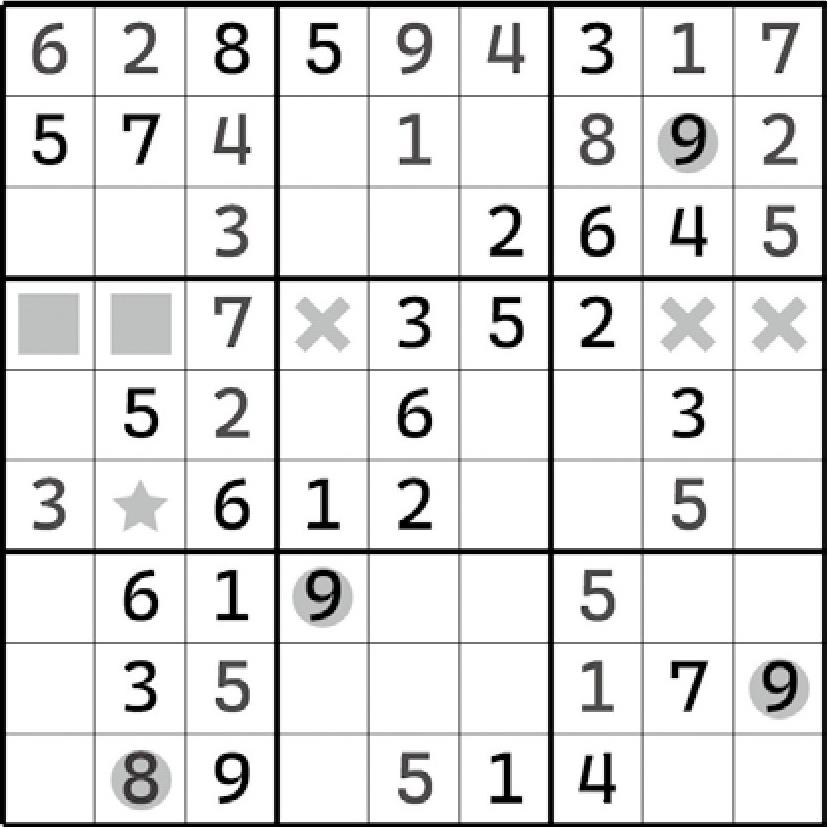
那么,组合区块存在的意义究竟是什么呢?既然有代替的、更简单的区块结构,为什么又非得这么去找呢?
实际上,组合区块存在的意义在于观察层面。如果你对行列区块或者行列排除并不熟练的话,可能并不能直接观察到题目中存在的这个行区块结构。而宫区块和宫排除是观察起来难度比行列区块和行列排除要低的技巧类型,因此我们一直而且总是建议大家优先找宫排除和宫区块技巧。
在个题目里,我们使用的两个区块都是宫区块,因此非常好找到。而正是因为观察难度低,我们经常会使用这样看似绕远的方式来代替掉一部分的行列排除和行列区块技巧。虽然组合区块结构比起基本的行列排除和行列区块技巧来说要大一些,但是实际上,这种代价是很小的。甚至,我们使用组合区块来替代一部分这样的技巧,可以达到提速的效果。
至此,区块结构就介绍完毕了。
[1] “ 级联 ”一词来自微软公司对一些复合、组合理解的概念。微软将一些同等概念的东西称为级联的。