




欢迎来到标准数独的世界!从现在开始,您将步入标准数独的殿堂,并学习到迄今为止最为专业的数独技巧。不过,如果您还没有任何基础的话,就请跟着我来吧!
数独是一种有趣的益智游戏。它需要您在空格内填入1~9的其中任意一个数字,使得每一行、每一列以及每一个正方形的小九宫格内的数字都不重复。如下面三个数独盘面格子(以后均简称“盘面”)所示(图1-1),分别是行、列和小九宫格(以后均简称为“宫”)不重复的情况。
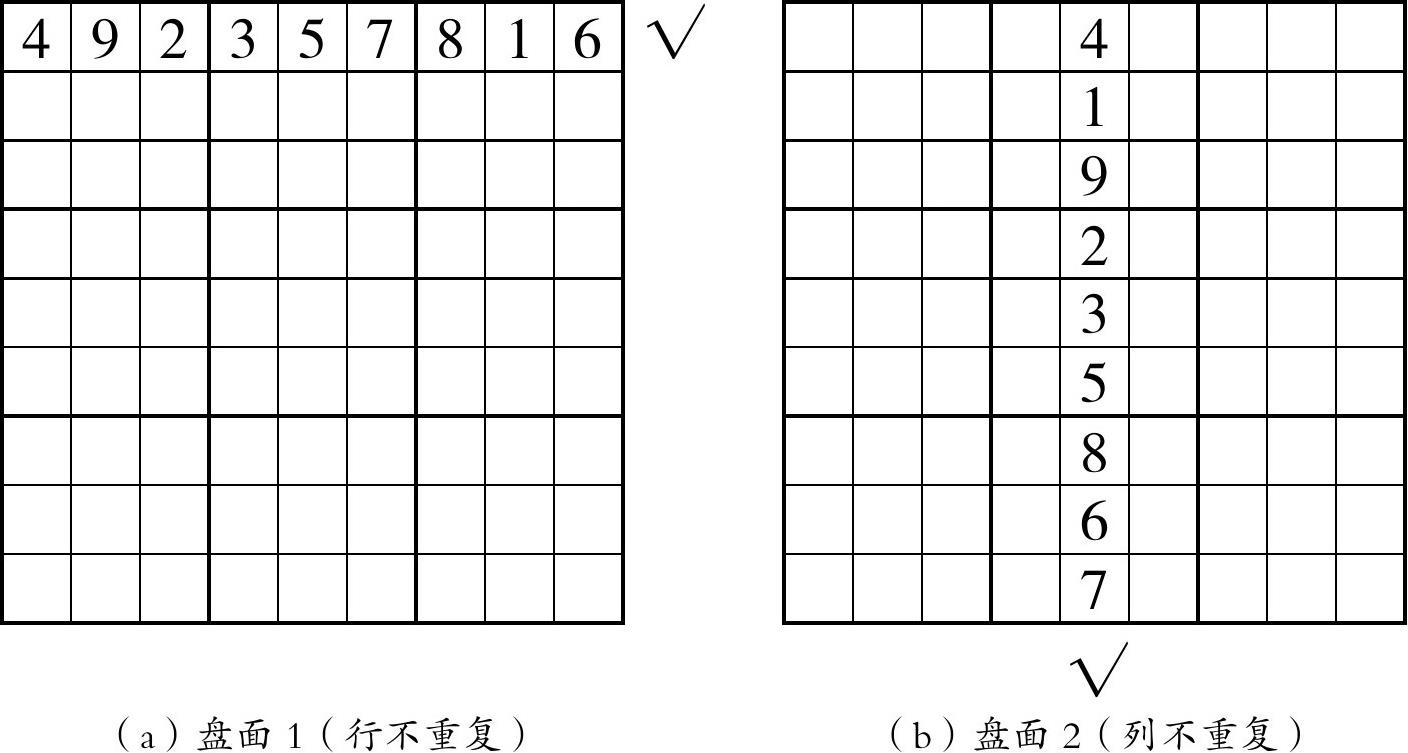
图1-1
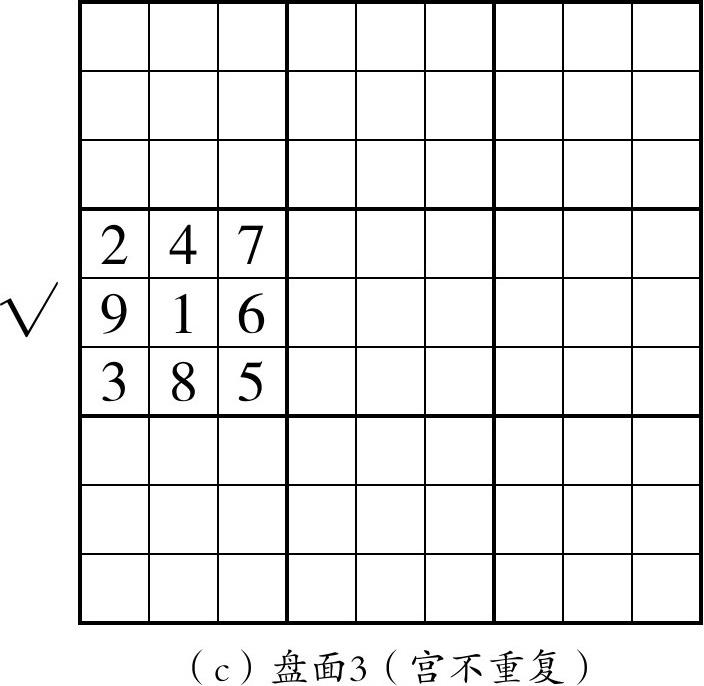
图1-1 数独规则简介
所谓的行,就是每一横排;而列,就是指每一竖列;那么每一个小九宫格(宫),指的是用粗线围住的3×3的九宫格区域。当然,整个盘面的每一行、每一列和每一个宫都得做到像上面三个盘面所示的那样,数字1~9不重复。但是,只要发现某一行、某一列或者某一个宫内有两个数字是相同的,那就一定错了,因为这并不满足数独的相应规则。
数独,顾名思义,数字的出现必须要“独”,也就是不得重复。但是“独”不只有这个意思。数独还有一“独”,那就是任意合格数独盘面都只有唯一的一个答案。也就是说,每一个格子都只有唯一的一种填法,这样才能真正体现数独的“独”的特性这样才叫“独”之道。
请注意一点。图1-1的盘面1到盘面3都不是真正意义上有唯一答案的盘面。因为它给出的几个数并不足以让题目形成唯一的答案。那么在最开始的情况下,就必须得让题目有一定的、能给我们推理的“提示数字”,这样的数字称为提示数或者已知数。那么,初始情况下,至少必须得给出多少个提示数,才可能保证题目只有一个答案呢?这个数字可能会让你觉得匪夷所思——17。不过这个数字具体是怎么求得的,这一点就不在这里展示了,它牵涉到了大量的数学知识。至少有17个提示数,才可能保证题目只有一个答案,但是,这也只能是“可能”保证。因为随机给定17个提示数的题目很可能不具有唯一答案。
后续内容之中,会将“唯一答案”换一种说法,即“唯一解”;含有多个答案的题目称为“多解题”,没有正确答案的题目称为“无解题”。多解题和无解题都是我们应该予以避免的,因为它们是在出题过程中不严谨而导致出错的“劣质题目”。很多时候我们都不能直接从题目看出这题是否有唯一解,所以它们还会耽误大量的时间,这就要求我们去做一些正规出版物中收集的题目。
数独的最早起源一直是备受争议的话题。有人说它最早来源于欧拉的拉丁方块(没有宫的规则的标准“无宫”数独);而有一部分人士说,数独发源于一个工人;也有人称,数独起源于中国的洛书。
我们不能确定谁是对的,但数独的发展的确有很长的历史了。它先是风靡了欧洲和美洲,然后大约在20世纪传入亚洲,并在日本发展和推广。主要做推广的是Nicoli公司。数独最早被称为“填方块”(Number Place),在日本则被称为“数字具有唯一的限定条件(的游戏)”(数字は独身に限る)。由于日文版的名字太长,随后就被简化成两个字——数独,并一直沿用至今。
中国大陆于2006~2007年接触到数独,并在其间派出国家队参与全球比赛,获得靠前的名次;而真正向公众公开推广,则是在2008年。
现在,数独已经广泛进入各大学校,并作为奥林匹克数学竞赛的相关竞赛题目。各大学、中学,甚至小学,也有数独相关社团和数独活动。