




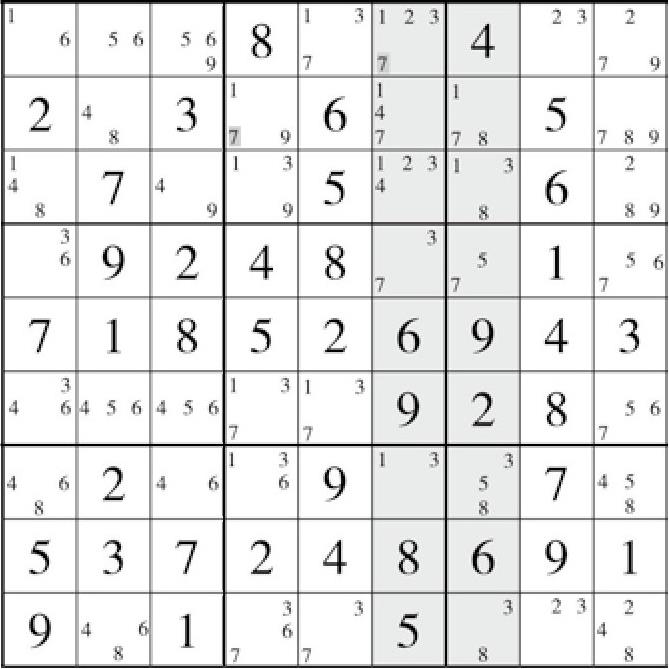
图7-1 盘面30
在盘面30(图7-1)中,我们发现有一个二链列,不过很怪异。
我们很容易地发现,这个二链列的定义域是列6和列7,很明显,删除域是行B和行D。可是不巧的是,这个关于数字7的二链列多出了一格,位于A6。于是尝试消除掉它。
如果A6(7)不存在的话,那么列6和列7就只有B6、B7、D6和D7这4格填入7了,很明显,这样肯定是构成二链列的,那么根据二链列的逻辑推理,删除域应为行B和行D;而如果A6(7)是存在的,那么这个7就会导致行A、列6和宫2内的其余单元格内都不能填入7。
但是列6和列7也就只有这5格可以填,别无其他情况。那么我们就知道,这两种情况必然有一种成立,因此删除掉这两种情况都能够删除掉的位置,我们发现,这两种情况都能删的位置只有B4和B5,而B5已经有数字了,那么只能是B4,因此B4<>7。
这种“差一点”的鱼被称为外鳍鱼,其中那个多出来的单元格被称为外鳍,一般简称为鳍。为什么要叫鳍呢?因为这个技巧本体是鱼结构,那么多出来的就理所当然地被翻译成了鳍。而定义域仍旧是指原定义鱼位置的区域,但删除域则会发生变化:因为现在多了一个鳍,将只能删除掉数个单元格,而不是一整个单元(行、列)了。这一点需要特别注意。
那么,鳍在哪里才能够算作外鳍鱼呢?鳍必须位于鱼的定义域内,且必须位于鱼某个顶点处的同一个宫内。这是为什么呢?因为,我们对标准二链列的推理方式就是选中定义域的其中一个,然后分情况讨论,最终能够得到相同的结论,从而得到删除域,删掉删除域内的单元格的数字。这里多了一个鳍,那么就假设鳍成立和鳍不成立,于是也就分成了两种情况。那么,鳍是否只能是一个呢?当然不是,如下面这个例子中,就有两个鳍。
盘面31(图7-2)就是两个鳍构成的二链列。要么二链列成立,要么旁边的两个鳍成立,虽然很明显,两个鳍不得同时成立,但是目前看来,至少得有一种情况成立。无论是它们中的哪一个,都会导致宫4和行F内的其余单元格都不能填入9了。而此时,行F已经没有可以删除9的位置了,因此只能去看宫4内的位置了。无论是二链列成立还是鳍成立,必然都会使得既在宫4、又在列1内的D1和E1删除掉9。即D1、E1都不等于9。但如果要拥有这样的推理,多个鳍必须位于同一宫内,否则它就不是外鳍鱼了。当然,三链列也同样存在外鳍鱼。
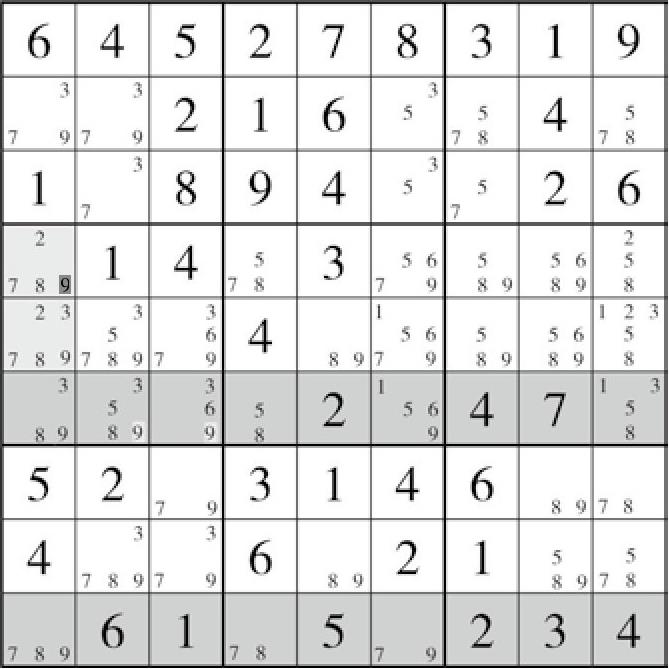
图7-2 盘面31
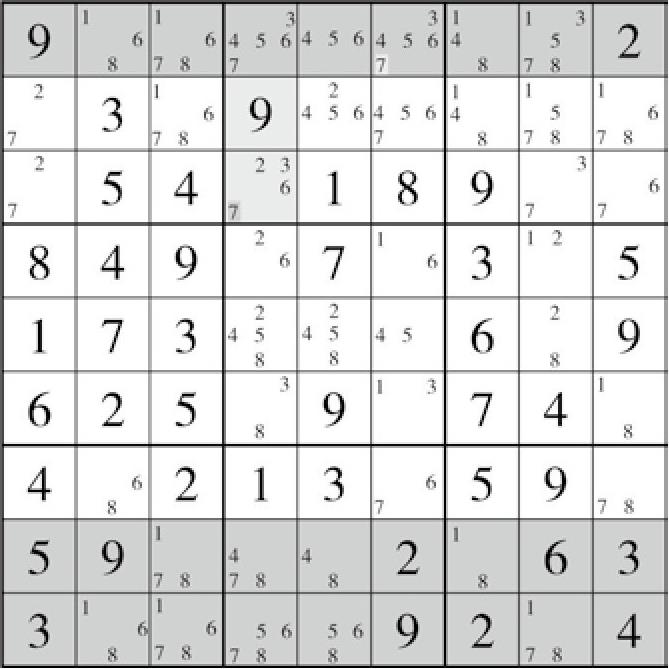
图7-3 盘面32
如盘面32(图7-3)所示。同理,分两种情况,要么是这个残缺的三链列成立,要么是鳍成立。因此删除掉两种情况中都能删除的部分,即C4(7)。
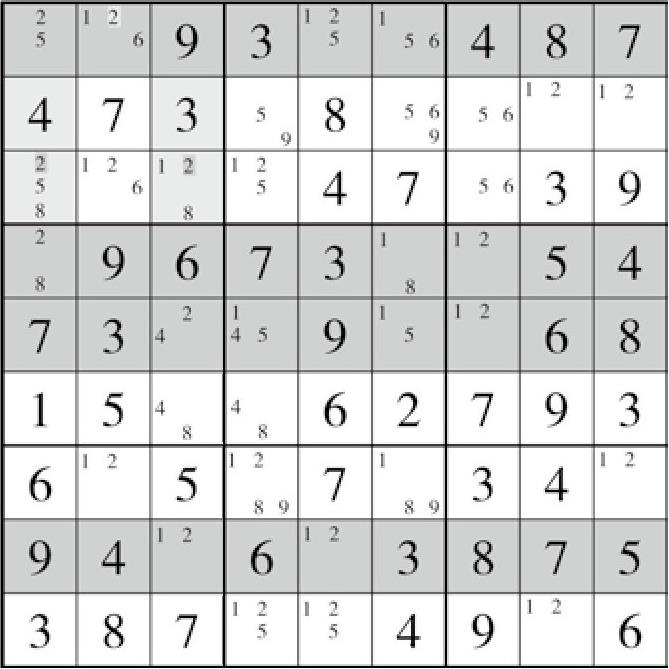
图7-4 盘面33
盘面33(图7-4)所示的为外鳍四链列。分两种情况,要么是残缺的四链列成立,要么是这个鳍成立。因此删除掉两种情况中都能删掉的部分,即C1(2)和C3(2)。
这些就是外鳍鱼的所有情况了,那么,它还能简化吗?请看下一节。


