




盘面26(图6-4)的题目来源于Enjoy Sudoku数独论坛。它的定义域是列2、列3、列7、列8,而删除域则是行A、行B、行D、行G。此处省略其假设情况,请自行推理(四链列的出现频率是极低的,很难碰到,所以我们不再详细讲解,依然利用刚才的假设法得到对应的结论,只不过可能会分3次假设,比较困难)。四链列和三链列的推理方式大同小异。这个就是四链列或水母。此处结论应为:行A、行B、行D、行G中剩余单元格内将删除候选数9。
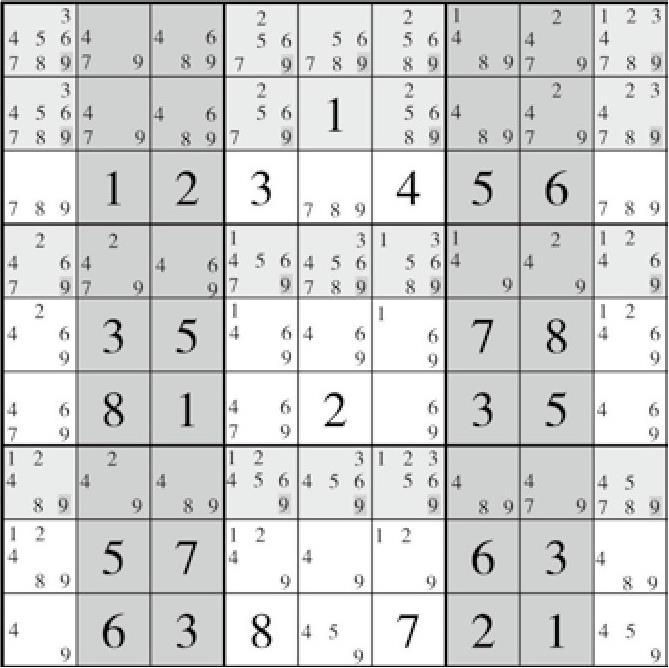
图6-4 盘面26
但是,四链列也同样具有部分单元格残缺的情况,一般来说,残缺的更为常见。如盘面27(图6-5)的这个残缺四链列结构:
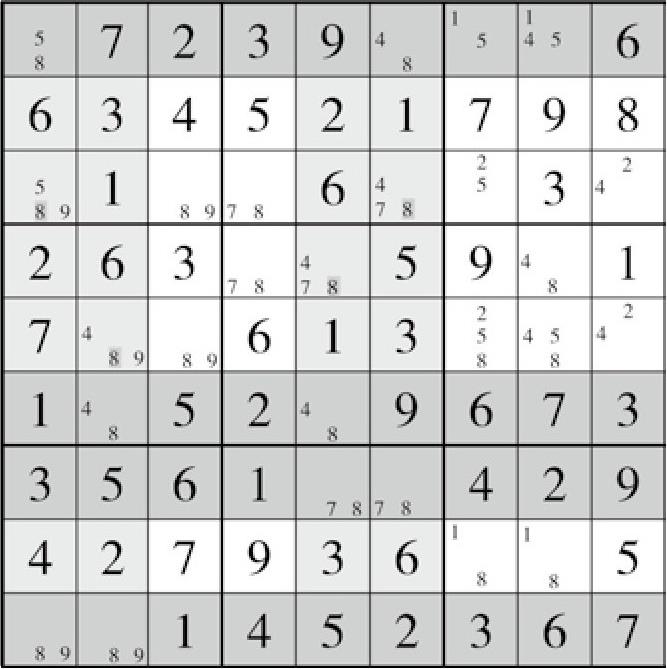
图6-5 盘面27
此处,四链列所涉及的单元格只有8格,但是仍然可以进行推理。不过,它只有两种情况了。
如果A1=8,则I1<>8,则I2=8,F2<>8,则F5=8,G5<>8,则G6=8,A6<>8;反过来也就得到了I1、F2、G5、A6都为8了。但无论是哪种情况,列1、列2、列5、列6内都不得在其余单元格内出现8。因此删掉它们。
高阶链列(高阶鱼)是当阶数大于4后的情况。这样的技巧也同样存在,但是和n>4的数组一样,只存在于理论之上。这是因为高阶链列会被与其垂直的鱼完全替换,原鱼和可用于替换的鱼的阶数和盘面尺寸有关,最高的是阶数与9互补的情况。
根据上述文字可列出下表(表6-2),从中就可了解到高阶链列的一些详细情况了:
表6-2 高阶链列与鱼的相互替代

从上表中我们也能够看出,为什么不存在八链列的说法。
下面的盘面28(图6-6)将展示五链列的其中一个例子。数字1加叉号为被删除情况,数字1加圆圈为五链列,它也属于残缺的情况。不过,它可以转化成一个关于候选数1的三链列。
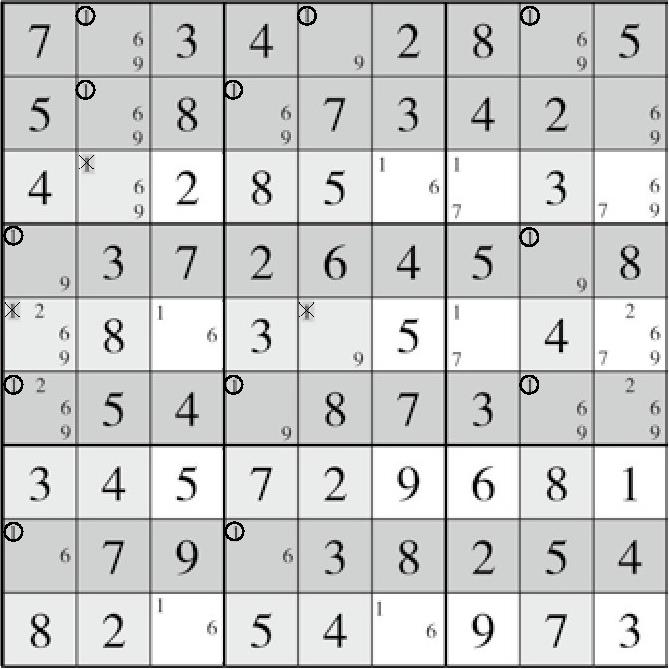
图6-6 盘面28