




三链列比起二链列的情况会多一些,因为它需要更多的假设和推理,如盘面24(图6-2)所示:

图6-2 盘面24
此时我们观察到,在行C、行F和行H都有且仅有列标为5、6、7的单元格可以填4,所以,4在这3行里被控制在那9个单元格内。这时候就假设一下:
●情况1:如果C5=4,则F5、H5、C6、C7都不等于4,解不出,就继续假设:
A.如果F6=4,则F7、H6都不等于4,则H7=4;
B.如果F7=4,则F6、H7都不等于4,则H6=4。
●情况2:如果C6=4,则C5、C7、F6、H6都不等于4,解不出,就继续假设:
A.如果F5=4,则F7、H5都不等于4,则H7=4;
B.如果F7=4,则F5、H7都不等于4,则H5=4。
●情况3:如果C7=4,则C5、C6、F7、H7都不等于4,解不出,就继续假设:
A.如果F5=4、则F6、H5都不等于4,则H6=4;
B.如果F6=4、则F5、H6都不等于4,则H5=4。
此时,我们发现,假设情况均列出了。由于第一次假设并不能完成推理,因此中途又进行了第二次假设,才完成了整个推理过程。对比这6种情况假设的开头以及结尾,可列出下表(表6-1):
表6-1 三链列推理
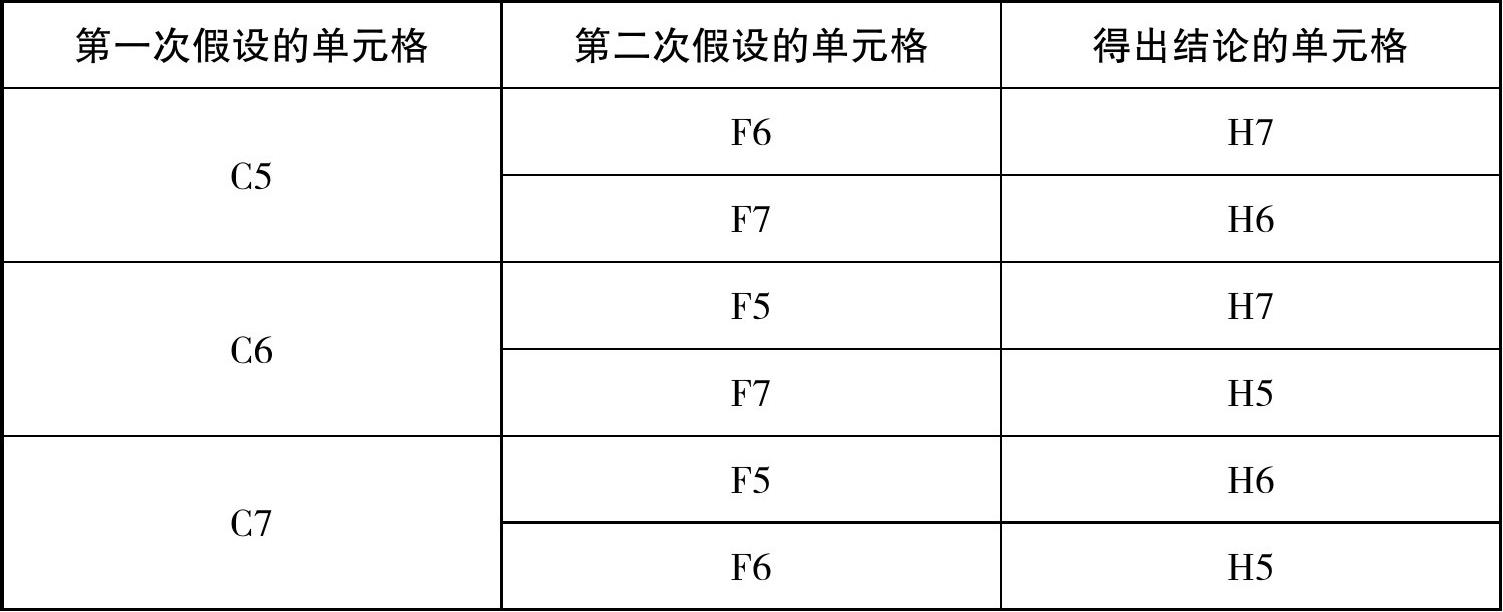
我们发现,无论是哪种情况的假设,始终都会使得列5、列6和列7上至少都有一个4。也因此,列5、列6、列7的其他位置上,候选数4将可以被安全地删掉,亦即图上的A5、A6、B5、B7、D5、D7、G5内的候选数4均将被删除。这就是三链列或剑鱼。注意,此题的三链列的定义域为行C、行F、行H,删除域为列5、列6和列7。
但是,图中有一个奇怪的地方。图上有一个宫摒除法的例子,由B6(8)、G1(8)和I8(8)在宫8内摒除得到H5=8。填入了这个8之后,就会发现一大堆可由摒除法得到的填数,还有两个可以通过唯一余数法得到的填数,于是就一口气做到了这里,如盘面25(图6-3)所示:
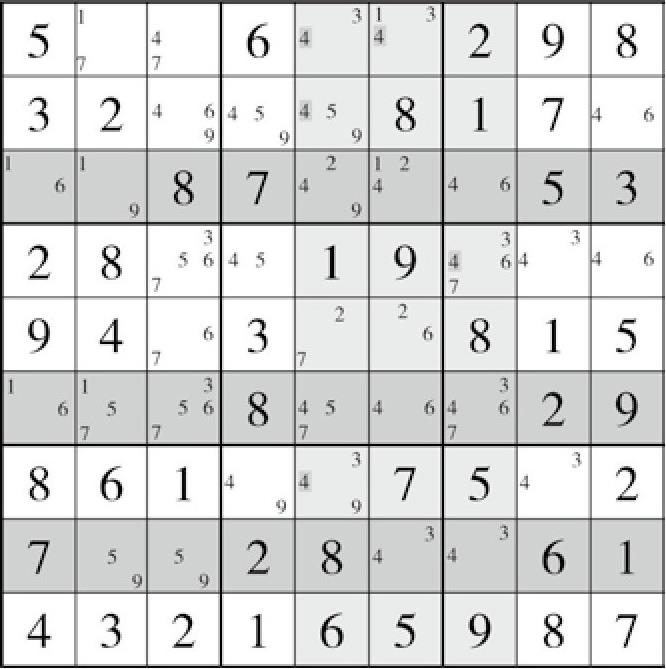
图6-3 盘面25
原来的三链列残缺成了这样(缺了一个“角”),那么它是否还可用呢?答案是肯定的。这并不影响三链列的用法。需要做出的假设会变少,但是仍能推理,并且把所有假设集合在一起,同样可以使得列5、列6、列7都至少有一个4出现。此处将不再列举其假设。这种情况被称为鱼的残缺。我们可以把它想象成一个“二维”的数组,填数情况已经列举到这样的3行、3列之中,相当于一个三链数涉及的3格内的填数情况,第1格是{123},第2格是{123},而第3格则是{12}。数组的要求是满足每一格不一致,所以只需要至少每格2个候选数,就可以构成数组了。