
下载掌阅APP,畅读海量书库
立即打开




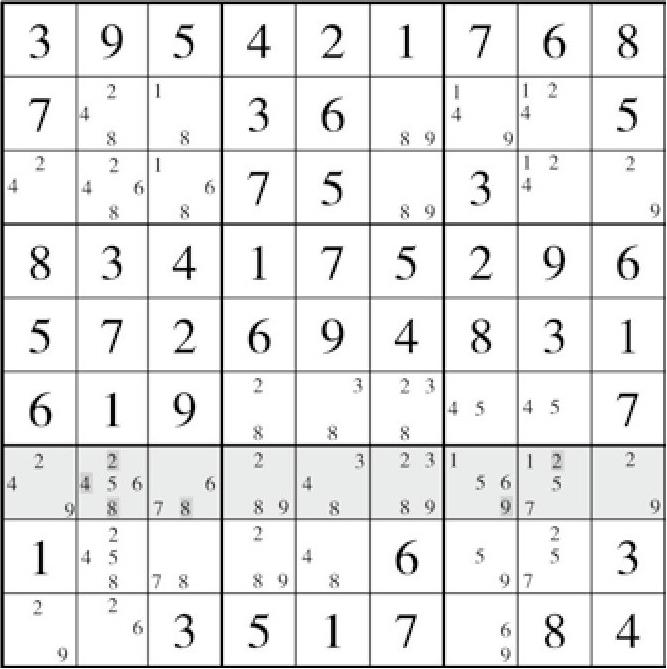
图5-3 盘面22
如盘面22(图5-3)所示,行G暂时没有填入一个数字。此时观察到,G1的候选数{1567}会被列1的B1(7)、E1(5)、F1(6)、H1(1)摒除;而G4、G5、G6这3格会被列4、5、6里面的提示数1、5、6、7摒除;另外列9的1、5、6、7也会摒除掉G9的{1567}。此时行G就只有4个单元格可以填入1、5、6、7了(分别是G2、G3、G7和G8)。所以G2、G3、G7和G8内的其余填数情况均可被删除,即G2、G3、G7、G8的候选数都为{1567}。
这个就是四链数占位法。
至此,数组的内容就结束了。但是您需要注意以下内容:
4<n<9的数组(如五链数、六链数等)也是同样存在的。但是,根据简单的知识,就可以证明得到一个结论:显性数组的存在必然会导致隐性数组的出现,两者是互补的。这里就不再证明了,只需要记住即可。
举个例子,假如在行E中,有一个四链数唯余法,那么不难发现,就这一行而言,它就可以被一个三链数占位法完全代替。所以4<n<9的数组一般都只是理论上存在而实际上并不存在的。一般来说,本书里面不强调互补关系的时候,称为唯余法和占位法方便理解;而涉及两种数组的对比时,会使用显隐性数组的说法,这样方便区分。