
下载掌阅APP,畅读海量书库
立即打开




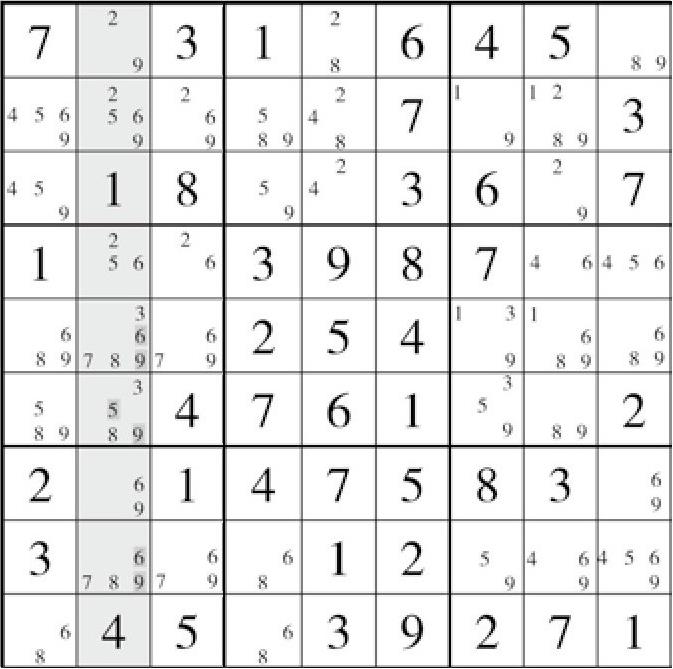
图5-2 盘面21
如盘面21(图5-2)所示。能够观察到,在列2,数字3、7和8只能出现在E2、F2和H2。此时观察到,在同一列内只有3个格子可以填入这3种不同的数字,这依然满足数组的定义,它们可以构成三链数结构。因此,E2、F2和H2这3格内的其他填数情况将被全部删除。因此,E2<>{69}、F2<>{59}、H2<>{69}。
快速观察到数组占位法的最简单方式是观察提示数。例如:在此题中,我们能够观察到的就是列2里面,宫1内的提示数3、7和8会排除掉A2和B2的候选数{378};而D2(3,7,8)被D4(3)、D6(8)以及D7(7)排除了;而G2(3,7,8)也被G8(3)、G5(7)和G7(8)排除了。这个时候,3、7、8这3个数字就只剩下E2、F2和H2这3个位置可以填了。因此这满足三链数结构,当然这个三链数结构内部的其他数字就能删掉了。
又如盘面20,宫4内的D3和F3是我们最终可以得到结论的单元格,因为宫4内的其余单元格并不可能含有数字7和9,它们都被其周围的提示数以及填入的7和9排除掉了。


