
下载掌阅APP,畅读海量书库
立即打开




如盘面18(图4-3)所示。在列2里,D2={578}、G2={578}、I2={578}。
根据数组的定义,同在一个单元内出现n个单元格内存在n种不同数字,它们就能组成一个数组。我们很容易地发现,此时恰好满足n=3的情况。根据数对唯余法类比推理,候选数为{578}的情况在列2中应当只存在于D2、G2和I2,所以可以删除列2内剩余单元格的候选数{578}。
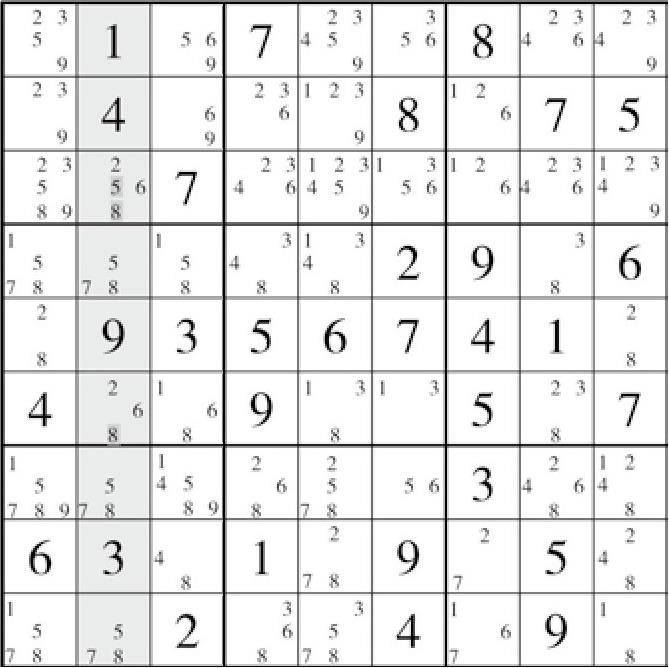
图4-3 盘面18
当满足数组定义中n=3的情况时,我们称这样的数组叫作三链数。另外,也同样存在三数组的说法,它们都是指数组定义的n=3的情况。
数组中的定义仅包含这样一句话,可以认为组成数组的某些格中的候选数可能会缺少一些数字,而所得数组依然成立。以下是一些常见组合情况(以数字1、2、3来说明):
●{123}、{123}、{123};
●{123}、{123}、{12};
●{123}、{12}、{13};
●{12}、{13}、{23}。
这些组合都是成立的,都能构成三链数结构,因为它们都满足数组的定义。并且,最后一种情况是三链数的最简形式。如果再简化,就可以直接得出所填数字了。
另外,如果数组涉及的单元格组同时都属于同一行、列、宫内,这样的数组将直接被称为死锁数组。这是因为它属于数组,但由于本质结构的特殊性,还能看成一种特殊的区块,使得删数成立。