




区块排除法是特殊的排除法,它和之前的排除法有些许的不同。它分为两种。
如盘面10(图2-5)所示。我们发现在宫2中,数字4的位置无论是在A5还是A6,都恰好在行A。但是无论怎么说,这两个位置都必须有一个数字填入4,因此行A的其余位置都不能填4。D9和F9同理。此时我们发现,宫3只有C8可以填4,所以C8=4。
这种技巧被称为区块排除法,而盘面11(图2-6)这个例子则为另外一种区块排除方法,只是推理过程稍微反了一下。
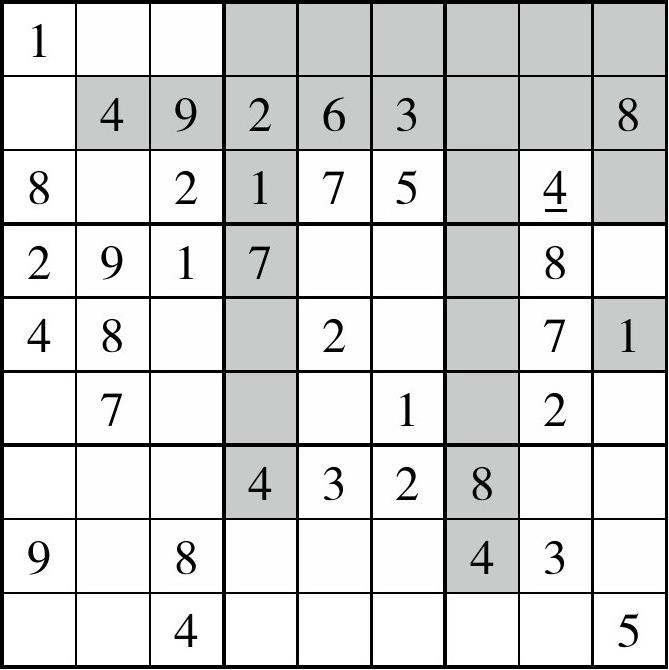
图2-5 盘面10
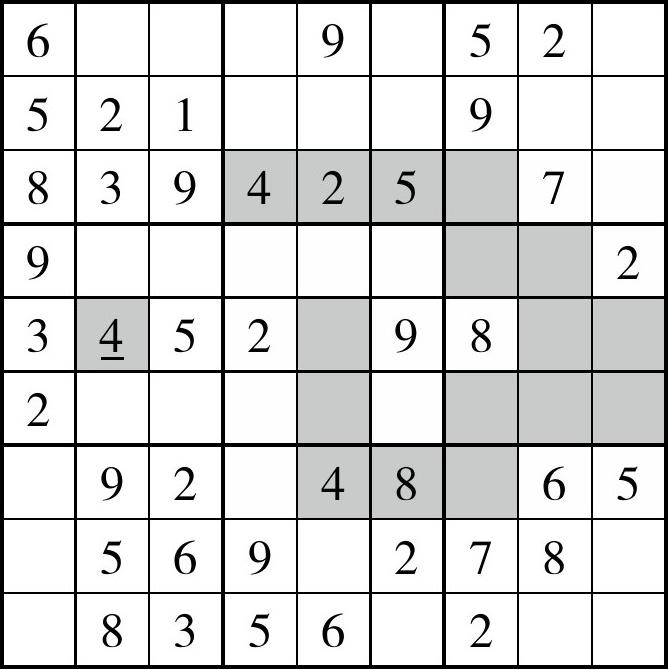
图2-6 盘面11
如盘面11所示。我们观察到,在列7上,填4的位置只剩下了D7和F7这两个单元格。但是不管哪一个是4,我们始终能够发现的是,这一宫(宫6)内,其余位置都不能再填入4。那么观察行E,我们发现,最终行E能够填入4的只有一个位置——E2。因此,E2=4。
在做题过程中,可以采用图中的这种涂色的方式来看,不过这里由于是区块排除法,所以有些地方不一定很直观,就需要自己在做题过程中进行锻炼,才能很快看到它们。
如盘面12(图2-7)所示,根据盘面所给出的提示数,普通的排除法和区块排除法已经无法帮助我们找到可填的数字了。这个时候我们观察I9。
I9的相关格组分别在行I、列9和宫9,于是就看这三个单元,我们发现一共出现了1、2、3、4、5、6、7、9这些数字。根据摒除法的规则,I9的位置将不得填入它们。神奇的是,在9个数字中,只有8没出现。根据“1~9的每个数字都要出现一次”的法则,得到结论,I9=8。

图2-7 盘面12
以上所用的方法就是唯一余数法,简称唯余法,是一种某个单元格中被摒除法排除情况后,只剩下1~9中的某个数字没有填,从而得到它就是此单元格的值的解法。唯一余数法也可以适用于仅在同一个单元内部的推理,中文称为点算。
当全盘具有候选数的时候,唯余法将变得很好观察:某一个单元格内只有1个候选数的时候,它就是这个单元格的值,这就是唯余法。