




1.实际性原则
课题的设计,应该取自于学生周围环境中的实际问题,使学生懂得只要细心地观察周围世界,就能发现处处都是数学,数学原理是那么贴近生活,从而激发他们通过在现实中的应用来理解数学概念,进而解决现实世界中发现的问题。如研究性课题1:调查市场上各种饮料罐(易拉罐)的形状及大小,并用数学知识说明设计的合理性。研究性课题2:某初级中学有200名学生,其中初一年级有100名,初二年级有60名,初三年级有40名,选21名学生发放奖金,如何分配名额才合理?
2.创造性原则
数学研究性课题的设计要着眼于学生创造能力的培养。设计的课题一般不要直接给出结论,让学生自己发现问题,提出问题,解决问题,去观察、分析、概括、提炼,不断取得创新成果。如研究性课题3:在一个矩形地块上,欲劈出一部分作为花坛,要使花坛的面积为矩形面积的一半,请给出设计。
3.以学生为主的原则
在研究性学习教学中,教师只是选择活动素材,设计教学过程,鼓励学生从事数学活动的课堂的组织者、引导者、合作者、共同研究者。学生才是研究性学习舞台上的主角。他们的活动主要是讨论、探索与交流,研究性学习课堂上始终洋溢着民主、活跃的气氛,学生因不同见解而引发激烈的争论,在争论中,他们提出、说明和维护各自的观点,倾听、理解、支持或反驳别人的意见。
数学研究性学习的过程是围绕一个需要解决的数学问题而展开的,它要经过从学生直接参与研究到最终问题解决才结束。其课题可分成课堂内外两种研究性学习课题。根据目前我们学校教学的实际情况,我认为应着重考虑课堂内的研究性学习课题设计,其次考虑课外的研究性学习课题设计。因为数学研究性学习课题,完全可以源于教材,根植于教材。根据教材内容和生活实际可以通过如下途径进行提炼和设计。
1.性质的挖掘
很多数学概念中都具有丰富的内涵,可以设计成研究性学习的课题,让学生自主参与发掘、探索,既使学生熟悉研究数学问题的某些方法,又使学生达到理解掌握知识的目的。如研究性课题4:研究奇(偶)函数 的有关性质涉及的问题有:定义域的对称性;图像的对称性;在原点的函数值;单调性;由奇(偶)函数构成的复合函数的奇(偶)性;由奇偶函数通过四则运算得到的函数的奇偶性等。这些问题可以由学生挖掘、探索和解决。
2.边缘的拓展
高中数学教材因受众多因素的限制,对知识的阐述有的只是局部的特殊的,有的是不完整的,可以进行推广深化和拓展。因而可设计成研究性学习的课题让学生进行探究。如研究性学习课题5:棱(圆)柱、锥、台截侧面积公式:
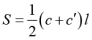 或
或
 。
。
其中
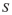 ,
,

 ,
,
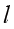 分别为棱(圆)柱、锥台为侧面面积,上下底面周长,半径,母线。当
分别为棱(圆)柱、锥台为侧面面积,上下底面周长,半径,母线。当
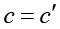 时,台体变为柱体,当
时,台体变为柱体,当
 时,台体变为锥体。即S
棱(圆)柱侧
=cl
时,台体变为锥体。即S
棱(圆)柱侧
=cl
 S
棱(圆)台侧
=
S
棱(圆)台侧
=
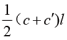
 S
棱(圆)锥侧
=
S
棱(圆)锥侧
=
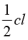 ;或者S
柱侧
;或者S
柱侧
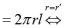 S
台侧
S
台侧
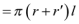
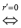 S
锥侧
S
锥侧
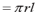 。同理可猜测棱(圆)台、柱、锥体体积之间内在联系:V
柱体
。同理可猜测棱(圆)台、柱、锥体体积之间内在联系:V
柱体
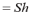
 V
台体
V
台体
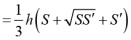
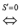 V
锥体
V
锥体
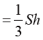 ,其中
,其中
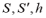 分别为柱台体的上下底面面积和高。当底面半径分别为
分别为柱台体的上下底面面积和高。当底面半径分别为
 ,高为
,高为
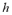 时,
时,
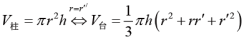
 V
锥
V
锥
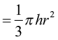 。由此可设计此研究性学习课题。让学生探索、研究、深化、拓展、证明得出结论。
。由此可设计此研究性学习课题。让学生探索、研究、深化、拓展、证明得出结论。
3.开放性
数学开放性题能有效地激发学生的探求兴趣,也能培养训练学生的各种思维能力和思维品质。数学开放性题也接近真正的数学问题的研究,因而数学开放性题就是好的研究性学习的课题。
如研究性学习课题6:设
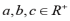 ,且
,且
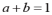 ,试问
,试问
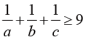 是否成立,并猜想研究其他与
是否成立,并猜想研究其他与
 有关的不等式,结论有:(1)
有关的不等式,结论有:(1)
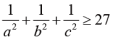 ,(2)
,(2)
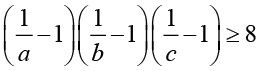 ,(3)
,(3)
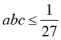 ,(4)
,(4)
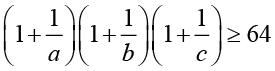 ,(5)
,(5)
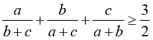 ,(6)
,(6)
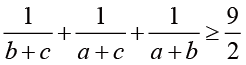 ,(7)
,(7)
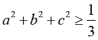 ,(8)
,(8)
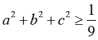 ,(9)
,(9)
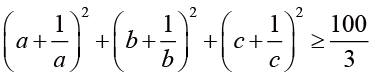 ,(10)
,(10)
 ,(11)
,(11)
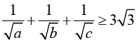 ,(12)
,(12)
 等。上述探究其实就是在保留条件的前提下而深化结论,以原题的已知条件为基本素材,研究在所给条件下的各种可能情形,培养和训练学生的联想,构造,变形研究能力,给学生广阔的思考空间,激发探究欲,的确是一种好的途径。
等。上述探究其实就是在保留条件的前提下而深化结论,以原题的已知条件为基本素材,研究在所给条件下的各种可能情形,培养和训练学生的联想,构造,变形研究能力,给学生广阔的思考空间,激发探究欲,的确是一种好的途径。
4.建模应用
数学建模无疑是研究性学习的重要形式,通过数学建模,培养学生利用数学知识解决实际问题的能力,掌握研究解决实际问题的思想方法,感受数学与生活生产实际的密切联系,进而鼓励学生学习数学应用数学的积极性。建模应用课题可以从以下几个方面入手。
(1)可以在研究性学习课题上留出让学生自己补充、收集信息的余地,使学生能够自己收集有关信息,并进行选择。
如研究性学习课题7:某家具厂有方木90立方米,五合板600平方米,准备加工成书桌和书橱出售,已知生产每张书桌需要0.1立方米,五合板2平方米,生产书橱需方木0.2立方米,五合板1平方米,如何安排生产可获得利润最大。在传统观念下此问题是无法解的,是信息数据不全的问题,现在需学生去收集书桌和书橱的价格信息,再挑选最便宜和最贵的价格,然后利用数学方法计算出利润。
(2)可将研究性学习课题不设问,只叙述或呈现信息,让学生自己提出问题。
如研究性学习课题8:甲,乙,丙三位学生在学期的三次数学测试中成绩如下表:
2015年秋季学期期中数学测试学生成绩表
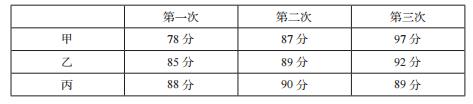
学生可按照不同的角度进行设问如:平均成绩谁最高?谁进步最大?谁的成绩最稳定等问题。
(3)对日常生活和其他学科中出现的问题,从数学的角度进行研究,设计成研究性学习课题。使学生学会收集整理第一手资料,提出问题,建立数学模型,问题求解,模型检验及应用。
如研究性学习课题9:分期付款中的有关计算问题、如何存款才获得最大利润问题等等。让学生收集有关利率值、利息计算方法,提出问题,建立数学模型,求解此模型,最后将此方法或用计算机高级语言编写程序而应用于生活实际中并检验其模型的正确性。如研究性学习课题10:(四腿椅子稳定模型)有四条腿的桌椅往往不能一次放稳(四条腿都着地),有时需要在一条腿上垫一块垫片才能放稳。因此细心的人会提出:在凹凸不平的地面上,一把椅子的四条腿是否可以同时着地?
数学研究性学习开展,需要我们教师的指导,设计研究性学习课题是关键。只要我们在教学过程中,多留心,多指导。会设计出很多优秀的高中数学研究性学习课题。