




在如图2-21(a)所示的理想NMOS器件中,当栅源电压 V GS 从0V开始上升到一定值时,栅极下面的P型衬底中的空穴将被驱走,不能移动的带负电荷的受主离子与栅极上的正电荷形成电场 E 。根据第2.2节中的讨论,此时由多晶硅栅、栅氧化层和P型衬底构成的MIS结构处于多子耗尽状态,NMOS器件的能带图如图2-21(b)所示。
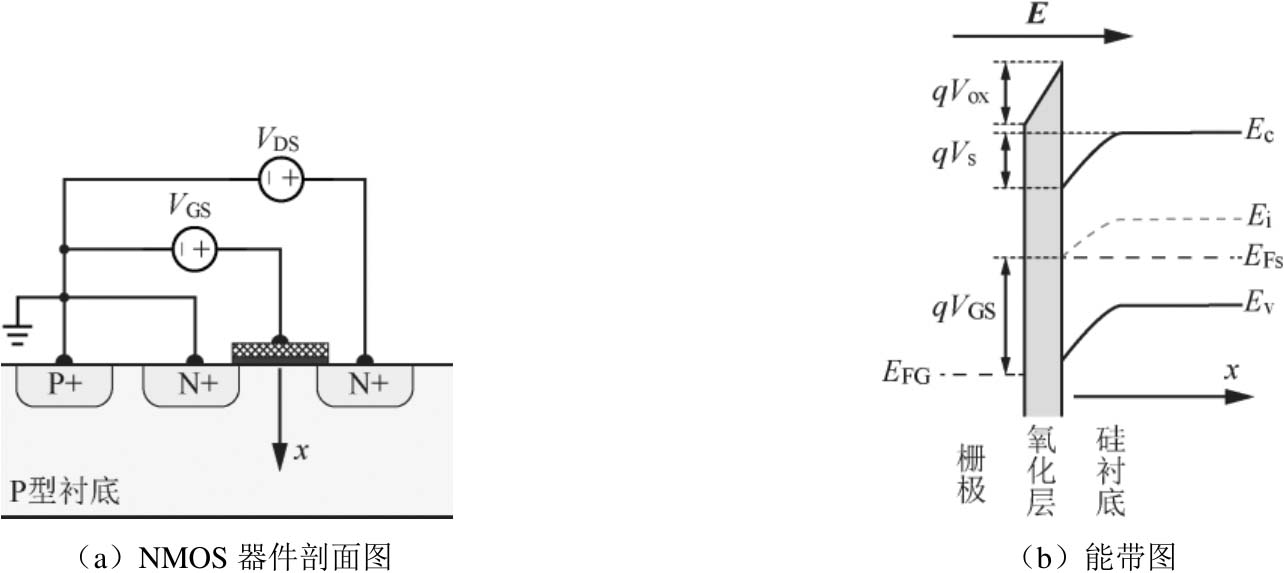
图2-21 分析NMOS器件处于多子耗尽状态时的 V GS 电压
接下来分析当 V GS 为多大时,NMOS器件会进入多子耗尽状态。以硅衬底表面作为原点,栅极指向衬底的方向为 x 轴正方向,则 V GS 所形成的电场 E 的方向为 x 轴正方向。由能带图可知, V GS 所形成的电场一部分作用在栅氧化层上,另一部分作用在硅衬底表面。电场的方向是电势降低的方向,因此对于电子来说,沿着 x 轴正方向附加电势能升高,所以表面处的能带会低于体内的能带;对于栅氧化层来说,其能带弯曲大小为 qV ox ;对于硅衬底表面来说,其能带弯曲大小为 qV s 。 V ox 和 V s 分别是 V GS 落在栅氧化层和硅衬底表面上的电势, V s 也被称为半导体的表面势,因此有 V GS = V ox + V s 。在图2-21(b)中, E FG 和 E Fs 分别是栅极和硅衬底的费米能级,可知在 V GS 作用下, E FG 比 E Fs 低 qV GS 。要想分析多子耗尽状态下的 V GS ,就要分析该状态下的 V ox 和 V s 。在多子耗尽状态下,硅衬底表面形成电离受主构成的耗尽层,其厚度记为 x d ,在 x d 处电场 E 的大小降为0,硅衬底表面处的电势和电场分布如图2-22所示。
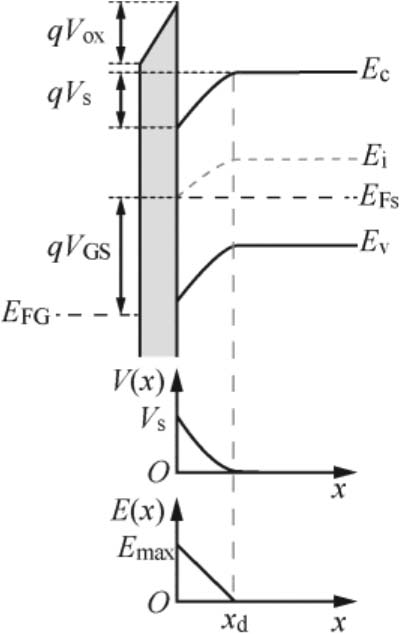
图2-22 硅衬底表面处的电势和电场分布
通过分析耗尽层中的电荷量以及栅氧化层所形成的电容便可得到
V
ox
。假设P型衬底的掺杂浓度为
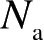 ,使用一维分析,则耗尽层的电荷密度
ρ
可表示为
,使用一维分析,则耗尽层的电荷密度
ρ
可表示为
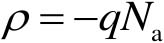
(2-10)
根据泊松方程,可得到耗尽层中电势 V ( x )的微分方程
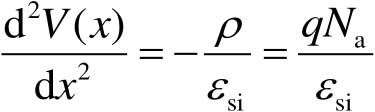
(2-11)
式中, ε si 为硅的介电常数。对式(2-11)进行积分即可得到耗尽层中的电场强度
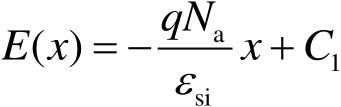
(2-12)
式中, C 1 为积分常数。根据电场强度的边界条件 E ( x d )=0,可以计算得到 C 1 为
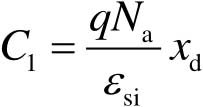
(2-13)
因此得到耗尽层中电场强度 E ( x )的表达式为
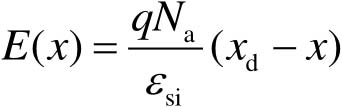
(2-14)
根据电势和电场强度的关系可得
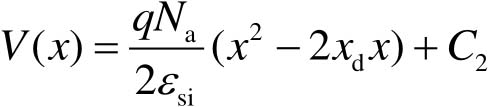
(2-15)
式中, C 2 为积分常数。根据电势的边界条件 V ( x d )=0,可以计算得到 C 2 为
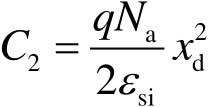
(2-16)
因此得到耗尽层中电势 V ( x )的表达式为
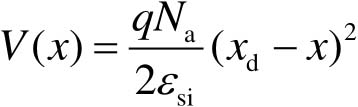
(2-17)
根据电势的另一个边界条件 V (0)= V s ,可以计算得到耗尽层宽度 x d 为
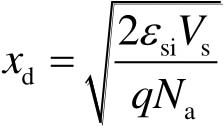
(2-18)
根据式(2-10)所示的耗尽层的电荷密度,可得到单位面积耗尽层的电荷量为
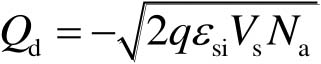
(2-19)
考虑MIS结构的电容特性,栅氧化层类似电容的介质层,其厚度记为 t ox ,其介电常数记为 ε ox ,因此单位面积栅氧化层电容 C ox 可表示为
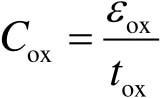
(2-20)
因为栅氧化层电容上所存储的电荷量为| Q d |,因此 V ox 为
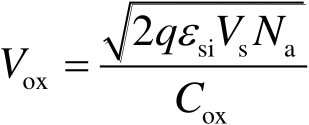
(2-21)
因此耗尽状态的 V GS 可表示为
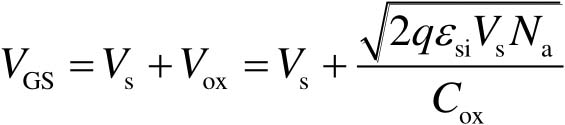
(2-22)
接下来分析当 V GS 继续增大到多大时,栅下会出现反型,形成N型导电沟道,此时的 V GS 为NMOS器件的开启电压,即阈值电压 V TH 。通过式(2-22)发现, V GS 是 V s 的函数,因此只要知道反型时 V s 的大小,便可求得 V TH 。对于NMOS器件来说,栅下出现反型的重要标志是反型层电子浓度等于衬底体内的空穴浓度。反型状态下NMOS器件的能带图如图 2-23所示,当半导体表面处 E Fs 高出禁带中线 E i 的距离刚好等于半导体体内 E Fs 低于禁带中线的距离 qΦ F 时,表面处电子浓度等于体内的空穴浓度,此时 V s =2 Φ F 。
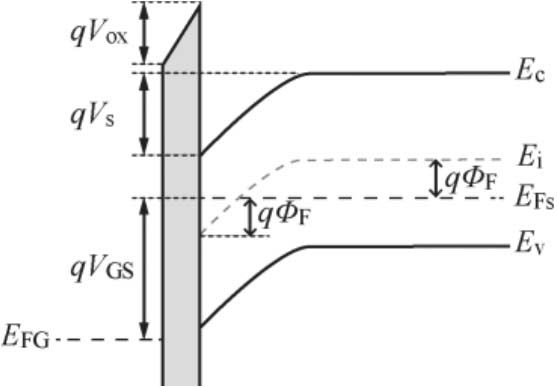
图2-23 反型状态下NMOS器件的能带图
对于P型半导体,空穴浓度 p 0 = N a ,因此有
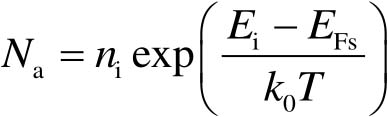
(2-23)
式中, n i 为本征载流子浓度。考虑 qΦ F = E i - E Fs ,则可得到 Φ F 为
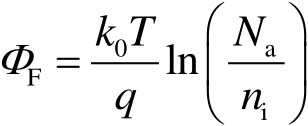
(2-24)
因此得到NMOS器件的阈值电压 V TH 为
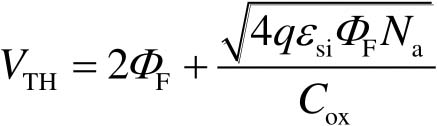
(2-25)
上述分析中考虑的是理想NMOS器件,即当 V GS =0V时半导体处于平带状态。但实际上栅极材料和衬底材料之间存在功函数差和表面缺陷,且栅极氧化层中可能存在电荷,考虑这些因素后,当 V GS =0V时,半导体并不处于平带状态。我们对 V TH 的分析是在平带状态基础上开展的,因此当考虑上述非理想因素后,需要对式(2-25)所示的 V TH 加上平带电压修正项 Φ FB , V TH 修正为
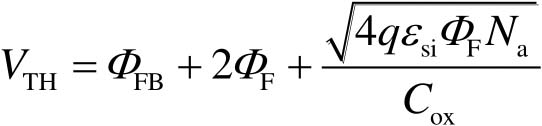
(2-26)
阈值电压的表达式可以分解成三部分。其中 Φ FB 将能带恢复为平带状态;2 Φ F 将作用在半导体表面使半导体出现反型;最后一项是栅氧化层两端的电压差,即栅极上为了镜像耗尽层中电荷 Q d 而要施加的电压。前面的分析假设源极和衬底均连接到0V电位上,但在实际应用中,NMOS器件的源极电压可能会高于0V,源极电压高于衬底电压的NMOS器件如图2-24所示。
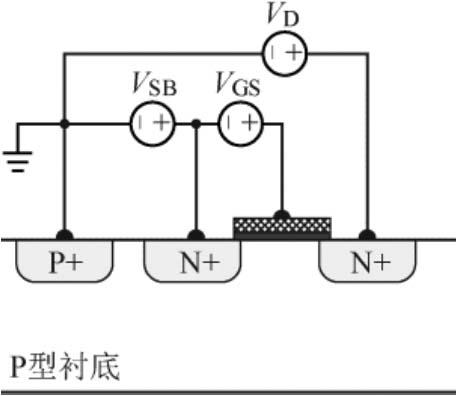
图2-24 源极电压高于衬底电压的NMOS器件
当 V GS 略小于 V TH 时,栅下出现耗尽层但还未反型,由于 V SB >0,使得耗尽层宽度增加。因此需要更大的 V GS 以镜像耗尽层中的电荷,使 V ox 变为
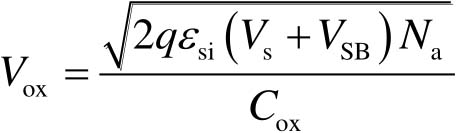
(2-27)
因此阈值电压变为
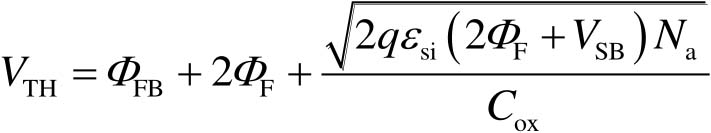
(2-28)
可知,当源极电压比衬底电压更高时,即更大的 V SB ,NMOS器件的 V TH 也变得更大,该现象被称为体效应。定义体效应系数 γ 为
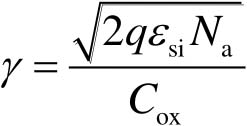
(2-29)
因此考虑体效应后,NMOS器件的 V TH 可表示为
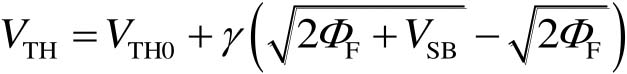
(2-30)
式中, V TH0 为式(2-26)所示的未考虑体效应时的阈值电压。
以上是针对NMOS器件阈值电压的分析,而PMOS器件的导通现象类似NMOS器件的,只是所有极性都是相反的。PMOS器件反型层的形成如图2-25所示,当 V GS 的值足够大时,栅下衬底表面会形成一个由空穴组成的反型层,实现器件源极和漏极的导通。
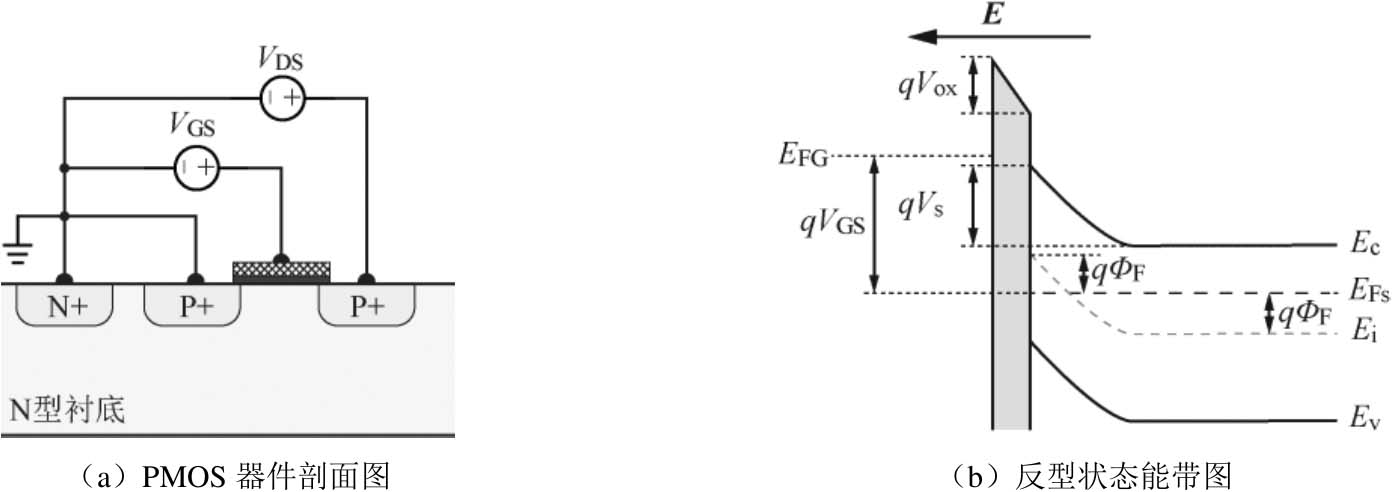
图2-25 PMOS器件反型层的形成
通过前面的分析我们知道,对于NMOS器件,当 V GS ≥ V TH 时栅极下方会形成N型沟道连通源极和漏极,如果在漏极和源极之间施加电压 V DS ,则会形成漏极电流 I D ,可知 I D 是 V GS 和 V DS 的函数,这个函数描述了NMOS器件的 I - V 特性。本节内容将具体分析该函数的表达式。
在分析 I - V 特性之前,我们首先看这样一个例子,假设有一个长方体N型半导体棒,两端施加电压 V ,半导体棒中电子在电场作用下做漂移运动,如图2-26所示,下面分析半导体棒中电流 I 的大小。
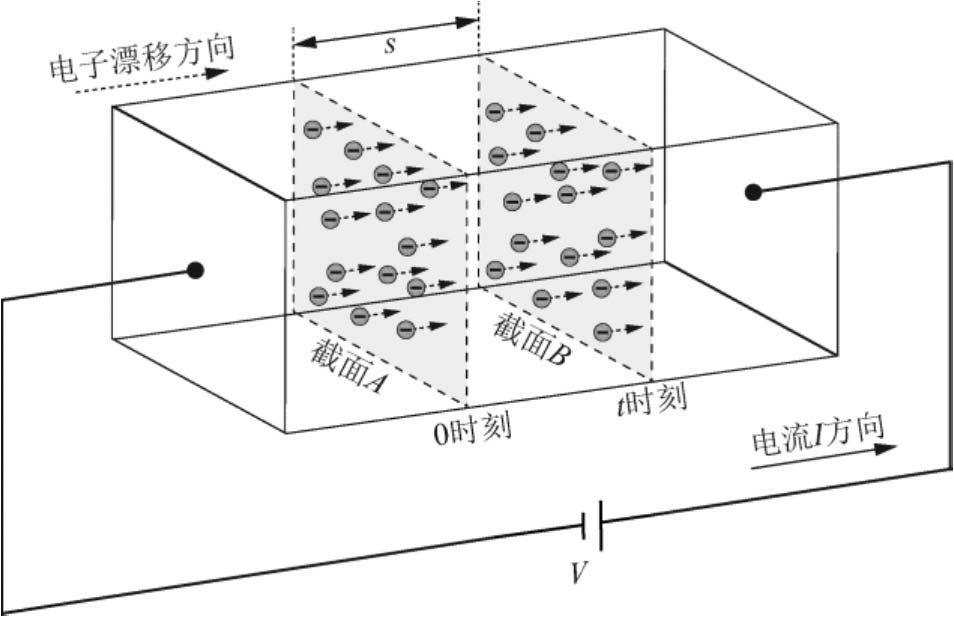
图2-26 长方体N型半导体棒中电子的运动
在该N型半导体棒中,假设0时刻电子运动至截面 A 处,经过 t 时间后运动到截面 B 处,因此在 t 时间内截面 A 和截面 B 之间的电子均通过了截面 A ,即截面 A 和截面 B 之间的电荷全部在 t 时间内通过截面 A 。如果截面 A 和截面 B 之间的电荷量为 Q tot ,根据电流强度定义,则可得到半导体棒中电流 I = Q tot / t 。如果电子的平均漂移速度为 v ,则截面 A 和截面 B 之间的距离 s = vt 。假设该N型半导体棒中沿电流方向单位长度的电荷量为 Q 0 ,则 Q tot = Q 0 vt 。因此可以得到 I = Q 0 v ,这说明半导体棒中的电流大小与其单位长度电荷量和电子平均漂移速度有关。
下面考虑图2-27所示的沟道长度为 L 、宽度为 W 的NMOS器件中的电流大小。其源极接地线,栅源电压为 V GS ,漏源电压为 V DS 。在2.5.1节中我们分析到,当 V GS < V TH 时,栅极下方出现耗尽层,栅极的正电荷被耗尽层中不能移动的电离受主所提供的负电荷镜像。当 V GS ≥ V TH 时,栅极下方出现N型导电沟道,此时栅极上相比于多子耗尽状态时多出的正电荷将被沟道内的电子镜像,所以单位长度沟道内由可移动的电子贡献的电荷量为
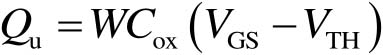
(2-31)
式中, C ox 为栅氧化层单位面积电容,因此 WC ox 表示单位长度电容。沟道中均匀分布电子,类似前面分析的N型半导体棒,其单位长度电荷量即 Q u 。
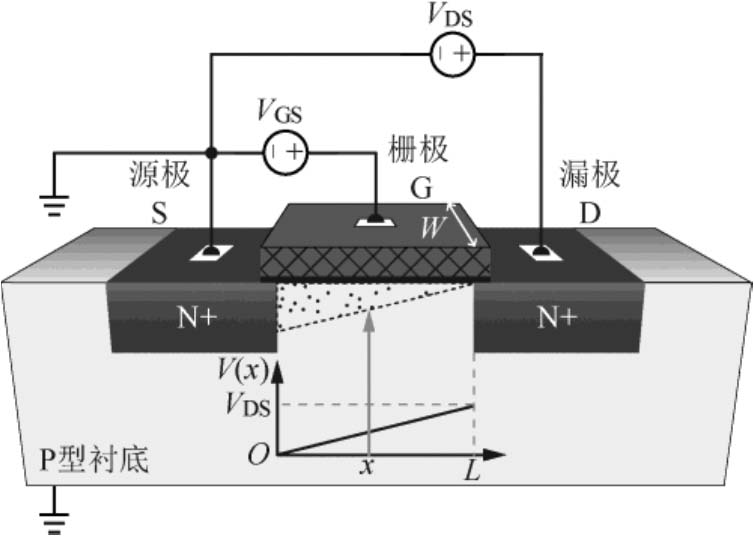
图2-27 NMOS器件沟道中的电流
沟道中的电势从靠近源极一侧的0V线性增加到漏极一侧的 V DS 。将靠近源极一侧的沟道边缘位置定义为坐标原点,以源极指向漏极方向定义为 x 轴正方向,则沟道中的电势 V ( x )是 x 的线性函数,且 V (0)=0, V ( L )= V DS 。因此,沟道 x 点处的单位长度电荷量为
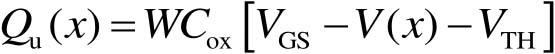
(2-32)
根据对N型半导体棒中电流大小的分析,可以得到沟道中的电流为
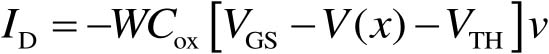
(2-33)
式中,负号是因为沟道内电荷为电子提供而引入的; v 表示沟道中电子的平均漂移速度。根据半导体中载流子迁移率的定义,可以得到 v = μ n E ( x ),其中 μ n 为电子迁移率, E ( x )为沟道内电场强度。再考虑电场强度和电势的关系,可以得到
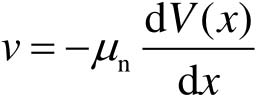
(2-34)
将式(2-34)代入到式(2-33),可得
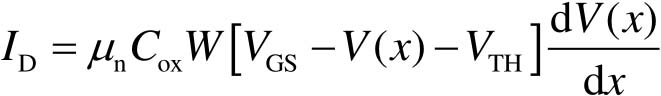
(2-35)
在式(2-35)等号两边均乘以d x ,则等号两边可分别对 x 和 V ( x )进行积分。 x 的积分范围为0~ L ,则 V ( x )与之对应的积分范围为0~ V DS ,因此可得到
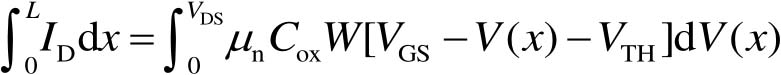
(2-36)
因为 I D 是常数,所以
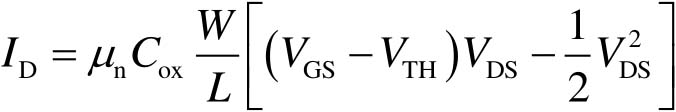
(2-37)
由式(2-37)可看出,在固定的
V
GS
下,
I
D
与
V
DS
呈抛物线关系,且极值发生在
V
DS
=
V
GS
-
V
TH
处,
V
GS
-
V
TH
被称为过驱动电压
V
ov
。当
V
GS
增大时,抛物线整体幅度也增大,这说明NMOS器件的导电能力随着
V
GS
增大而增强。其中
W
/
L
被称为晶体管的宽长比,该值越大,
I
D
越大。在式(2-37)中,如果
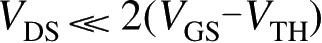 ,则有
,则有
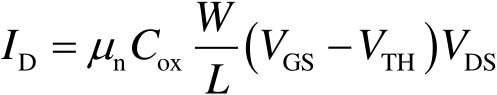
(2-38)
此时, I D 是 V DS 的线性函数,此时NMOS器件的 I - V 特性类似一个压控电阻,其阻值等于
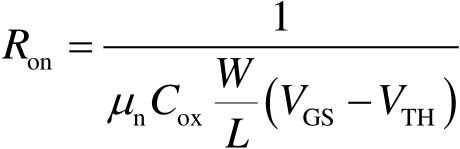
(2-39)
NMOS器件的 I D 符合式(2-37)描述的前提条件是式(2-32)所示的单位长度电荷量 Q u ( x )≥0,这就要求沟道中的电势 V ( x )≤ V ov 。 V ( x )的最大值为 V DS ,因此当 V DS ≤ V ov 时,式(2-37)成立,此时器件工作在线性区。下面分析 V DS > V ov 时 I D 的情况。当 V DS = V ov 时, Q u ( L )=0,即在 L 处沟道刚好消失,此现象被称为沟道夹断,器件工作在饱和区。夹断处不再存在电子,而是处于多子耗尽状态,电阻值相对沟道区域大很多。因此当 V DS 进一步增大时,比 V ov 大出的电压全部落在夹断区域,并使得夹断点向源极移动,有效沟道长度变为 L' ,出现夹断时NMOS器件沟道中的电荷如图2-28所示。
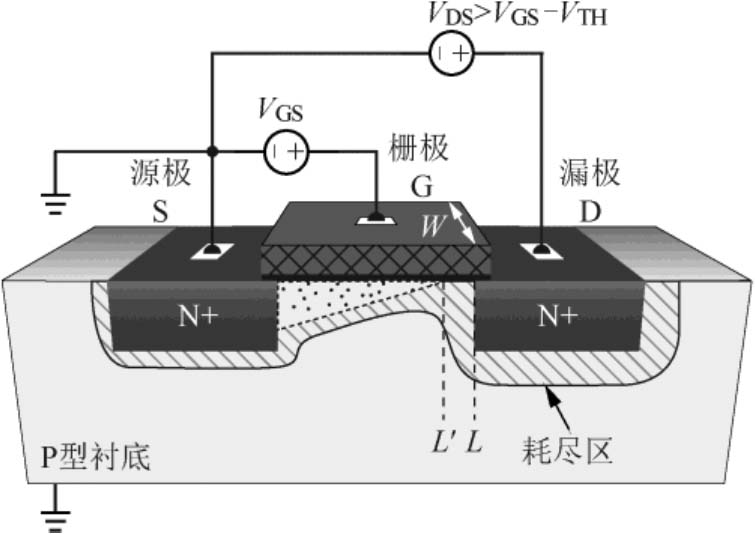
图2-28 出现夹断时NMOS器件沟道中的电荷
在这种情况下,沟道内的电子从源极漂移运动到夹断点后遇到耗尽区,但因为该耗尽区存在一个较强的从漏极指向源极的电场,因此这些运动到 L' 处的电子在该电场作用下快速地被漏极收集。由于该电子收集过程速度很快,几乎不会对电流产生限制,因此器件工作在饱和区时的 I D 是由0到 L' 这段类似半导体棒的沟道区域决定的。所以式(2-36)中等号左边的积分上限变为 L' ,等号右边的积分上限变为 V ov = V GS - V TH ,这样得到
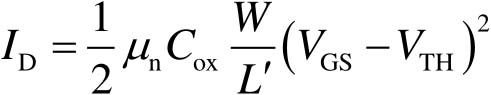
(2-40)
由式(2-40)可知,当 L' ≈ L 时, I D 饱和而与 V DS 无关。此时该器件表现得类似于电流源。但事实上, V DS 增大使得夹断点会靠近源极,这表明 L' 会随着 V DS 的增大而变小,意味着有效沟道长度在变小,该现象被称为沟道长度调制效应。考虑该效应后, L' = L /(1+ λV DS ),因此式(2-40)变为
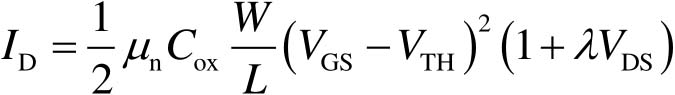
(2-41)
式中, λ 为沟道长度调制系数,该系数越大说明沟道调制效应越明显。由式(2-41)看出,器件工作在饱和区时的 I D 也会随着 V DS 的增大而缓慢增加。这说明在饱和状态下该器件所表现的电流源并不理想,其输出阻抗 r o =(∂ I D /∂ V DS ) -1 ≈( λI D ) -1 ,即 λ 越大输出阻抗越小。
通过上述分析可知,NMOS器件的主要 I - V 特性可由式(2-37)和式(2-41)共同表征,NMOS器件的 I - V 特性曲线如图2-29所示。其中图2-29(a)所示为NMOS器件的输出特性曲线,展现了 I D 与 V DS 的关系,为关于 V GS 的曲线族。当 V GS ≥ V TH ,且 V DS ≤ V GS - V TH 时,器件工作在线性区,位于夹断点轨迹左侧,此时器件表现的特性类似于电阻特性。当 V GS ≥ V TH ,且 V DS > V GS - V TH 时,器件工作在饱和区,位于夹断点轨迹右侧,此时 I D 随 V DS 增大而缓慢增大,器件表现得类似于电流源。

图2-29 NMOS器件的 I - V 特性曲线
当
V
GS
增大时,无论器件工作在线性区还是饱和区,
I
D
均会增大,这说明NMOS器件的导电能力随着
V
GS
增大而增强。器件的
V
GS
调控
I
D
的能力非常重要,可通过图2-29(b)所示的转移特性进行表征。该曲线的斜率表示了器件将栅极与源极之间电压差转换为漏极与源极之间电流的能力,我们称之为跨导,通常用
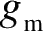 来表示,表达式为
来表示,表达式为
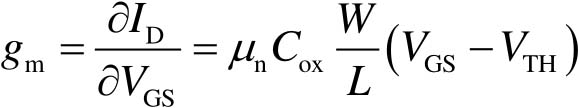
(2-42)
由于过驱动电压 V ov 可表示为
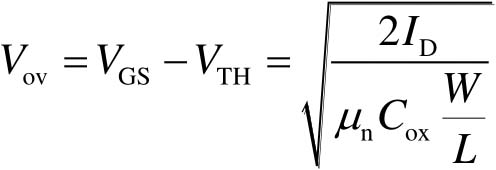
(2-43)
因此结合式(2-42)和式(2-43),
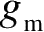 还可以表示为
还可以表示为
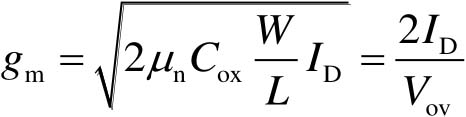
(2-44)
NMOS器件除了线性区和饱和区还有另外两个工作区域,分别是图2-29(a)所示的亚阈值区和截止区,下面讨论这两个区域。当 V GS ≤0时,漏极与源极之间几乎不存在电流,此时器件工作在截止区。而当0< V GS < V TH 时,器件不会完全关断,栅极下方会存在一个较弱的反型层,并存在微弱的漏源电流。此时器件工作在亚阈值区,该状态下器件的 I D 与 V GS 呈指数关系,通常可表示为
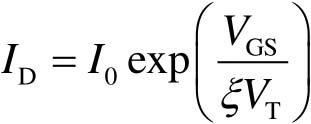
(2-45)
式中, V T = k 0 T / q 为热电压。
最后,我们分析PMOS器件的工作状态。由于PMOS器件的阈值电压极性与NMOS器件相反,因此对于PMOS器件来说,当 V GS ≤ V TH 时器件导通。当 V G - V D > V TH 时,漏极出现沟道夹断情况。所以当 V DS < V GS - V TH 时,器件处于饱和状态。此外,在相同尺寸和偏置条件下,大多数CMOS工艺中PMOS器件的电流要小于NMOS器件的电流。这主要是因为空穴迁移率 μ p 是电子迁移率 μ n 的1/4~1/3,所以PMOS器件的电流驱动能力较低,跨导较小。因此,在电路设计时为保证PMOS器件和NMOS器件具有同样的电流驱动能力,通常PMOS器件的宽长比会设置为NMOS器件宽长比的3~4倍。
MOS器件的栅极与衬底、源极、漏极之间分别存在寄生电容,这些电容会随器件工作状态的改变而改变,对器件的高频特性产生影响。下面以NMOS器件为例,分情况讨论MOS器件电容的情况。
当NMOS器件工作在截止区时,电容情况如图2-30所示。工作在截止区时,器件栅极下方没有沟道,但由于源极和漏极与栅极之间均存在一个交叠电容 C ov ,因此栅极与源极之间的电容 C GS = C ov ,栅极与漏极之间的电容 C GD = C ov 。交叠电容 C ov = WL ov C ox ,其中 L ov 为源极和漏极分别与栅极之间的交叠长度, C ox 为栅氧化层单位面积电容。此外,源极、漏极与衬底之间均形成反偏PN结,因此存在势垒结电容。如图2-30所示,该PN结电容分为底面结电容和侧壁结电容,其中单位面积底面结电容表示为 C j ,单位长度侧壁结电容表示为 C jsw 。因此源极、漏极与衬底之间的电容 C SB 和 C DB ,与源极、漏极区域的面积和周长有关。当源极和漏极的面积分别为 A S 、 A D ,周长分别为 P S 、 P D 时, C SB = A S C j + P S C jsw , C DB = A D C j + P D C jsw 。
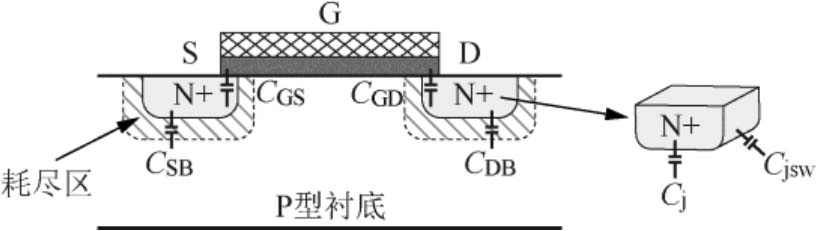
图2-30 NMOS器件工作在截止区的电容情况
当NMOS器件工作在线性区时,其电容情况如图2-31(a)所示。此时,器件栅极下方出现导电沟道且未被夹断,当 V DS 较小时,源极和漏极近似处于对称状态,因此栅极和沟道之间存在的栅氧化层电容被源极、漏极均分。再考虑上源极、漏极与栅极固定存在的交叠电容,则 C GS = C GD =1/2 WLC ox + WL ov C ox 。因为沟道与源极和漏极相连,因此沟道和衬底之间的结电容也被源极、漏极均分,等效增加了源极、漏极区结电容的底面积,所以 C SB =( A S +1/2 A C ) C j + P S C jsw , C DB =( A D +1/2 A C ) C j + P D C jsw ,其中 A C 为沟道底面积。当NMOS器件工作在饱和区时,其电容情况如图2-31(b)所示。此时沟道靠近漏极一侧出现夹断,源极和漏极不再处于对称状态,此时栅极和沟道之间的栅氧化层电容几乎不会贡献给 C GD ,而通常会有大约 2/3 贡献给 C GS 。再考虑上源极、漏极与栅极固定存在的交叠电容,则 C GS =2/3 WLC ox + WL ov C ox , C GD = WL ov C ox 。由于沟道与漏极处出现夹断,因此沟道和衬底之间的结电容也不会贡献给 C DB ,而沟道与源极是相连接的,因此沟道和衬底之间的结电容会全部贡献给 C SB ,则 C SB =( A S + A C ) C j + P S C jsw , C DB = A D C j + P D C jsw 。
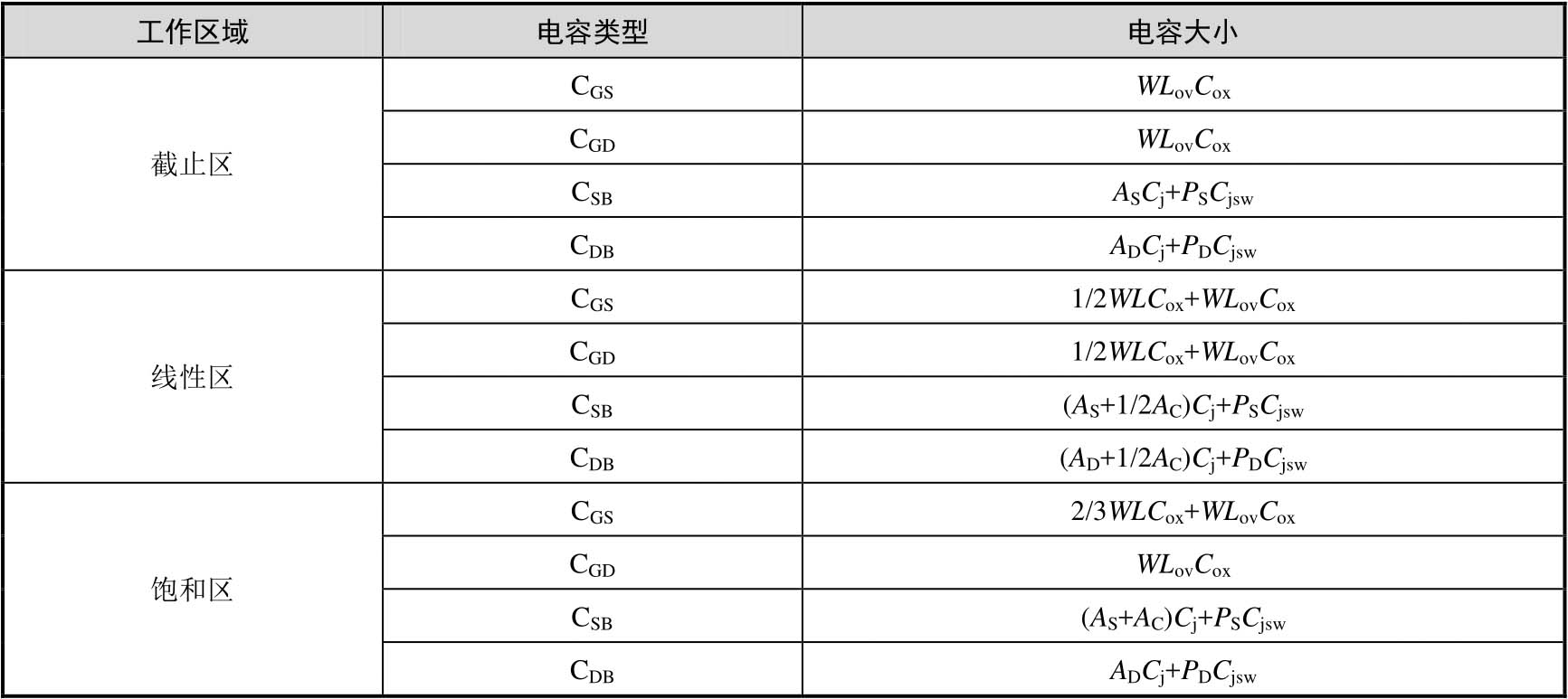
现将NMOS器件工作在不同区域的电容情况进行总结,如表2-2所示。

图2-31 NMOS器件工作在线性区和饱和区的电容情况
表2-2 NMOS器件工作在不同区域的电容情况总结
MOS器件的 I - V 特性是一种大信号模型,利用它我们可以分析确定电路的直流工作状态。当电路的直流工作点确定后,我们往往需要使用小信号模型来分析电路特性。小信号模型是直流工作点附近的大信号模型的近似,是一种有助于简化计算的线性模型,这对于我们计算分析电路特性非常重要。由于在模拟电路中MOS器件主要工作在饱和区,所以这里只讨论饱和状态下的小信号模型。当不考虑器件电容时,MOSFET的小信号模型如图 2-32(a)所示。压控电流源用来模拟 I D 与 V GS 的关系。电阻 r o 用来模拟由沟道长度调制效应引入的非无穷大输出阻抗,它是限制大多数运算放大器最大电压增益的关键因素。当考虑体效应时, V BS 会影响 V TH ,进而影响 I D ,这说明 I D 也是 V BS 的函数。可以通过值为 g mb V BS 的压控电流源来模拟体效应(也称为背栅效应),其中 g mb = ηg m 为背栅跨导, η =∂ V TH /∂ V SB 。在分析交流信号时,我们需要考虑2.5.3节中讨论的器件电容,这样我们就得到了完整的MOSFET小信号模型,如图2-32(b)所示。我们把图2-32所示的小信号模型称为Π型小信号模型或Π模型,用这个模型分析源极接地的电路较为简洁。
常用的MOSFET小信号模型还有另外一种,称为T型小信号模型或T模型,如图 2-33所示。用T模型分析源极非接地的电路相对更简洁。因此我们可以根据两种模型不同的特点,在分析电路时有针对性地选择模型类型。这里需要说明的是,虽然目前计算机仿真均采用更为复杂且精确的器件模型,如BSIM,但Π模型和T模型在人工分析电路特性时仍然非常重要,因此仍需要电路设计人员能够熟练运用小信号模型进行电路分析。
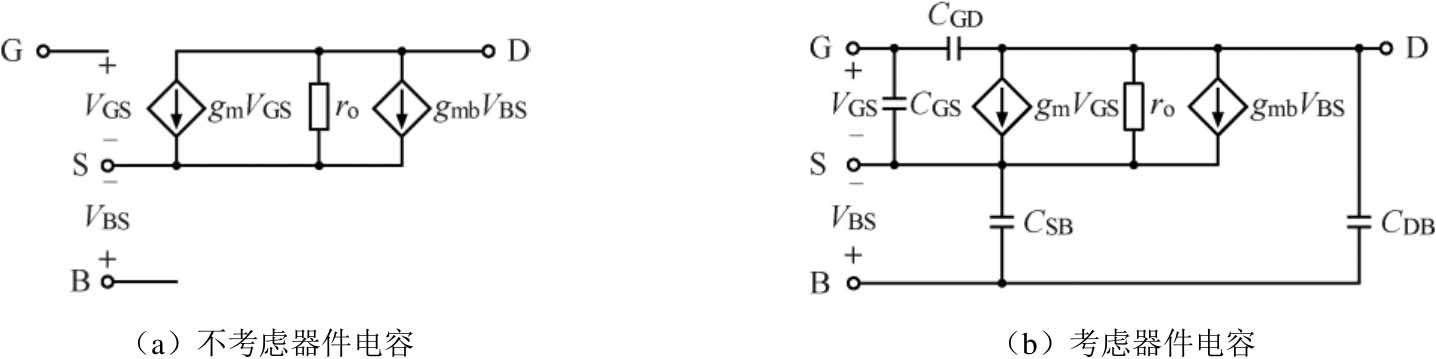
图2-32 MOSFET的Π型小信号模型
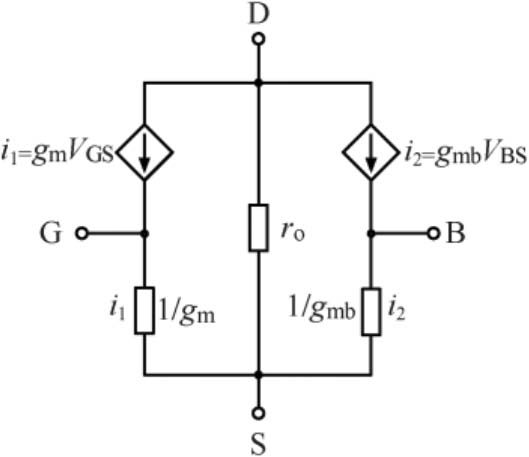
图2-33 MOSFET的T型小信号模型