





1.直线、射线、线段
(1)直线、射线、线段的概念及其区别:
(2)直线公理:经过两点有且只有一条直线。(两点确定一条直线)
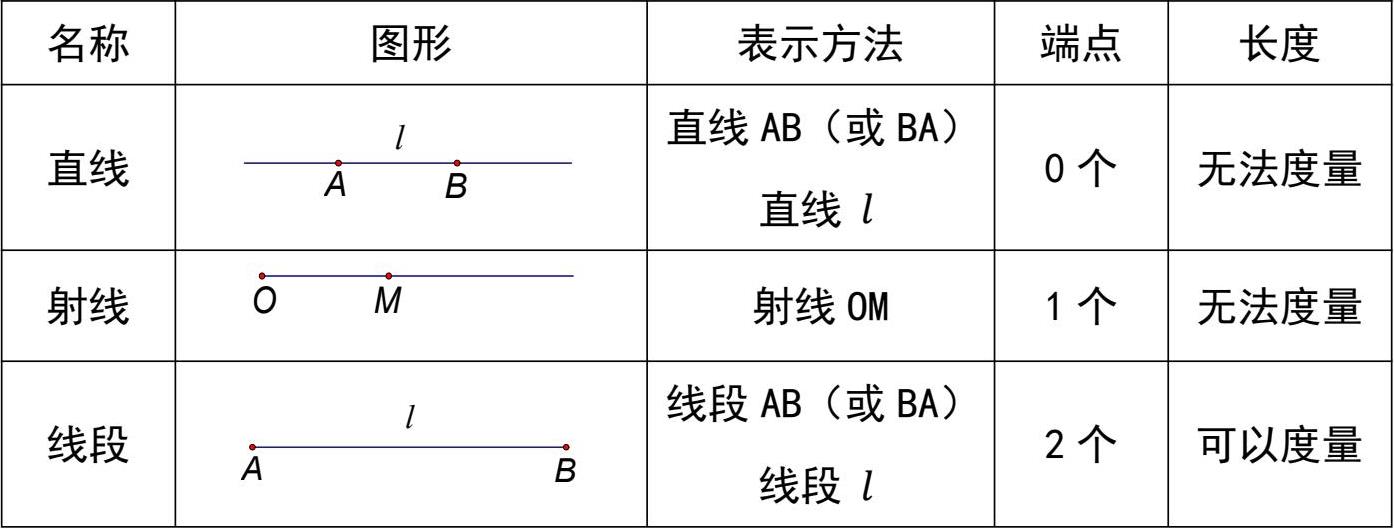
(3)线段公理:两点之间,线段最短。
连接两点所得线段的长度,叫做“两点间的距离”。
2.线段的比较(度量)
①刻度尺度量比较法;②圆规截取比较法。
3.角的定义及表示法:
(1)有公共端点的两条射线组成的图形,叫做角。
(2)由一条射线绕着它的端点旋转而成的图形。(图1-8)

(3)角的表示法:角的符号为“∠”。

4.角的度量
(1)度量方法
①量角器度量法;②重叠比较法。
(2)度量单位:度、分、秒。
度
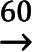 分
分
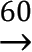 秒,即1º=60';1'=60″。
秒,即1º=60';1'=60″。
(3)度、分、秒的换算

5.平角与周角
(1)一条射线绕它的端点旋转,当终边与始边成一条直线时,所成的角叫做
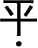
 (如图1-12);(2)终边继续旋转,当它又与始边重合时,所成的角叫做
(如图1-12);(2)终边继续旋转,当它又与始边重合时,所成的角叫做
 (如图1-13)。
(如图1-13)。

■周角>平角>钝角>直角>锐角。
【许子注】平角可以看作一条直线;周角可以看作一条射线。
6.方位角:
(1)基本方向:上北下南,左西右东。(图1-14)
(2)八个方位:东、南、西、北;北偏东(西)、南偏东(西)。
(特殊的,有东北方向、西北方向、东南方向、西南方向。)

图 1-14
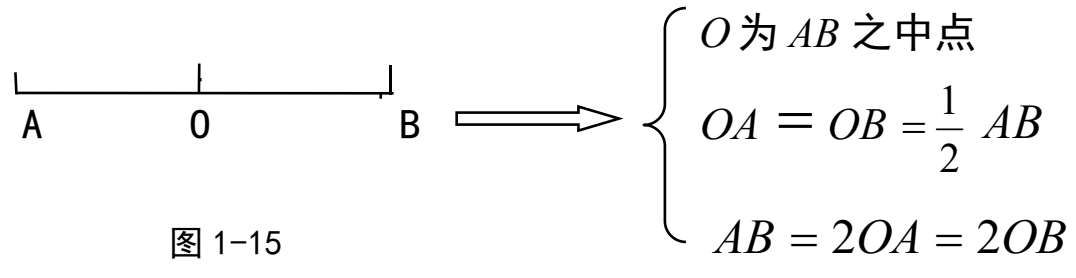
7.线段的中点
(1)线段的中点到两端点的距离相等。
(2)线段的中点可以用三种几何语言来表示(图1-15)。
(3)线段的中点(或“和差倍分”)都可以用 刻度尺或圆规 来完成。
8.角的平分线
(1)从一个角的顶点引出,把这个角分成两个相等角的一条射线,叫做这个

 。
。
(2)角平分线可以用三种几何语言来表示(图1-16)。
(3)角平分线(或N等分)都可以用 量角器或圆规 来完成。
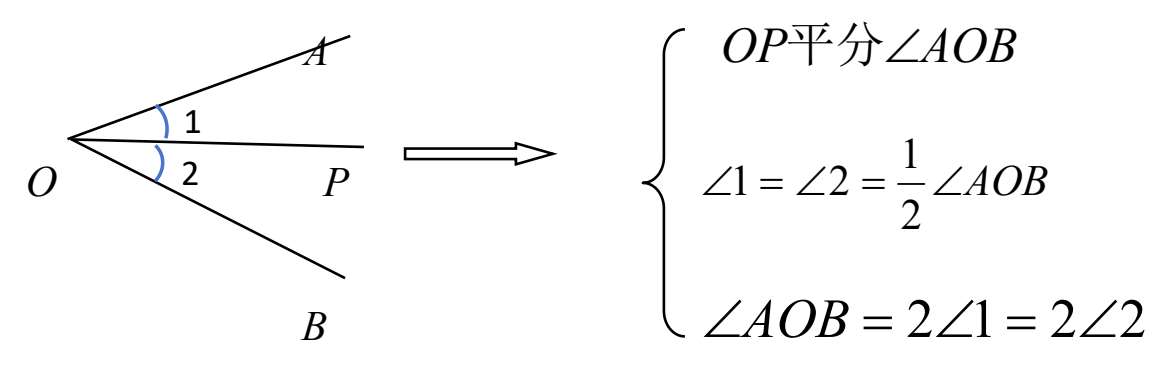
图 1-16
9.多边形和圆的初步认识
(1)多边形:由若干条不在同一直线上的线段首 尾顺次相连 组成的平面图形。
(三角形、四边形、五边形、六边形等都是多边形。)
三角形是最基本、最简单的多边形。任何一个多边形都可以通过适当的方法分解成若干个三角形。
正多边形:各边、各角都相等的多边形。
(2)多边形的对角线:连接多边形不相邻两个顶点的线段。
从n边形的一个顶点可以作(
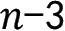 )条对角线,把这个n边形分成(
)条对角线,把这个n边形分成(
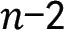 )个三角形。
)个三角形。
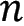 边形一共有
边形一共有
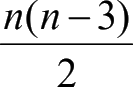 条对角线。
条对角线。
(3)圆的定义:
①一条线段绕其中的一个端点旋转一周,另一个端点所形成的封闭图形。
②平面内 到定点的距离等于定长的所有点的集合 。
(4)圆的有关概念:
弦、弧;圆心角、圆周角;扇形、弓形;圆的内接多边形和外切多边形。
1.线段、射线、直线的概念题;
2.线段中点或角平分线的有关计算;
3.线段或角的计算的分类讨论问题;
4.线段上的动点或角的旋转问题。
(此处如果有一线教师适当地加以演绎、指导,效果一定会更好!)