




1.理论基础
图像的旋转必须指明图像绕着什么旋转。一般图像的旋转是以图像的中心为原点,旋转一定的角度。旋转后,图像的大小一般会改变。图像旋转之后,会出现许多的空白点,对这些空白点必须进行填充处理,否则画面效果不好,称这种操作为插值处理。最简单的方法是行插值或是列插值。插值的方法是空点的像素值等于前一点的像素值,同样的操作重复到所有行。
和图像平移一样,既可以把转出显示区域的图像截去,也可以扩大图像范围以显示所有的图像。如图4-10所示,点( x 0 , y 0 ) 经过旋转 α 度后坐标变成( x 1 , y 1 )。
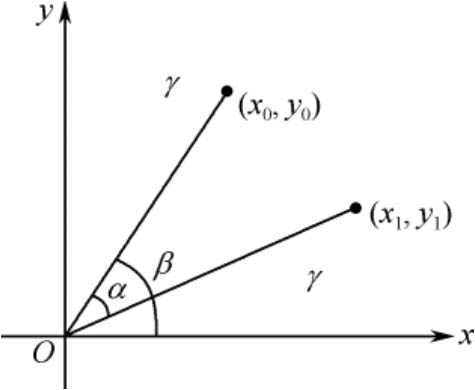
图4-10 图像旋转示意图
在旋转前
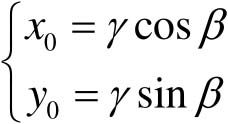
(4-19)
旋转后:
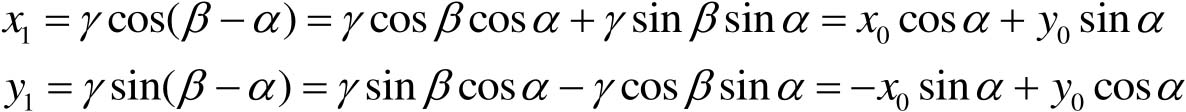
(4-20)
上述旋转是绕坐标轴原点(0,0)进行的,向右为 x 轴正方向,向上为 y 轴正方向,不妨设其为坐标系Ⅱ;而屏幕中的坐标一般以左上角为原点,向右为 x 轴正方向、向下为 y 轴正方向,设其为坐标系Ⅰ。如果是绕一个指定点( a , b )旋转,则先要将坐标系平移到该点,再进行旋转,然后平移回新的坐标原点。
下面首先推导坐标系平移的转换公式。如图4-11所示,将坐标系Ⅰ平移到坐标系Ⅱ处,其中坐标系Ⅱ的原点在坐标系Ⅰ中坐标为( a , b )。
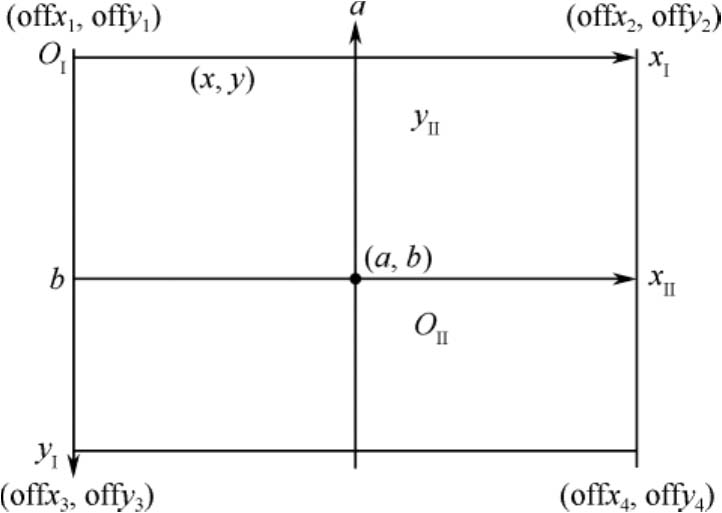
图4-11 旋转中心平移示意图
设图像的宽度为 w ,高度为 h ,得到
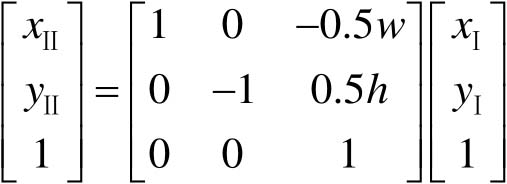
(4-21)
其逆变换矩阵表达式为:

(4-22)
按如下方法即可旋转图像:
①根据公式(4-21),将坐标系Ⅰ变成坐标系Ⅱ;
②根据公式(4-20),将该点顺时针旋转 α 角;
③根据公式(4-22),将坐标系Ⅱ变成坐标系Ⅰ。
假设图像在新的坐标系下,以旋转后新图像左上角为坐标原点,未旋转时中心坐标为( a , b ),旋转后中心坐标为( c , d ),则旋转变换矩阵表达式为:
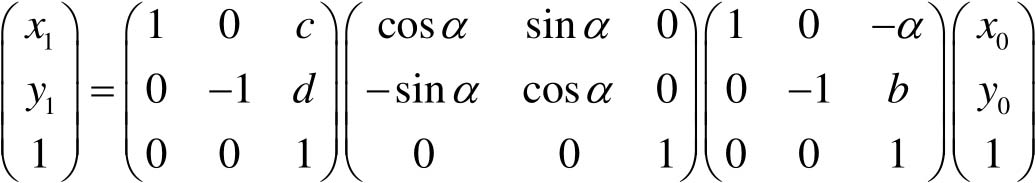
因此,
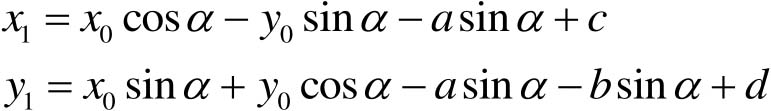
(4-23)
设未旋转时中心坐标为(0,0),则:
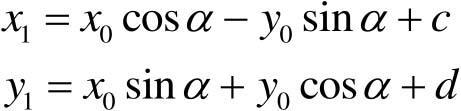
(4-24)
可以通过OpenCV模块中的函数cv2.getRotationMatrix2D()得到仿射变换函数cv2.warpAffine()的转换矩阵,这极大方便了对图像的操作。
2.函数说明
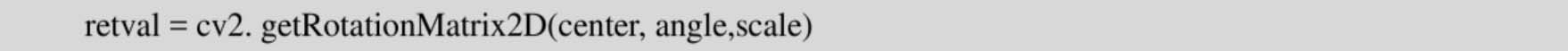
该函数用于得到仿射变换的转换矩阵。
center:旋转的中心点;
angle:旋转角度,正数为顺时针旋转,负数为逆时针旋转;
scale:变换尺度。
3.编程代码

4.效果展示
图像的旋转变换效果如图4-12所示。左侧为原始图像,右侧为处理后的图像。

图4-12 图像的旋转变换效果图