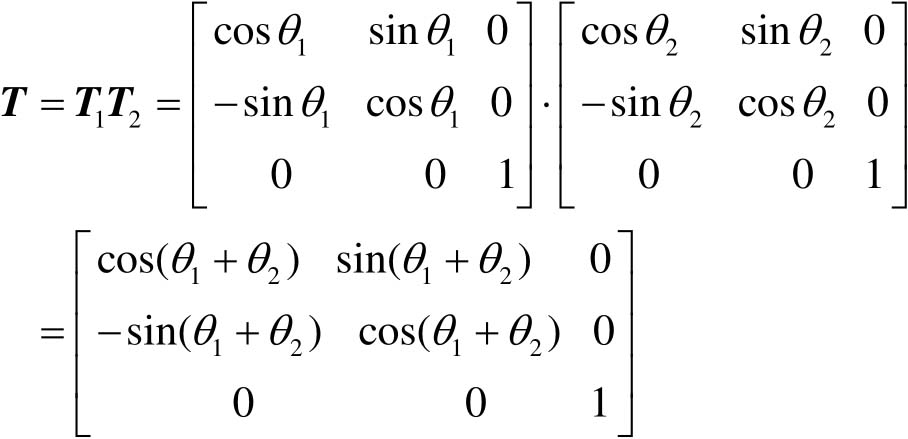4.1　概述

图像几何变换的实质就是改变像素的空间位置，并估算新空间位置上的像素灰度取值，使原始图像按照需要产生大小、形状和位置的变化，以改变图像中像素与像素之间的空间关系，从而重构图像的空间结构，达到处理图像的目的。从图像类型来分，有二维平面图像、三维立体图像的几何变换，由三维平面向二维平面投影变换等。从变换的性质分，有平移、镜像、缩放、转置、投影变换、旋转等基本变换及复合变换。

几何变换简单来说，就是建立变换前后像素之间的映射关系，通过这种映射关系能够知道原图像任意像素点在变换后的坐标位置，或者变换后的图像像素在原图像的坐标位置等。

数学公式如：

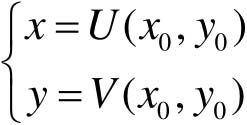
（4-1）

式中， x ， y 分别表示输出图像像素的横、纵坐标； x ₀ ， y ₀ 分别表示输入图像像素的横、纵坐标；而 U ， V 表示两种映射关系，通过输入的 x ₀ 和 y ₀ 来确定相应的 x 和 y 。

映射关系可能是线性关系，如：

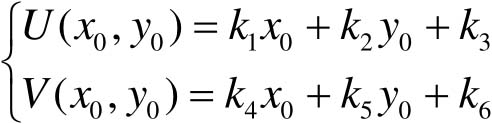
（4-2）

映射关系也可能是非线性关系，如：

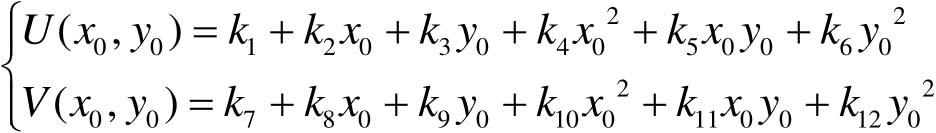
（4-3）

几何变换可以实现图像各像素点以坐标原点为中心的平移、缩放、镜像、旋转等各种变换。一般来说，变换后的点集矩阵=变换矩阵 T ×变换前的点集矩阵。

但是2×2变换矩阵 T 不能实现图像的平移以及绕任意点的缩放、镜像、旋转等变换。例如，令

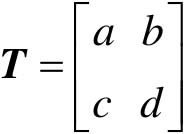
则几何变换为

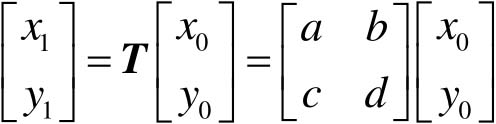
（4-4）

而平移公式为

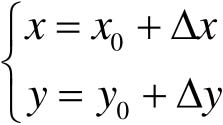
（4-5）

图像平移变换的矩阵形式：

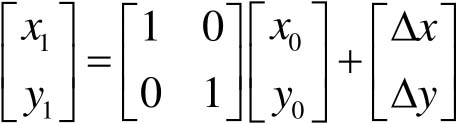
（4-6）

该变换不能表示为变换矩阵 T ×变换前的点集矩阵的形式，由于矩阵 T 中没有引入平移常量，故无论 a 、 b 、 c 、 d 取什么值，都不能实现平移功能。为了用统一的矩阵线性变换形式表示和实现几何变换，将 T 矩阵扩展为如下2×3的变换矩阵：

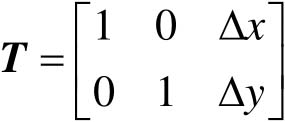
根据矩阵相乘的规律，在坐标列矩阵[ x y ]中引入第三个元素，扩展为3×1的列矩阵[ x y 1]，可实现平移。

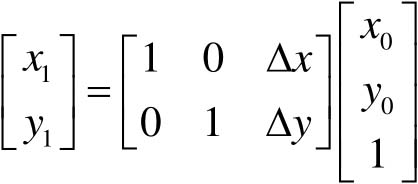
（4-7）

将2×3阶变换矩阵 T 进一步扩充为3×3方阵：

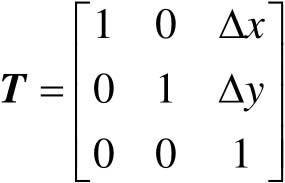
这样一来，以 n +1维向量表示 n 维向量的方法称为齐次坐标表示法。引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法，可以实现上述各种几何变换的统一表示。齐次坐标的几何意义相当于点( x ， y )投影在 xyz 三维立体空间的 z =1的平面上。

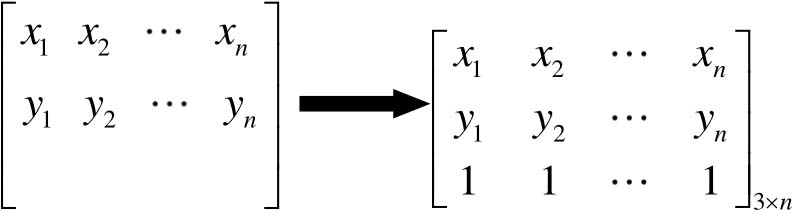
平移变换可以用如下形式表示：

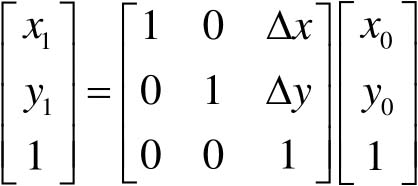
（4-8）

这里的几何变换全部采用统一的矩阵表示法，形式都如下：

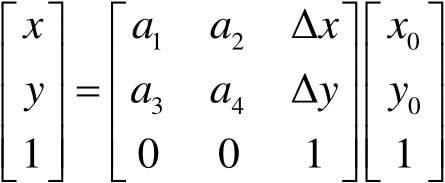
（4-9）

其中 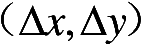表示平移量，而参数 a _i 则反映了图像的旋转、缩放等变化。将这些参数计算出，即可得到两幅图像的坐标变换关系。

对给定的图像连续施行若干次的平移、镜像、缩放、旋转等基本变换 F ₁ ， F ₂ ，…， F _N 后，所完成的变换称为复合变换。复合变换的矩阵等于基本变换的矩阵按顺序相乘得到的组合矩阵，又叫级联变换。若干次基本变换仍可用3×3阶方阵表示。

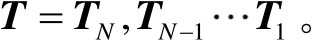
复合平移：

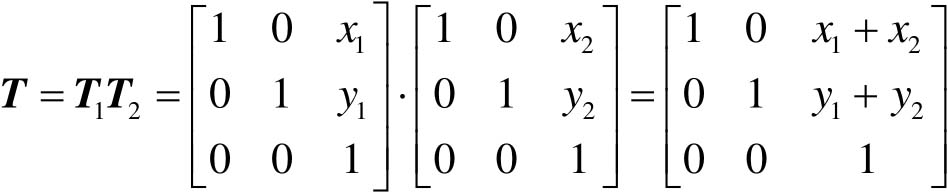
复合缩放：

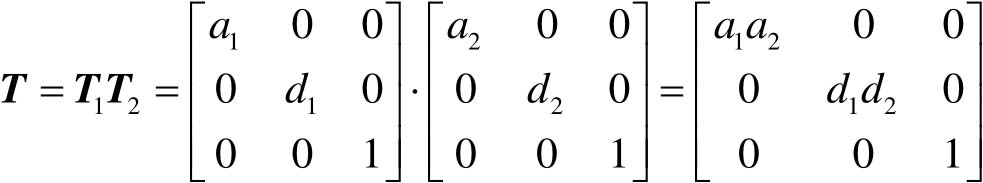
复合旋转： 7Z0XILvOF4dAUx4Szf/mG+F59Eojn+Q9HG8Y0YPiBGEGPny7UE9lddmUsubMM64e