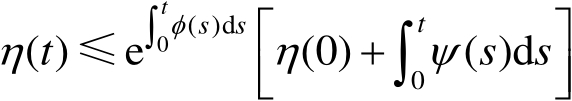Hölder
(霍德尔)
不等式:
设
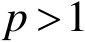 ,
,
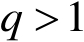 ,且
,且
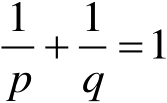 ,则对
,则对
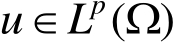 和
和
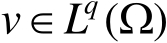 ,有
,有
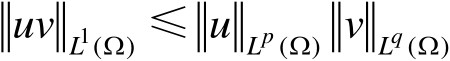
Bernoulli
(伯努利)不等式:
令
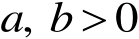 ,
,
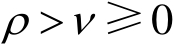 。设函数
。设函数
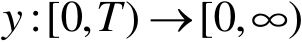 在
在
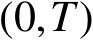 上可微,其中
上可微,其中
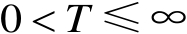 ,且对任意
,且对任意
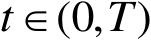 满足
满足
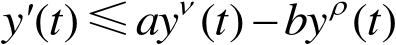
则
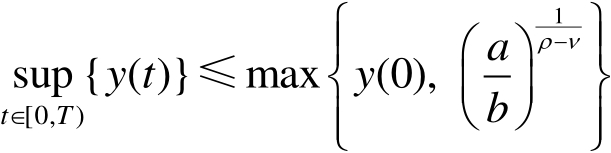
特别地,若
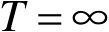 ,则
,则
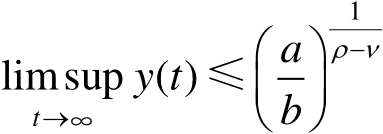
Young
(杨)
不等式:
设
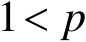 ,
,
 ,且
,且
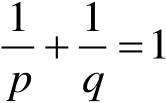 ,那么对任意的
,那么对任意的
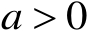 ,
,
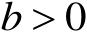 ,有
,有
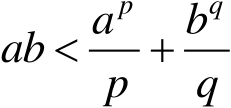
更一般地,设
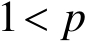 ,
,
 ,
,
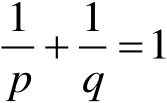 ,那么对任意的
,那么对任意的
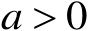 ,
,
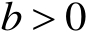 ,存在
,存在
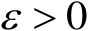 和
和
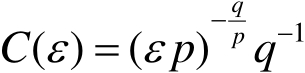 ,使得
,使得
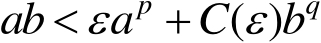
Gagliardo-Nirenberg
(加利亚尔多
−
尼伦伯格)
插值不等式:
设
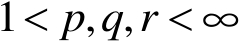 和
和
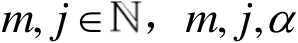 满足
满足
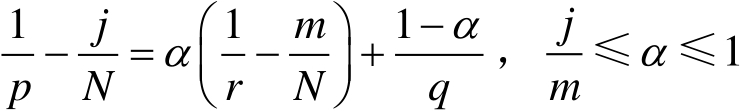
则存在常数
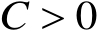 ,使得
,使得
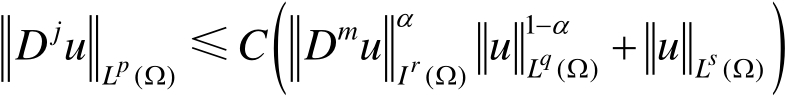
其中
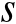 是任意非负常数。
是任意非负常数。
Poincaré
(庞加莱)
不等式:
设
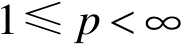 ,
,
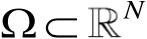 是有界区域,实值函数
是有界区域,实值函数
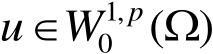 ,则存在常数
,则存在常数
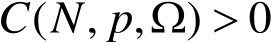 ,使得
,使得
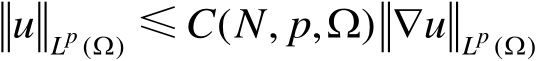
若
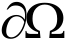 满足局部 Lipschitz(李普希兹)条件,
满足局部 Lipschitz(李普希兹)条件,
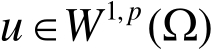 ,则存在常数
,则存在常数
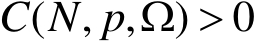 ,有
,有
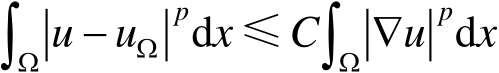
其中
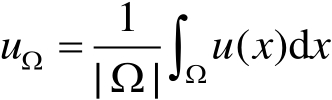 。
。
积分
Gronwall
(格朗瓦尔)
不等式:
设
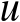 是
是
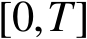 上的非负可积函数,且对几乎所有的
上的非负可积函数,且对几乎所有的
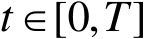 ,存在常数
,存在常数
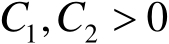 使得
使得
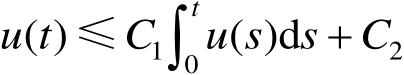 ,则对几乎所有的
,则对几乎所有的
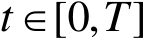 ,有
,有
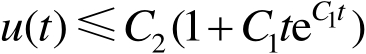
微分Gronwall
(格朗瓦尔)不等式:
假设
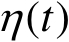 在
在
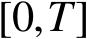 上是一个绝对连续的非负函数,且对几乎所有的
上是一个绝对连续的非负函数,且对几乎所有的
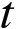 满足
满足
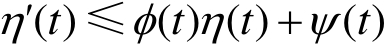
其中
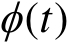 和
和
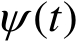 在
在
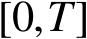 上都是非负可积函数,则对所有
上都是非负可积函数,则对所有
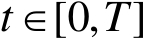 ,有
,有