




令
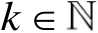 ,
,
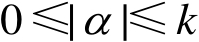 。记
。记
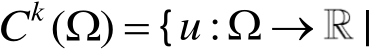 在
在
 上,
上,
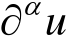 存在且连续},
存在且连续},
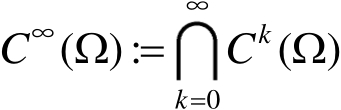 称为光滑函数空间。
称为光滑函数空间。
令
 ,记
,记
 ,显然
,显然
 表示在
表示在
 的某个紧子集外,
的某个紧子集外,
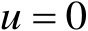 。
。
令
 ,记
,记
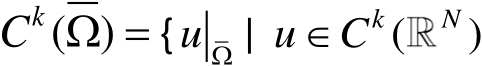 且
且
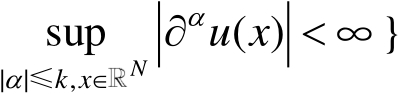 ,
,
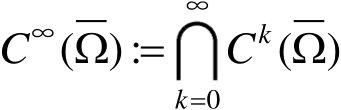 。
。
令
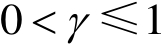 ,记
,记
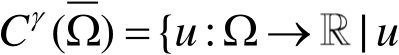 在
在
 上连续且有界,且
上连续且有界,且
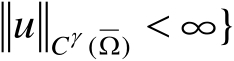 ,其中
,其中
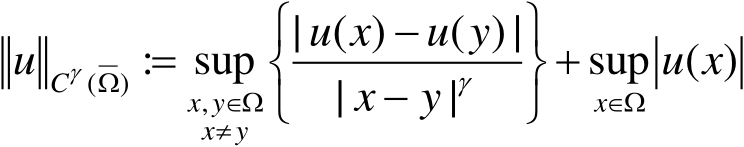 。
。
令
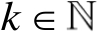 ,
,
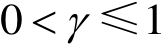 。记
。记
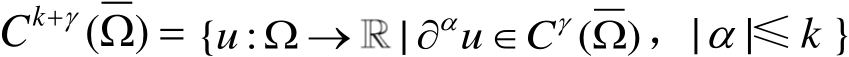 。若对任意的紧集
。若对任意的紧集
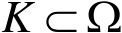 ,都有
,都有
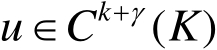 ,则
,则
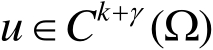 。
。
令
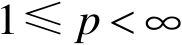 ,记
,记
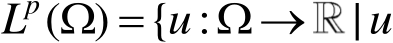 是勒贝格可测函数,且
是勒贝格可测函数,且
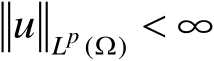 },其中
},其中
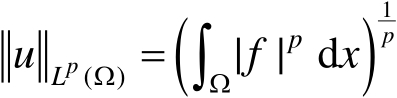 。
。
记
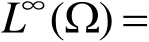 {
{
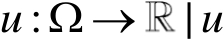 是勒贝格可测函数,且
是勒贝格可测函数,且
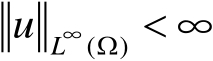 },其中
},其中
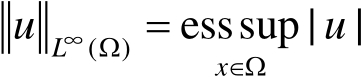 。
。
令
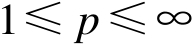 ,记
,记
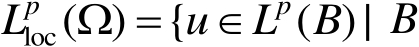 是
是
 中的任意开球,且
中的任意开球,且
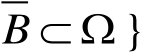 ,
,
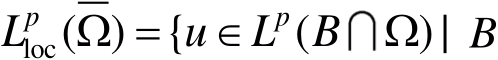 是
是
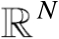 中的任意开球,且
中的任意开球,且
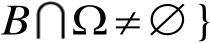 。
。
令
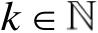 ,
,
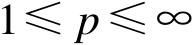 ,记
,记
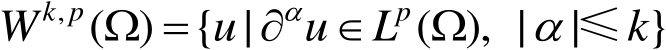 。在
。在
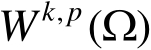 中,记
中,记
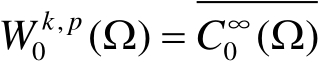 。
。
令
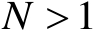 ,
,
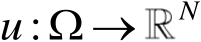 ,
,
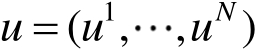 ,
,
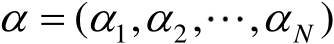 ,
,
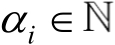 ,定义
,定义
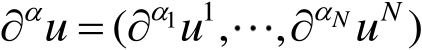 ,记
,记
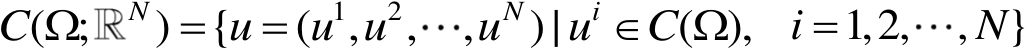 ,类似可以定义
,类似可以定义
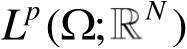 、
、
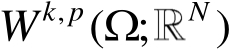 等。
等。
设
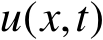 是定义在
是定义在
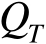 上的函数,
上的函数,
 ,记
,记
 ,其中
,其中
设
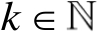 ,记
,记
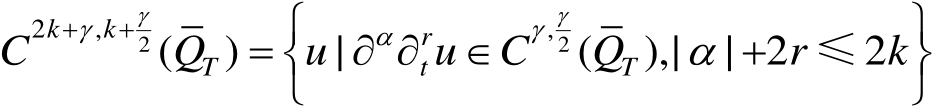 。
。
设
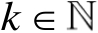 ,
,
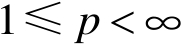 。记
。记
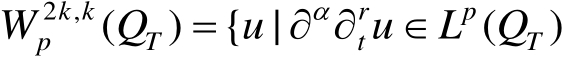 ,
,
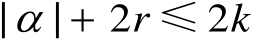 ,
,
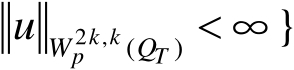 ,其中
,其中
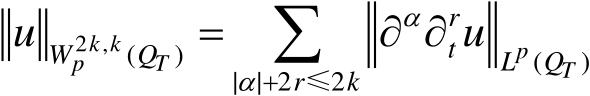
嵌入定理
设
 为一有界区域,
为一有界区域,
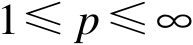 。
。
(1)若
 满足一致内锥条件,则当
满足一致内锥条件,则当
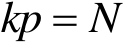 时,有
时,有
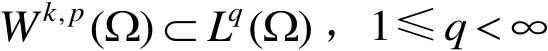
当
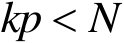 时,有
时,有
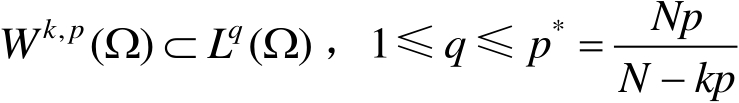
(2)若
 适当光滑,则当
适当光滑,则当
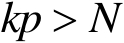 时,有
时,有

紧嵌入定理
设
 为一有界区域,
为一有界区域,
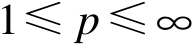 。
。
(1)若
 满足一致内锥条件,则当
满足一致内锥条件,则当
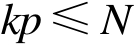 时,下列嵌入是紧的
时,下列嵌入是紧的
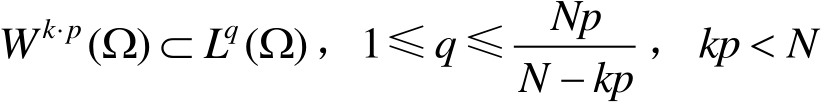
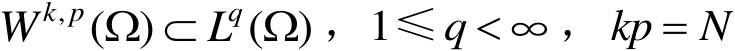
(2)若
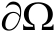 适当光滑,则当
适当光滑,则当
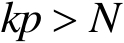 时,下列嵌入是紧的
时,下列嵌入是紧的
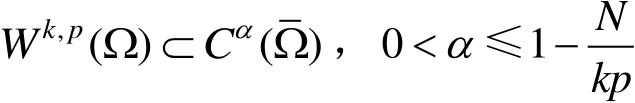
注:
以上紧嵌入定理对
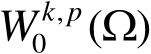 同样成立。
同样成立。
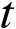 向异性嵌入定理
设
向异性嵌入定理
设
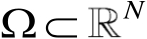 为一有界区域,
为一有界区域,
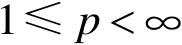 。
。
(1)若
 满足一致内锥条件,则当
满足一致内锥条件,则当
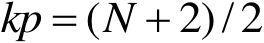 时,有
时,有
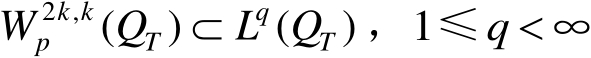
当
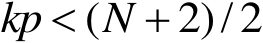 时,有
时,有
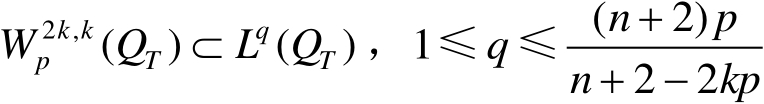
(2)若
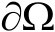 适当光滑,则当
适当光滑,则当
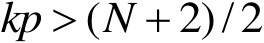 时,有
时,有
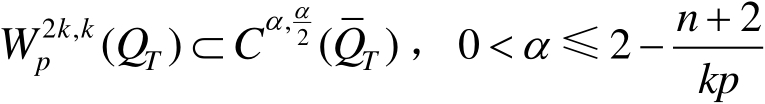
设
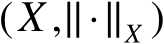 是赋范线性空间,
是赋范线性空间,
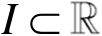 是开区间,
是开区间,
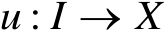 。令
。令
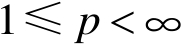 ,记
,记
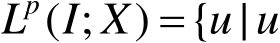 是可测函数,
是可测函数,
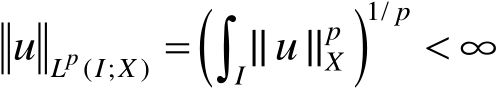 且
且
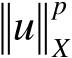 在
在
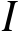 上可积};
上可积};
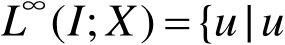 可测且几乎处处有界,
可测且几乎处处有界,
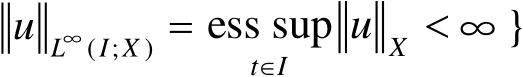 。
。
设
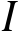 有界,
有界,
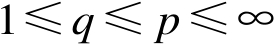 ,则
,则
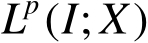 嵌入
嵌入
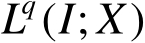 。
。
设
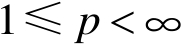 ,
,
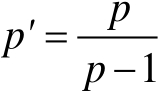 ,
,
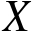 是自反的或
是自反的或
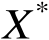 是可分的,则
是可分的,则
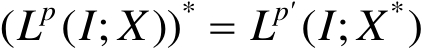 。
。
设
 ,记
,记
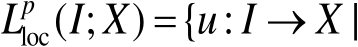 对任意紧集
对任意紧集
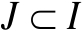 ,
,
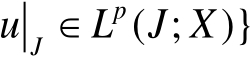 。
。
记
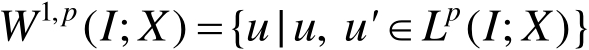 ,其中
,其中
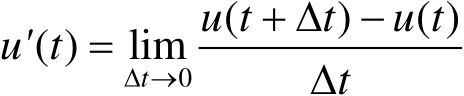 。
。