




 在数学中被认为错误的那个规律缘何能够在大自然中成立
在数学中被认为错误的那个规律缘何能够在大自然中成立
我们据此已经详细地说明,按照平方对力进行测算在数学中被认为是错误的,除了老的或者笛卡尔主义的力的尺度之外,数学不允许其他力的尺度。然而,在上一章的不同地方,我们已经使读者建立了尽管如此仍将平方测算引入大自然的希望,现在是兑现我们的承诺的时候了。这种冒昧将使我们的大部分读者感到诧异,因为从这里似乎可以得出,数学并不是不会骗人的,对它的陈述提出上诉也是可以的。然而,事情并非确实如此。如果数学陈述自己关于所有物体的规律,那么,大自然的规律也将包括在内;而且,希望有一种例外,那是徒劳的。然而,它却借助于各种公理确定了自己关于物体的概念;对于这些公理它要求,人们就它的物体而言必须以这些公理为前提条件,但这些公理却具有这样的性质,即它们就数学的物体而言并不允许并排除某些特性,但在大自然的物体那里却必然遇到这些特性;因此之故,数学的物体是与大自然的物体迥然不同的事物。所以,某种东西对前者来说可能是真的,但却不可转用到后者身上。
我们现在要看一看,在大自然的物体中所遇到、而数学就自己的物体而言不允许的特性,究竟是一种什么样的特性;此外究竟是什么原因使得前一种物体成为与后一种物体完全不同类的事物。数学不允许自己的物体拥有一种不是完全由作为它的运动的外部原因的东西产生的力。因此,它不允许物体中有别的力,除非这种力是从外部在物体里面造成的;就它的运动的原因而言,人们每一次都精确地、以同样的尺度再次遇到这种力。这是力学的一个基本规律,但其前提条件却也不允许除笛卡尔主义的测算之外的其他测算成立。不过,我们马上就会证明,大自然的物体完全是另一种情况。大自然的物体自身就有一种能力,自动地在自己里面增大由其运动的原因从外部在它里面唤起的力,以致在它的运动里面,就能够有并非从运动的外部原因产生的、甚至大于这种原因的单位的力;因此,这种单位的力不能用度量笛卡尔主义的力的同样尺度来度量,也可以有另一种测算。我们要以一件如此重要的事情所要求的那种极为精确缜密的态度来探讨大自然物体的这种特性。
一如我们在第3节已经看到的那样,速度自身并不包含一种力的概念。因为它是运动的一种规定性,也就是说,它是物体的这样一种状态的规定性,在这种状态中,物体并不运用自己拥有的力,而是拥有这种力却什么也不做。但它原本就是物体在静止时所拥有、即物体以无限小的速度所拥有的那种力的数目;也就是说,它是这样一个数目,其中物体在速度无限小的时候所拥有的力就是单位。这一点,根据尤林那个杰出事例(第110节)的提示,也就是说如果我们按照类似的方式,像他把速度看做是由两个相同的部分构成的那样,就其无限小的各部分来衡量它,就可以最清晰地由剖析的方式得到解释。
为了精确地知道究竟是什么规定了力的概念,我们必须以下面的方式进行。力被正确地凭借终止它并在物体中消解它的障碍来测算。由此得出,一个物体,如果在它里面没有一种在自身中保持障碍要消除的那种状态的努力,就会根本没有力。因为如果不是这样,那么,障碍要终止的那种东西就会像是一个零。
运动是力的外部现象,而保持这种运动的努力则是能动性的基础,而速度则表明,为了拥有全部力,就必须假设速度是多少倍。这里我们想把那种努力称为强度;因此,力等于速度与强度的乘积。
为了有一个能够更为清晰地说明这些概念的例子,且假设有一根4段的弹簧a、b、c、d。
 如果我们确定,这4段中的每一段单独开始伸展的速度是1,那么,由4段这样的弹簧组合而成的整根弹簧ad在自由伸展时的初始速度就是4;看起来好像可以由此得出,这根4段的弹簧施加给一个物体的初始速度比1段的弹簧造成的初始速度大4倍。然而,强度在4段的弹簧中是在1段的弹簧中的1/4;正是以某种尺度向一个不动的支点压迫这4段弹簧中的1段的力量,也成4倍多地压迫4段的弹簧,因为单个弹簧如果以这种方式与其他3段联在一起,它的支点就是可动的支点,从而4段的弹簧的坚硬度,或者换句话说也一样,4段的弹簧的强度,也就失去了传递它们速度的那种东西。因此就发生了这样的事情:4段的弹簧虽然在自由伸展时其初始速度要大于1段的弹簧4倍,但它给予一个物体的初始速度却并不大于该物体从1段的弹簧能够获得的初始速度。这一点可能有助于解释强度的概念,并说明,缘何在测算力的时候必须把强度考虑在内。
如果我们确定,这4段中的每一段单独开始伸展的速度是1,那么,由4段这样的弹簧组合而成的整根弹簧ad在自由伸展时的初始速度就是4;看起来好像可以由此得出,这根4段的弹簧施加给一个物体的初始速度比1段的弹簧造成的初始速度大4倍。然而,强度在4段的弹簧中是在1段的弹簧中的1/4;正是以某种尺度向一个不动的支点压迫这4段弹簧中的1段的力量,也成4倍多地压迫4段的弹簧,因为单个弹簧如果以这种方式与其他3段联在一起,它的支点就是可动的支点,从而4段的弹簧的坚硬度,或者换句话说也一样,4段的弹簧的强度,也就失去了传递它们速度的那种东西。因此就发生了这样的事情:4段的弹簧虽然在自由伸展时其初始速度要大于1段的弹簧4倍,但它给予一个物体的初始速度却并不大于该物体从1段的弹簧能够获得的初始速度。这一点可能有助于解释强度的概念,并说明,缘何在测算力的时候必须把强度考虑在内。
像是一条线,也就是说如同速度
如果一个物体的力是这样的,即它只是在一个时刻致力于保持运动的状态,至于速度则随它的便,那么,这种努力或者强度对所有的速度来说都是同样的;因此,这样一个物体的全部力都仅仅与它的速度成比例;因为因数中的一个始终是相同的,所以,显示力的量的乘积与第二个因数成比例。
对于这样一种运动来说,不断地从外部补偿在物体中每时每刻都在消失的力是必要的,而如果物体要以这种方式作出不断的运动的话,力就永远只是一个不断的外部推动的结果。不过由此也可以清楚地看出:如果与此相反,物体的力是这样的,即它在自身包含着足够的努力,以给定的速度始终如一地、不断地从自身出发不需要外部援力保持运动,那么,这种力就必然是迥然不同的,必然也极为完善得多。
这是因为:由于对前一种力来说,其强度对所有的速度都是相等的,即是无限小的,只是通过大量各种单位的速度才多样化的,所以,后一种力与此相反,在大量各种单位的速度中总是与速度成比例,并与之相乘,其乘积则是力的真正尺度。因为其强度无限小的有限速度提供了一种力,其中恰恰这种强度在速度无限小的情况下形成的力就是单位。因此,如果一个物体要在自身中充分地确立这种速度和力,以便拥有完整的努力持久地在自身中保持它们,那么,它的强度就必须与这种速度或者力成比例。在这种情况下,由此就产生出一种全新的力量,它是与速度成比例的力与相等于速度的强度的乘积;因此,这乘积也就等于速度的平方。也就是说很容易就可以理解,由于物体以无限小的强度在速度有限的情况下所拥有的力如同表现这种速度的一条线,而强度则如同一个点,所以如今强度同样如同一条线,而由此产生的力则如同一个从前一条线的运动产生的面,而且是如同平方,因为所说的这些线相互之间是成比例的。
人们可能会觉察到,我在这里完全没有考虑质量的差别,或者把质量设想为相等的;其次,就我所说的运动而言,我把空间看做是空荡荡的。
据此,一个物体,在自身中充分地确立自己的运动,以致从它的内在努力出发就可以充分地理解,它将自由地、持久地、不受阻碍地在自身中把这运动保持到无限,这样的物体就具有一种以其速度的平方为尺度的力,或者如我们想称谓的那样,具有一种活力。与此相反,如果它的力并不是在自身中拥有保持自己的根据,而是仅仅以外部原因的在场为基础,这种力就与单纯的速度成正比,也就是说,它是一种惰力。
但如今,我们要衡量一个物体的力,看它在通过一个外部原因的作用而在物体里面最先产生时是什么样子。在这种情况下,它肯定是以外部原因的在场为依据,并且在外部原因未唤起推动的那个时刻,它并不存在于物体里面。因此,在它依据外部原因的时刻,它具有这样的性质,即如果外部原因不在场,它就会马上消失。这是因为,物体是否能够在这个时刻之后在自身中确立在它里面唤起的这种力,以及在此之后从中产生出什么,我们现在不谈这个问题。所以在这个时刻,力的强度无限地小,因而仅仅以外部推动为依据的力自身和单纯的速度一样,也就是说是惰态的。但是,如果在此之后这个物体将赋予它的这种力确立在自己内部的力中,从它的努力中产生出对运动的一种持久自由的保持,那么,它在这种情况下就不再是一种惰力,而是一种以平方为尺度的活力,与惰力的关系就像一个面与一条线的关系。由此也就很清楚,一个物体以这种方式,当它自己自由地继续施加给它的速度时,就自动地在自身中无限地加大它从外部的机械原因获得的力,并把它提高为一个迥然不同的类别,因而我们在第115节所作的说明在此得到了证明,活力被完全排除在数学的审判权之外。
此外,人们由此看出,活力不能由一个外部的力——无论它多么地大——在一个物体中造成;因为只要一个力依赖外部的原因,那么它就总是像我们已经证明的那样,与自己的简单速度成正比;相反,它必须从物体自然力的内在源泉获得与平方尺度相应的规定性。
我们已经证明,如果一个物体在其自身中充分完备地说明自己运动的原因,以致从其力的性质出发就能够理解,这种力在物体中将不变地、自由地永远得到维持,那么它就具有一种活力;但如果它在自身中根本不能说明自己的力,而是由此而依赖于外部,那它就具有一种惰力;后者无限地小于前者。这马上就得出了结论:如果这个物体虽然有一些、但却不能完备地在自身中说明自己的力,那么它的力就有一些接近活力,并且与惰力有一些区别;在这两个终极的界限即完全的惰力和完全的活力之间,必然还存在着无限多从前者向后者过渡的中间单位。
此外,由此还可以借助连续律得出:一个物体,它在开始的瞬间拥有一种惰力,并且在此之后获得一种活力,后者与惰力的关系如同一个面与产生它的线的关系,则这个物体只是在一个有限的时间里获得这种活力的。因为如果要设定,它不是在开始瞬间的一个有限的时间里,而是直接在开始瞬间之后无限小的时间质点中获得后一种力的,那么这无非是说,它在开始瞬间自身中就已经拥有了活力。因为连续律、甚至数学都证明,无论我说物体处在其运动的开始瞬间还是说它处在开始瞬间之后无限小的时间质点上,这都是一回事。但是,力在运动开始的点上是惰态的。因此,人们不可能说在此之后它是活力,同时断定运动中的这种活力只是在外部原因起作用后经过一个有限的时间才能在运动中找到。
也就是说,物体的自然力在自身之中延续着从外部接受来的压力,并且由于它借助一种得到延续的努力而将事先像一个点的强度在自身中积累起来,直到它变得像一条线,这条线与从外部在它里面激发的与速度成正比的力也是成正比的,这样,它就由此而将从外部获得的、事先也仅仅像一条线的力自身积累起来,以致它如今像一个平面,在这个平面中,外部给予的速度和力表现为一条边,而从物体内部自己生成的强度构成另一条边,后者与前者成正比。
物体的力虽然还不是活力、但却在朝着这个目标前进的那种状态,我称之为力的变活或者活化。
因此,力上升为活力的那段时间位于两个端点之间,即始点与力完全成为活力的那个点之间;在这段时间里,物体在自身中还没有充分地确立自己的力。在此,也许我的读者会想到发问,物体在这段时间里究竟是怎样能够自由并且一致地维持和继续自己被给予的速度,因为在这种情况下它在自身中还没有充分地确立自己的力和运动,从而还不能自己来维持它。对此我的答复是:力在这段时间里虽然还不具备这样的性质,使得从它出发就可以理解一种永远自由且不减弱的运动,即使它不凭借内在的努力而继续得到提高。不过,力维持自己的努力在这种方式中是否不完备,在此暂不讨论。要问的只是:尚未如此增长、以致能够不减弱且不断地维持运动的力,其强度却至少能够经历直到完成活化所必需的这段时间而维持运动。至于这种情况不仅是可能的,而且事实上也是如此,这一点由此也得到了说明,因为在这整个时间段里,每一瞬间都有强度的新元素在物体中产生,这个新元素在一个无限小的时间质点里维持着既定的速度,从而这一强度经过整个时间段在物体中产生的所有元素就在这整个时间段的所有瞬间里维持着同一速度,从与第19节的对照中就可以清晰地说明这一点。
但是如果我们假定,在活化尚未完成的时间段里,物体突然停止进一步积累强度的元素,停止使力完全成为活的,在这种情况下,会发生什么事情呢?显而易见,在这种情况下,物体将仅仅在自身中确立并在自己的运动中继续不断地维持与它在活化的这段时间里已经获得的那种强度成正比的速度单位,而为了达到完全活化就要求比现实存在更大强度的其他单位的速度,就必然突然消失和中止。因为现存的强度在自身只能确立这种速度的一个部分,并且也不再在每一瞬间都产生强度的新元素来在所有的瞬间维持既定的速度,因此其余的部分必然自动地消失。
因此,如果一个自由运动的物体遇到一个阻力,它在以自己的全部速度达到完全活化之前运用自己的力量来克服这一阻力,那么,它所使用的这种力量就如同它所达到的强度与之成正比、并与之相适应的速度单位的平方,因而这种力量能够在给定的时间里成为活的,或者这种力量也如同它所达到的这种强度的平方;物体并不以其他的单位做什么事情,或者仅仅按照简单速度的尺度起作用,但相对于其他的力,这一点并不值得注意。
据此,一个在自由运动中将自己的速度毫不减弱地维持到无限的物体,就具有一种活力,即具有一种以速度的平方为尺度的力。
然而,这也是与这一规律相联系的条件。
1.物体自身必须包含着在一个畅通无阻的空间中不变地、自由地并且持久地维持其运动的根据。
2.从以上所证明的已经看出:物体并不是从将它置于运动之中的外部原因获得这种力的,相反,这种力是在外部刺激之后从物体自身内部的自然力产生的。
3.这种力在物体中是在一个有限的时间里产生的。
这一规律是力的新测算的主要根据;关于这种新测算我要说,如果我的判断与我所论及的如此伟大的人物相比的微不足道性允许我以这样的权威性说话,那么,我要用它来取代笛卡尔和莱布尼茨的测算。此时,我并非不乐意使自己相信:这一规律也许能够规定这样一个目标,而未切中这一目标在所有民族的哲学家中间造成了分裂和争论。活力在被从数学中放逐之后,被接纳入了自然界。人们将绝对不能责难两位伟大的世俗智者中的任何一个——无论是莱布尼茨还是笛卡尔——犯有错误。即便是在自然界中,莱布尼茨的规律也不会不同于经过笛卡尔的测算缓和之后的样子。如果人们在不同的机敏人物的人格中把人类理性与自身统一起来,并且即便在他们相互矛盾的情况下也找出这些人物的缜密决不会完全错过的真理,这在某种意义上叫做捍卫人类理性的荣誉。
问题的关键在于,世界上存在着自由运动,如果没有外部的阻力,这种自由运动将持久而且毫不减弱地维持自身。这样问题就清楚了,在自然界中肯定存在着活力。行星自由持久的运动,以及证明自由运动的物体仅仅按照阻力的规定而丧失自己的运动、没有这种规定就将永远维持这种运动的无数其他经验,都提供了这种保证,断定了自然界中活力的存在。
然而由此还可以清楚地看出:数学根据其判断的明晰性不容许其物体有自由运动。因为它不容许必然使运动自由和持久的东西,也就是说,不容许物体从其内部产生一种既不是从外部原因产生也不能来源于外部原因的努力和力。因为除了从是其运动原因的物体中产生的力之外,数学不承认一个物体中还有别的力。
尽管迄今的考察和证明具有这样的性质,即无非是仅仅就事情的本性所允许而比得上数学的概念及其明晰性,但我还是想满足那些认为凡是仅仅具有一种形而上学外表的东西都值得怀疑的人们;他们绝对要求一种经验,使经验成为推论的基础,显示出一种使他们能够更为满意地利用这些考察的方法。也就是说,我将在这一章的结尾从一个经验出发以数学的明晰性说明:在自然界中确实能够发现拥有速度之平方的力。
这些先生们可以从第二章所有证明的结果过渡到这一点:一个诸如此类的力不可能是外部机械原因的一个作用,因为如果允许力仅仅是造成运动的那个原因的作用,那么,除了按照单纯的速度进行的测算之外,就不可能进行任何别的测算。这将把测算引导到这种力何以能够从物体的内在自然力产生的方式,并逐渐地使它过渡为我关于活力的本质所进行的那些考察。
我曾经说过,力的自由的、从物体内部出发得到继续的持续期是真正的标志,人们只有从这标志出发才能得出力是活力并且以平方为尺度的结论。我非常高兴的是,在我上面
 援引的贝努利先生的文章中极为精确地发现了这一思想。作为一位单纯的几何学家,他虽然不是以地道的形而上学语言,但却完全清楚明白地表述了自己的见解。他说道:Vis viva est aliquid reale et substantiale,quod per se subsistit,et quantum in se est,non dependet ab alio; —Vis mortua non est aliquid absolutum et per se durans etc.etc.
援引的贝努利先生的文章中极为精确地发现了这一思想。作为一位单纯的几何学家,他虽然不是以地道的形而上学语言,但却完全清楚明白地表述了自己的见解。他说道:Vis viva est aliquid reale et substantiale,quod per se subsistit,et quantum in se est,non dependet ab alio; —Vis mortua non est aliquid absolutum et per se durans etc.etc.
 [活力是某种实在的、实体性的东西,它凭借自身存在,且它如何自己存在,并不依赖于他物。——惰力并不是某种独立的、凭借自身而持久的力……]
[活力是某种实在的、实体性的东西,它凭借自身存在,且它如何自己存在,并不依赖于他物。——惰力并不是某种独立的、凭借自身而持久的力……]
这一引述给我的考察带来不少好处。这位数学行家通常带着某种怀疑看待他相信是出自吹毛求疵的形而上学区分的推论,这种怀疑迫使他拒绝给予他的赞同;我不得不担心,他对我的推论也会这样做;但在这里,事情是如此显而易见,以至于它会自动地显现在最严厉的几何学家的数学思考中。
我惊讶的是,由于贝努利先生在活力的概念中有这种醒悟,他已经有可能在他要证明这种力的方式上如此误入歧途。他很容易就能够得出,在就这种realis et substantialis,quod per se subsistit et est absolutum aliquid[实在的、实体性的、凭借自身存在的、绝对的某物]而言不确定的事例中、在不能发现应当引导到此的那些规定性的事例中,他将发现不了这种力;因为如他自己所看到的那样,这样的东西是活力的类标志,而就这种特性而言不确定的东西,也不能把人引导到活力上去。不过,他指的是在两个不相等的物体之间伸展开的弹簧的事例中发现活力,在这一事例中,不仅发现不了与其说应当引向所谓的惰力、倒不如说引向由上述区分标志说明的活力的任何东西,而且甚至所有在他确立自己的证明时所出现的力,都是某种quod non est aliquid absolutum,sed dependet ab alio[并非绝对的,而是依赖于他物的东西]。
我们由此再次被引导到,在一个复合的、明显的证明中听凭于单纯喝彩声的结果,离开我们在第88、89、90节称颂并收益颇丰地利用的方法的导线,该是多么危险;也就是说,事先考虑必然地附属于作为证明主题的事物的概念,然后研究证明的条件是否也在自身中包含着以确立这些概念为目的的相关规定性,该是多么绝对地必要。
我们已经证明,活力在自然界中的存在仅仅建立在这样的前提条件之上,即自然界中存在着自由的运动。但现在,从一个物体根本的、几何学的属性出发,却难以找到应当使人根据我们在前文已经阐明的东西认识到像为了提供一种自由的、不变的运动而要求的这样一种能力的证据。
因此可以得出,活力并不是被认做一种必然的属性,而是某种有条件的、偶然的东西。如莱布尼茨先生特别地在《神正论》中所承认,他自己已经认识到了这一点;而丹尼尔·贝努利
 先生则通过据他认为人们证明活力所必须利用的方式证实了这一点。也就是说,人们必须预设一个基本的等式,即dv=pdt;在这个等式中,dv表示速度的元素,p表示造成速度的压力,dt则表示压力造成无限小的速度所用的时间的元素。他说,这是人们必须接受的某种有条件的东西。
先生则通过据他认为人们证明活力所必须利用的方式证实了这一点。也就是说,人们必须预设一个基本的等式,即dv=pdt;在这个等式中,dv表示速度的元素,p表示造成速度的压力,dt则表示压力造成无限小的速度所用的时间的元素。他说,这是人们必须接受的某种有条件的东西。
活力的其他辩护者们对作出不同于莱布尼茨先生的判断感到不安,于是就众口一词。尽管如此,他们还是在绝对是几何学上必然的事例中寻找活力,并且自认为可以在其中找到;这毫无疑问是极为令人惊异的。
赫尔曼先生以同样的方式尝试这样做,但却没有因活力的偶然性而把自己搞糊涂。不过,作为前提条件的关于莱布尼茨思想的良好评价以及绝对作为目的的意图使他陷入了一种无疑值得注意的错误结论。我觉得,并不能轻而易举地找到某个人物,让他想到作出这样的推论:人们必须把a和b两个量合并起来,在其结合中予以考察,因此人们必须把它们一起相乘;但尽管如此,这却是完全按照赫尔曼先生这样一位如此伟大的推理大师发生的。他说,“在下落时获得力的一个新元素的物体,却已经有了一个速度,于是必须把这个速度一起予以考察。因此,人们必须把它已经拥有的速度u、它的质量M和速度的元素或者——这是一回事——重力g和时间的乘积——即gdt——合在一起。因此,dV或者活力的元素等于gMudt,也就是说,等于这里标出的量的乘积”
 。
。
我们的学说体系自己就包含着,一个自由地、不变地运动的物体在其运动的开始并不拥有其最大的力,相反,如果它已经运动了一段时间,它的力就会更大。我觉得,每一个人都有某些能够证实这一点的经验。我自己就发现,在一杆火枪装得完全同样满的情况下,在其他条件都完全相同的情况下,如果我在离目标几步远的地方点燃火枪,则其枪弹就比我在离目标仅仅几寸远的地方向一块木头射击时射入木头更深得多。那些比我有更好的机会做试验的人们,有可能对此作出更为精确的、得到更好测定的检验。不过,经验教导我们,一个不变地、自由地运动的物体,其强度是按照我们在这里证明的定理在物体中产生,并且只有在一段确定的时间之后才获得其充足的量的。
如今,在我们奠定了力的一种新测算的基础之后,我们应当致力于指明那些与这种新测算特别关系密切的规律,它们似乎是构成了一门新动力学的脚手架。
我有能力阐述力的活化或者变活所遵循的一些规律,不过,由于本文致力于勾勒出力的这些如此新颖、如此出乎意料的属性的第一套方案,我不得不理所当然地担忧,我的那些特别渴望了解主要本质的读者们,会发现自己心烦意乱地卷入了对一件次要事情的深入研究,尤其是因为如果主要的东西首先得到保证并通过经验得到证实,是有足够的时间研究次要的事情的。
根据这一点,我将致力于仅仅尽可能清晰地揭示最普遍的、最值得考察的规律,它们与我们对力的测算密切相关,离开了它们就不能很好地理解这种测算的本性。
以下的说明阐述了一个完全未知的动力学规律,在力的测算中具有不凡的意义。
我们学到过:一个在静止中起作用的物体,只施加了一种惰态的压力,它与活力的种类截然不同,仅仅以一种简单的速度为尺度;在这一点上,无论是笛卡尔的所有追随者,还是莱布尼茨的学生们,都是意见一致的。但是,一个速度无限小的物体,本来就根本不运动,从而具有一种处于静止状态的力;因此,它具有单纯速度的尺度。
因此,如果我们要规定属于活力类别的运动,那么,我们就必须不把它们延伸到所有其速度可以任意大或者小的运动,也就是说,其速度在此不确定的运动。因为在这种情况下,对所有无限更小的速度单位来说,同一规律都将是真的,而物体也将能够在速度无限小的情况下拥有一种活力,这在前文不远处已被认定是错误的。
据此,按平方测算的规律不能不考虑其速度而对所有的运动有效,相反,速度在此是被一并考虑的。因此,就一些单位的速度而言,与它们相关的力并不能成为活的,只有速度达到一定的大小,力才能获得活化。在这个大小之下,就所有更小的单位而言,直到无限小的单位,这种情况都不会发生。
此外,由于力的完全变活是自由地、持久地维持运动的原因,因此可以得出,这种运动也不是对所有的速度来说都毫无限制地可能的,相反,它在这里同样必须是确定的,也就是说,如果物体要以某种速度提供一种持久的、不变的、自由的运动,则该速度必须具有某种确定的大小;在这个确定的单位之下,对所有更小的单位来说,这都是不可能的,直到对无限小的速度单位来说这种属性完全消失,运动的持续只是某种暂时的东西。
因此,运动自由的、不减弱的延续的规则并不是绝对地、而是仅仅从某个单位的速度开始有效,在这个单位之下,所有更小的单位都自动地消耗殆尽而消失,直到对无限小的单位来说运动仅仅持续一个瞬间,需要外部不断的补偿。所以,牛顿的规则在其不确定的意义上并不适用于自然界的物体:Corpus quodvis pergit in statu suo,vel quiescendi,vel movendi,uniformiter,in directum,nisi a causa externa statum mutare cogatur
 [任何物体,除非被外部原因迫使改变其状态,都将保持其状态,或者是静止,或者是不变的、直线的运动]。
[任何物体,除非被外部原因迫使改变其状态,都将保持其状态,或者是静止,或者是不变的、直线的运动]。
经验证实了这一说明;因为如果无限小的速度能够变活,那么它由于同有限力的变活成正比,就必须在无限小的时间里变活(第122节),因此,两个物体在仅仅施加重力的压力时,虽然仅仅拥有与其速度成正比的力,但一旦它们从哪怕是完全不可觉察的微小高度下落,它们的力就必然立即如同速度的平方;这是违背连续律和经验的。因为如同我们已经提到的那样,一个凭自己的重量没有压碎一块玻璃的物体,即便让它从一段极小的距离落到玻璃上,它也不具有击碎玻璃的力量;两个重量彼此相等的物体,如果有人让它们两个同样地向天平秤盘稍稍下落,它们也仍然保持着平衡,因为如果发生上述那种情况,这里就必然要产生严重的偏重现象。
因此,在规定关于物体在其中自由运动的中间空间的阻力的规则方面,这一规则必须被一并考虑在内。因为如果速度已经开始变得很小,中间空间就不再像以前那样多地促使运动的减弱,相反,运动将部分地自动消失。
我们正处在最典型的任务的中心,抽象的力学以前从来不可能完成这一任务。
我们提出一个这样的问题:物体是否就所有任意小的速度而言都能够达到力的完全变活,并且不变地自由地继续其运动。如今我们要研究一番,物体是否就所有较高的速度单位而言都能够提供同样的运动,也就是说,物体是否无论其被赋予的速度任意地大,都能够自由地继续并毫不减弱地维持其被赋予的运动,从而达到力的完全变活。
由于变活和以此为基础的运动毫不减弱的自由继续是物体内在自然力的一个结果,从而始终以后者能够在自身内产生前者并且自动地达到所要求的强度单位为前提条件,因而就提供所有更高乃至无限的活力单位而言,仅仅取决于这种自然力的大小和能力。但是,自然界没有任何大小确实是无限的,形而上学以一种清晰无误的方式阐明了这一点;因而每一个物体的所谓自然力都必然具有一个确定的有限的量。所以,它的作用能力也局限于一个有限的尺度。由此得出,它将自己在速度单位越来越大的情况下从自身产生活力的能力仅仅延伸到某个有限的目标,也就是说,物体不能直至无限地就所有的速度单位而言都以这种能力在自身中使力变活,从而使它在自由运动中无限地、毫不减弱地延续下去,相反,物体的这种能力在任何时候都仅仅有效到速度的某个大小,以致在高于这个大小的所有单位上,物体的能力都不再足以完成与该单位相符合的活化,并从自身中产生如此大的力。
由此得出,如果这个单位是确定的,那么,物体在一个外部的原因以更大的速度推动它时虽然顺从这一原因,并且只要外部的推动还在持续就接受这一运动速度,但一旦那个外部原因停止作用,就必然也立刻自动失去那个超过确定尺度的单位,而只保留下并自由地、毫不减弱地继续物体按照其自然力的尺度在自身中能够使其变活的那个单位。
此外由此得出,在自然界形形色色的物体中,这一些物体的自然力在不同的物体中将具有不同的大小,因而其中一个物体有能力自由地继续某种速度,而另一个物体却不足以达到这一点。
因此,这就是使某一个物体的力的活化能够进行的那种速度被包含在内的两个界限,在一个之下,在另一个之上,变活和自由运动不再能得到维持。
我们在第121节就已经知道,一个物体的力如果变活,就会比赋予它全部运动的那个力学原因大得多;因此,尽管一个物体运动的外部原因按照尤林方法的规定(第110节)仅仅以2个单位的力在它里面起作用,但该物体却以2个单位的速度拥有4个单位的力。现在我们想说明,一个障碍的力量比物体所拥有的力小得多,但尽管如此却能够夺走该物体的全部运动,因此,如同活力在前一种场合部分地由自己产生一样,在第二种场合在克服一个比它小得多的障碍时也会由自己消耗殆尽。
要证明这一点,我们只需要回到尤林的例子(第110节)。也就是说,驳船AB以等于1的速度自C向B运动。此外我们要设定,球体E沿着同样的方向,即沿着方向CB运动,但这是一种自由运动,利用的是活力,其速度等于2,因而这个球体仅仅以1个单位的速度与此处一根弹簧表现出来的、其力等于1的障碍R相遇;原因在于,就另一个单位的速度而言,它对于这个障碍来说并不以该单位运动,因为这一障碍同样有沿着同一方向的这种运动,从而物体在与这一障碍的关系中仅仅剩下1个单位的运动。但就1个单位的运动而言,力也仅仅等于1,所以球体是以等于1的力与同样只有1个单位的力的障碍相撞的,从而由于这个障碍而失去了它的这个单位的速度和力。在这种情况下,它仅仅剩下了1个单位的绝对运动,从而也只剩下了1个单位的力,可以再让另一个等于1的障碍来消除;因此,我们设定有一种活力、从而以2个单位的速度拥有4个单位的力的物体,将被两个障碍归于静止;这两个障碍中的每一个都只有1个单位的力,因而按照这种方式必须有2个单位在这个物体中自己消失,不需要被外部原因抵消或者克服。
因此,一个物体浪费自己的一部分活力不起作用的情况如下:两个或者多个障碍相继以这样一种方式阻挡它,这些障碍中的每一个都不是对抗运动物体的全部速度,而是像上一节的分析所说明的那样,仅仅对抗它的一个部分。
这一点如何与我们关于活力的概念相一致,可以按照以下的方式毫不困难地得到理解。如果一个物体的速度被分解为它的各个单位,那么,在这些单位中的一个单位上与其他单位相分离所发现、因而物体在不用其他单位而单独利用这个单位起作用时也使用的活力,就与这个单位的平方成正比;但如果物体以其全部速度不分解地同时起作用,那么,全部的整体力就与这速度的平方成正比,从而力的属于上述速度单位的那个部分就与该单位同整个速度的Rectangulum[乘积]成正比,它形成了一个比在前一种场合更大得多的量。因为例如,如果我们假定整个速度由2个单位构成,这2个单位相继被赋予物体,那么,在速度依然是1的时候,活力只能提高到一个等于1的大小;但在加上第二个单位之后,在物体中就不是仅仅又产生出只与第二个速度单位成正比的1个单位的力,而是自然力还以速度产生的那个比例将强度提高,使活力就整个速度而言达到4倍,因为力在所有分离开的单位上的总量只是2倍,这样,每一个单位在相关的作用中都能够与其他单位一起实施2个单位的力,因为每一个单位自身在单独的作用中只有1个单位的力。所以,如果一个具有活力、从而以2倍的速度具有4个单位的力的物体不是同时地、而是一个单位接一个单位地运用它的全部速度,那么,它就仅仅实施了2倍的力,物体就全部速度而言所拥有的其余2个单位的力则在自然力停止维持它之后,就像它在产生时自动地从自然力中产生出来一样,也自动地消失了。
这一说明以重要的结论来酬劳我们的努力。
1.除了障碍同时阻挡以活力侵犯的物体的全部速度并一起承受这缩短的所有单位之外,我们在任何地方都无法发现活力的全部作用。
2.与此相反,在障碍仅仅对抗速度的一个单位、从而无非是在分解开的各单位中逐次承受全部速度的地方,一大部分活力将自动丧失,而不是被障碍消除。如果有人相信障碍以这种方式消耗掉全部运动,也抵消了全部的力,那就大错特错了。在任何时候,障碍所承受的速度单位相对于运动物体的全部速度越小,这种损失就越可观。举例来说,物体拥有其活力所在的速度被分解为3个同等的单位,障碍每次都只能单独地对抗它们中的某一个,这样,虽然物体在这些单位的每一个上面都拥有活力,每一个单位的力却都等于1,因而相继克服这3个单位的障碍的力量也就等于3;但这个物体的全部活力却等于3的平方,即等于9。因此,这种方式,就有6个单位的力,即整体的2/3,没有外部的阻力而自己丧失了。与此相反,如果我们假定另一个障碍,它一次承受的不是上述全部速度的三分之一,而是其一半,因而不是把全部运动分解为3个,而是分解为2个单独的单位,那么,活力除了这一障碍消耗的东西之外,所承受的损失就仅仅等于2,即整体的1/2,因而就比前一种场合更小。以同样的方式,如果障碍一次对抗的单位是全部速度的1/8,那么,物体所浪费的就是全部力的7/8,其原因是不能在障碍中寻找的;依此类推,乃至无限。
3.如果障碍在每一瞬间所对抗的速度单位都无限小,那么在这种情况下,在被克服的障碍中就再也找不到活力的任何痕迹;相反,由于在这种情况下,每个个别的单位都仅仅与其直接假定的速度成正比地起作用,而全部速度的所有单位的总和又是相等的,所以物体的力无论是不是活的,其全部作用都仅仅与其简单速度成正比,而活力的全部大小都将自己消失殆尽,不会造成一种与它相符合的作用。也就是说,由于它本来等于一个由表示速度的直线的运动产生的平面,因此这第二个向度的所有元素都逐渐地自己消失,除了仅仅与产生者直线即速度自身成正比的之外,在作用中没有表现出一种力的任何其他痕迹。
4.因此,即使物体确实具有一种活力,也在任何地方都不能在所施加的作用中或者在被克服的障碍中发现一种活力的痕迹,除非障碍用来进行对抗的速度元素大小是有限的;但即使在这种情况下,也不能没有这一重要的条件,即速度的大小也不是可以任意小的,因为我们从第132节得知,速度要有一定的量,才能使以该速度运动的物体具有一种活力,而如果障碍阻挡的元素按照上述的量过于小,那么在它里面也不能感受到活力的任何作用。
我们将特别在本章结尾处看到这一说明极为显著的益处,在那里,它将有助于正确地说明和证实证明活力的重要经验。
由于重压的元素仅仅以无限小的速度发生,所以借助上一节第3条就可以非常清楚地知道,一个利用自己的运动克服重力障碍的物体,虽然力自身与速度的平方成正比,对障碍却只能施加与其速度自身成正比的作用,这完全是依照即便是这方面的经验也使人认识到的东西,我们在上一章已经详细地并且不仅仅按照一种方式看到了这一点。
因此,这里甚至表现出一种经验,它似乎仅仅认可笛卡尔的规律,而这事实上本来也除了这种测算之外,自身并没有显示出其他任何一种测算的征兆,但尽管如此,仔细想来却并不与按照平方进行测算——如果在其正确的意义上接受它的话——相抵触,反倒是给它留下了地盘。
所以,垂直升高的物体在克服重力的障碍时所产生的作用虽然无可争议地驳倒了莱布尼茨的测算,然而,它虽然没有真正地证明我们的活力,但尽管如此也没有取消它们。不过,如果我们把自己的注意力完全集中在这方面,那么,我们甚至还会在这里发现我们的测算的一些闪光。因为物体在它不能从自身中产生出同时作为其自由运动乃至活力的基础的内在努力或者强度的地方,它也不能自由地继续其固有的运动,并把该运动一直维持到外部的对抗逐渐地从它那里夺走为止。
从迄今所证明的东西,我们同时看到了那个极为著名的特技的原因,有人借助极小的障碍就能够抵消几乎无法制服的力量。也就是说,当要制服的力量建立在活力的基础之上时,人们并不是以一个一次性地作出对抗并且突然被制服的障碍来与它相对立的,因为这个障碍通常必须极为巨大,相反,毋宁说是以一个在其无限小的速度单位中逐渐地承受并消耗力的障碍与它相对立的;因为以这种方式,人们是凭借微不足道的对抗来挫败大得惊人的力量的,这就好像例如人们用羊毛袋来抵消攻城槌的撞击,如果攻城槌直接撞击到城墙上,就会把城墙撞毁。
此外可以得知,柔软的、在撞击时很容易压缩的物体,长时间并不通过撞击运用自己的全部力,毋宁说,它们仅仅施加很小的作用,而如果力和质量相同,但硬度却更大,这些作用就会大得多。我清楚地知道,这方面还有其他一些原因,除了我们谈到的那些原因之外,它们也为上述损失起到了自己的作用,或者毋宁说使得它显得是一种损失,但我们所列举的原因无可争议地是最重要的原因,而且是一种真正的损失的原因。
如今我们想研究一番,一个拥有活力、其质量被设想为无限小的物体,其作用究竟会是什么样的,因为这将使人认识到:在同样的条件下,如果两个物体的力都是活的,那么,假如人们把它们置于同样的条件下,一个物体的质量也任意地小,它们是否都能够施加与这些活力成正比的作用;或者毋宁说,每一个物体的质量都必须具有一定的大小,以致如果人们使它的质量更小,它所施加的作用就不能与它的活力成正比。
这是确定无疑的:如果一个质量有限的物体具有一种活力,那么,它的每一个部分无论多么小,也都必然具有一种活力,而且即便是它与其他部分分离开来运动,也都会具有一种活力;但这里的问题是,这样一种微小的、或者如我们在这里要假定的那样无限微小的粒子,如果把它置于一个更大的粒子与其活力成正比地起作用的同样条件下,它是否也能够独自在自然界造成一种与其活力成正比的作用。我们将发现,这是不可能发生的,一个具有活力的物体,如果它的质量小于按照我们要证明的规则必须具备的质量,在自然界中是不能起到与它的这种活力成正比的作用的,相反,质量越小,物体也就越不接近这一比例,直到当质量无限小时,物体虽然具有活力,但却以这种质量也只能与其简单速度成正比地起作用,而另一个具有同样的速度和活力、但却具有适当大的质量的物体,在同样的条件下将起到随其质量增长符合其速度的平方的作用。
事情仅仅取决于,自然界中所有应当被某种力制服的障碍,都不是立即就在接触点上以一种有限单位的对抗,而是先以一种无限小的单位来阻挡这种力,然后,在经过推动力所穿过的无限小的空间之后,推动力所遇到的阻力才变成有限的。凭借与真正的自然学说的一致,我把这一点作为前提条件,不打算在此列举证实它的一些根据。因此,牛顿的学生们抓住机会说,物体即便尚未相互接触,也对其他物体起作用。据此,即便我们不重视本来任何时候都存在于两个质量不同的物体的力之间的差异,而是仅仅考虑从我们的活力概念产生的差异,我们在一个质量无限小的物体向自然界的这样一些障碍施加的作用和它的质量达到某种有限的大小时所起的作用之间也发现了一种特别的差异。
也就是说,我们已经知道,即便物体具有一种活力,但这种活力被用来克服重压的障碍,物体的作用也仅仅与其简单速度成正比,作为活力标志的所有强度都不起作用地消失掉。但如今,重力的反压以无限小的外力一直作用到其质量的内部,即直接作用于推动物体的无限小的部分,因此,它的这种状态与虽然有活力、但质量无限小而向着自然界的某个障碍运动的物体相同,因为后者如我们已经说明的那样,也在这里总是承受着一种恰如就具有无限小外力的重力而言直接地对抗它的阻力;因此,这样一种无限小的质量也以同样的方式在自身消耗着自己的活力,并且对自然界的任何障碍都仅仅按照其速度的比例起作用。
由此可以清晰地得出,只有无限小的物体会遇到这种情况,相反,一个质量有限且确定的物体能够对同样的障碍施加一种符合其活力的作用,因为如我们所假定的那样,障碍只能从外部施加其阻力,不像重力作用到内部;因此,有限的物体在无限小的质量由于障碍继续不断的无限小的对抗而失去了自己全部速度的地方,只失去了无限小的东西,即什么也没有失去,相反,它的力仅仅用来克服无限小的质量不能达到的有限单位的对抗;所以就达到了如我们在第138节第4条所看到的那样,应当运用自己的活力来实现一种与自己成正比的作用的物体必然身处其中的条件。
如今,由于以有限的力、但却无限小的质量运动的物体在自然界的任何地方都不是与速度的平方、而是仅仅与速度自身成正比,所以,依据我们已经通过经常的运作必然已经熟知的那种推理方式可以得出,这个物体具有一种活力,因而在适宜的条件下
 ,哪怕质量是任意地小,它的速度也将与其活力成正比;相反,要使人们能够这样说,就要求质量达到某个量,而在这个尺度之下,这样一个物体对自然界的障碍的任何作用都不能与其活力成正比,无论这些障碍是什么样的;但是,质量的量越是低于这个确定的尺度,作用就越是偏离活力的比例,而就它之上的所有大小而言,关于它们都已经不言而喻,根本不会发现这种偏离。
,哪怕质量是任意地小,它的速度也将与其活力成正比;相反,要使人们能够这样说,就要求质量达到某个量,而在这个尺度之下,这样一个物体对自然界的障碍的任何作用都不能与其活力成正比,无论这些障碍是什么样的;但是,质量的量越是低于这个确定的尺度,作用就越是偏离活力的比例,而就它之上的所有大小而言,关于它们都已经不言而喻,根本不会发现这种偏离。
由此可以得出以下的说明:
1.一小块物质在与一个具有活力的大质量的牢固结合中,能够施加一种完全不同的、比它独自地与该质量分离时能够作出的大得出奇的作用。
2.尽管如此,这一区别却不是必然的,而是建立在自然界偶然的属性之上的;按照连续性规则,自然界的所有障碍早在以其有限的对抗与运动过来的物体对立之前,就远远地以无限小的单位开始了,或者说,尽管如此,自然界已经不允许有别的作用。
3.这并非毫无区别地都是真的:两个物体的力都是活的,它们的速度相等,它们的作用在同样的条件下与它们的质量成正比;因为如果它们的质量中的一个小于按照上述的规则应当具有的质量,那么,它的作用就会偏离速度的平方,从而比它仅仅按照质量的比例所应有的小得多。
4.甚至物体形状的改变也能够在没有质量变化的情况下就导致,尽管力与速度的平方成正比,但它们的作用在所引起的条件下却与其速度成正比;因此,一个具有活力的物体,之所以能够造成一种小得多的作用,乃是因为它的形状变化了,而无论是它的质量还是速度、活力或者障碍的性状都没有发生一点变化。举例来说,一个具有活力的金球要比同样的含金质量以同样的速度和力撞上同样的障碍产生的作用大得多,但问题是后者事先已被锻造成一张又薄又宽的金箔。因为尽管在这里就力而言没有发生任何变化,但形状的改变已经使它的极小的微粒在这里遇上障碍,与它们彼此孤立地撞上障碍完全一样,因此根据刚刚证明的东西,它们早已不能以其活力并与活力成正比地起作用了,相反,它们所起的是一种或者接近简单速度之尺度的作用,或者是一种与简单速度一致的作用。在此恰恰相反,如果质量以一个坚硬的球的形状撞上障碍,在该球如此之小的面积上与它接触,以致该球在如此之小的空间里遇到的抵抗的无限小的元素,不能消耗掉质量的运动,从而活力就完好地保存下来,仅仅被用来克服这一障碍有限单位的对抗;同样,显而易见的是,它以前一种形状覆盖了障碍绝对大的面积,从而虽然质量相同,却蒙受到在障碍每一个点上遇到的无限小的外力的更大得难以置信的阻挡,所以必然更容易能够被该障碍消耗殆尽,活力或者完全丧失,或者丧失大部,而这在前一种情况是不会发生的。
然而,我从现在证明的规律得出的最重要的结论是完全以自然的方式从中产生的结论,即液态物体通过撞击与其速度的平方成正比地起作用,尽管它们即使作用在此应当与其活力成正比,也依然不一定按照其速度的平方
 、而是按照其速度的立方的尺度来起这种作用;虽然这一点像尤林先生已经清楚地说明了的那样
、而是按照其速度的立方的尺度来起这种作用;虽然这一点像尤林先生已经清楚地说明了的那样
 ,否定了莱布尼茨先生的活力,但它与我们的活力力量却并不抵触。
,否定了莱布尼茨先生的活力,但它与我们的活力力量却并不抵触。
因为液体分散为可以视为无限小的极精细部分,并不结合成为连在一起的固态物体,而是所有的部分前后相继地、都独立地、与其他部分分离地起作用的;因此,当它们撞上自然界的任意一个障碍时,它们承受着无限小的物体如我们已经说明的那样总是承受的那种活力的损失,因而尽管它们的力与其速度的平方成正比,但却仅仅与其速度成正比地起作用。
李希特
 先生白白地耗费大量精力来避开尤林的这一打击。他的事情一筹莫展,因为它是与以下规则相结合的:力所处的比例,无异于作用所处的比例。
先生白白地耗费大量精力来避开尤林的这一打击。他的事情一筹莫展,因为它是与以下规则相结合的:力所处的比例,无异于作用所处的比例。
最后,每一个人也都能够轻而易举地理解,具有自由运动和活力的物体在一个液态的中间空间中为何仅仅与其速度的平方成正比地承受阻力,而不由此损害我们的活力;尽管这与莱布尼茨的测算相抵触,按照他的测算,这一阻力必然与速度的立方成正比。
有无数的经验来证实我们迄今所谈论的这一规则。尽管这些经验并没有得到精确的测定,但它们依然是真实无误的,拥有普遍一致的赞同。
因为如果我们不给自己的规则留下地盘,我们就必须设定:一个物体,即便它是那么微小,在同样的条件下也能通过碰撞产生出与一个大的质量在人们使它们的速度与其质量的平方根成反比、或者按照笛卡尔的规则在它们的速度与这些质量成反比的时候同样大的作用。然而,经验与此相抵触。因为每个人都一致认为,即便人们给予一根羽毛或者阳光下的一粒浮尘如同人们自己所要求的那种单位的速度,它们也不能通过一种自由运动来产生一颗炮弹的作用;我相信,也没有人会猜测如果它们以如此大的速度在自由运动中遇上一团固态的物质或者墙壁,它们中的某一个能够击碎这团物质或者穿透墙壁。这一切虽然不能通过任何安排妥当的试验予以检验和证实,但无数这方面在类似的场合——尽管不是以如此之大的程度——出现的经验,导致没有人怀疑所引起的结果。
但如今却不能否认,所说的小物体在上述对其速度的规定中必然与大物体具有同样的力,无论是按照笛卡尔的、或者莱布尼茨的、还是按照我们的力的尺度都是如此:所以,除了小物体必定施加一种比按照它的力所应当发生的那样更小的作用之外,没剩下别的方法来解释这一点;小物体的活力绝大多数都没起作用就被抵消了,这恰恰就像我们在第143、144、145节关于小物体所证明的那样。
属于那些除了笛卡尔主义的测算之外不给其他测算留下踪迹、从而显得与我们力的尺度相抵触的经验的,最终还有弹性物体通过碰撞产生的运动;我们在上一章已经详细地讨论过这些运动,它们都在完全真实无误的试验中被认定为真的。它们也在事实上凭借与此不可分割地结合在一起的前提条件否定了莱布尼茨先生的平方测算:也就是说,在其产生中力消耗殆尽的那些作用,总是与力相等。我们的测算拥有理由充足的优越性,不服从这一规律,因而避开了这一打击。
我们从以上所说已经知道:活力并不是某种从外部借助一个外在的原因、例如借助一次撞击能够在一个物体中产生的东西;这已经能够向我们说明:我们将不把被撞击物体的活力视为撞击物体的作用,并力图用前者来测量后者。但是,全部困难的现实解决,如果人们确实认为能够在这里找到一种现实解决的话,就存在于下文之中。
所有力学专家都必定知道:一个弹性物体以其全部速度并不是一下子就作用于另一个物体,而是通过它在该物体中相继产生的诸多无限小单位的连续积累。我没有必要讨论这方面的特殊原因;对我来说,获得我这方面的一致赞同就够了;而且每一个人都认识到,没有这一前提条件,就不能解释任何运动规律。这方面的真正原因也许是:因为按照一根弹簧的本性,弹性仅仅与足以绷紧它的那个单位的速度相对抗;因此,就它所承受的任何无限小单位的压力而言,都总是只承受撞击物体的一个无限小单位的速度,从而在任何时刻都不是对抗全部速度,而是仅仅对抗无限小单位的速度,并把它接纳入自身,直到逐渐的积累将全部速度都以这种方式过渡到承受物体之中。
根据上文由此可以得出,由于撞击物体在此只是相继地以其速度的逐个无限小的单位起作用,它也仅仅简单地与其速度成正比地起作用,对它尽管如此却能够拥有的活力没有损害。
莱布尼茨先生关于一成不变地维持世界上力的某个大小的常用规律,还是一个显得在此需要仔细检验的题目。因此显而易见的是:即便在迄今的考察中有某种得到论证的东西,它在通常被接纳的意义上也无法成立。但是,我们的测算在这一章中究竟将引入什么,它怎样才能满足使得上述莱布尼茨规律如此值得赞扬的普遍和谐与秩序的规则,尽管我有能力就此提出一些纲要,但我们的计划的性质和我在一个如此生硬未经处理的题材上理所应当担心我的博学读者的注意力出现的疲倦,却不允许我作出相应的勾画;我不得不担心,也许已经过于伤害这种注意力了。

我们如今处在经验的国土上;但在我们能够于此有所收获之前,我们必须确定借口对此拥有理由充分的权力并想把我们排挤出去的那些要求已经被根除了。如果我们忽视以著名的穆森布罗克先生为创始人、因而富有说服力和洞察力的那个试验以及力学证明,不对此维护我们采纳的力的学说的话,我们迄今为止所作的努力就会是不完备的。穆森布罗克先生想借助这一试验在莱布尼茨的意义上捍卫活力,因而我们就有义务检验这一试验。
通过仔细地衡量这一试验我们得知:它并没有产生预期的结果,毋宁说是证实了笛卡尔的力的尺度。而这一点也重新证实了我们经常提到的那个说明:只要人们认为只能在外部原因中找到一种按照平方测算的力的起源,那就发现不了它的任何痕迹,真正的活力不是由外部在物体中产生的,而是在有外部力量的情况下在物体中从内部的自然力产生的努力的结果;因此,所有仅仅承认外部起作用的原因、以便由此出发规定承受物体中力的尺度的人们,即便他们正确地作出判断,也永远不会发现不同于笛卡尔的测算的东西。
穆森布罗克先生的证明
 如下:
如下:
假定有一个中空的圆柱,上面固定一根弹簧。从圆柱中必须伸出一根布满洞孔的棍子,它通过一块硬铁皮的开口插在上面。如果用力将钢制的弹簧压向这块铁皮并且压紧,以致棍子进一步从铁皮的开口伸出,那么,通过在铁皮突出的一面将一根钉子插入棍子的某个洞孔里,就可以将弹簧固定在这种张力中。最后,如果将圆柱当做一个钟摆悬挂在某一个机器的两根绳子上,在此之后抽出钉子,那么,弹簧就将迅速弹开,并给予圆柱某个速度,通过达到的高度就可以认识这个速度。且称这个速度为10。然后通过在圆柱中装入所需要的重量,使它比事先重两倍,并和之前一样压紧弹簧。如果在这种情况下再使它弹开,则借助它所达到的高度可以发现,速度有7.07个单位。由此穆森布罗克作出了如前的论证。
弹簧两次都同样地被压紧,因而在两个场合拥有同样的力,由于它每一次都运用自己全部的力,所以它两次带给圆柱的力是相等的;因此,一个物体以1倍的质量和10个单位的速度所拥有的力必然等于在另一个拥有2倍的质量和7.07个单位的速度的物体中所发现的力。但是,这无论如何都是不可能的,除非按照质量与速度平方的乘积来测算力;因为速度所有其他可能的函数都不允许这一等式,但惟独按照平方的测算数字10和7.07的平方quam proxime[极为接近地]与质量1和2成反比,因此,它们与对方质量的乘积相等。
因此他得出结论,应当不是按照速度的尺度,而是按照速度的平方来测算力。
我有义务将我针对这一论据所要阐述的提醒不致弄得过于庞杂;因此,我就不再提及我在这里还能够提出的理由充分的质疑,即伸展开的弹簧压力的元素即便是按照莱布尼茨学派所承认也仅仅是惰力,因而无论是这种力还是由此赋予物体的力的元素,都必须仅仅按照速度来测算,从而作为这些元素之总和的全部力也是如此;相反,我想按照一种每个人都熟悉的、自身具有几何学的清晰性的力学方式行事,但同时也详细地阐释某种东西,不是像在事情不足够容易,只能更简略地把握它的时候那样,而是为了一劳永逸地完全根除就弹簧的作用而言迄今为止在力的测算的争论中流行的一切混乱。
穆森布罗克先生说道:弹簧在两种场合都同样地被压紧,因而它在两种场合里具有同样的力,但它每次都把自己全部的力传递给圆柱,因而它也在两次伸展时都给予其圆柱同样的力。这既是证明的基础,但也是失误的基础,尽管这种失误不仅是穆森布罗克先生个人的,而且宁可说是莱布尼茨力的测算的所有捍卫者共有的。
如果谈到一个弹簧全部的力,那么,这无非是指它的张力的强度,它等于自己所作用的物体在一瞬间从弹簧的压力所获得的力。就这种力而言,人们当然可以说,无论弹簧所作用的物体是大还是小,这种力都是同样的。然而,如果人们留意弹簧在某段时间里通过连续的施压带给一个物体的力,则显而易见:以这种方式带给物体的力的大小取决于同样的压力在物体中积累所用的时间的长短;时间越长,同样被压紧的弹簧在这段时间里赋予物体的力也就越大。但如今,人们可以把弹簧在推动一个物体、直到它完全伸展开来时所用的时间任意地延长,也就是说,如果人们把这里应当被推动的质量像无人不知的那样增多的话;因此,人们还可以根据被同一根弹簧推动的质量被增多还是被减少,任意地使弹簧在张力相同的情况下通过其伸展时而给予更多的、时而给予更少的力。由此可以看出,说弹簧通过其伸展将它全部的力都给予它所推动的物体,这种表述是多么违背自然。因为它给予物体的力不仅是一个取决于弹簧的力的结果,而且根据被撞击的物体处在这根弹簧的压力下的时间是长还是短,也就是说,根据这个物体的质量是大还是小,它还是一个取决于被撞击物体的性状的结果;弹簧的力就其自身来看,无非就是其伸展的元素。
从现在起,很容易就可以防止穆森布罗克证明中的混乱。
2倍重的圆柱在弹簧伸展时比另一个具有1倍质量的圆柱更长时间地蒙受弹簧的压力。与前者相比,弹簧以同样的张力更快地推动后者,并与后者一起以更短的时间通过其伸展的空间。但由于弹簧在每一瞬间压迫圆柱的力的元素是相等的(因为其速度的元素与其质量成反比),所以,较重的圆柱通过弹簧的推动比较轻的圆柱获得了更多的力。因此,认为力在两种场合相等的那种测算是错误的,也就是说,力不能按照速度的平方来测算。
如果人们还想知道圆柱从同一根弹簧所获得的速度究竟为什么恰恰如此成比例,以致速度的平方与质量成反比(这一比例本来就是诱引莱布尼茨先生的辩护者们的那个比例)的原因,我们也可以毫无困难地澄清这一点,用不着因此就求助于不同于笛卡尔尺度的另一种原因。
因为从力学的首要根据出发就可以得知:在均匀加速度运动(motu uniformiter accelerato)中,所达到的速度的平方与所通过的空间成正比;因此,如果两个都处在motu uniformiter accelerato[均匀加速度运动]中的物体速度的元素不相等,那么,它们在这样的运动中所达到的速度的平方就处在由空间和这些元素构成的复合关系之中。但现在,在穆森布罗克的试验中,同样被压紧的弹簧传递给每一个圆柱的运动是motu uniformiter accelerato[均匀加速度运动],而它们以这样的加速度运动在弹簧伸展到其最大扩张的点期间所通过的空间是相等的,因此,在此获得的速度的平方与弹簧的压力赋予每一个圆柱的速度的元素成正比,也就是说,与圆柱的质量成反比。
从现在开始,我着手阐述无可争议地证明了自然界中按照速度的平方测算的力的现实性和存在的那些试验和经验,它们将以一种成功的说服来酬报我的亲爱的读者,感谢他们如今让蹩脚的文章引起了所有煞费心机的注意。
我只同足够熟悉关于活力的争论性质的那些人们打交道。因此,我预先假定,我的读者们对里乔卢斯
 、格拉维桑德
、格拉维桑德
 、波莱尼
、波莱尼
 和穆森布罗克先生的声名狼藉的试验有足够的认识,这些人通过测量物体借助碰撞在柔软物质中造成的压力来研究物体的力。我只是想略微提及:大小与质量相等的球体从不同的高度自由地下落到柔软的物质中,例如下落到动物油脂中,在动物油脂中砸出坑洞,坑洞与球体下落出发的高度成正比,也就是说,与其速度的平方成正比;而如果他们的大小相等,但质量却不同,他们下落出发的高度则与质量成反比,在这种情况下在柔软物质中砸出的坑洞被发现是相等的。对于这些试验的正确性,笛卡尔学派不会提出任何异议,有争议的仅仅是由此得出的结论。
和穆森布罗克先生的声名狼藉的试验有足够的认识,这些人通过测量物体借助碰撞在柔软物质中造成的压力来研究物体的力。我只是想略微提及:大小与质量相等的球体从不同的高度自由地下落到柔软的物质中,例如下落到动物油脂中,在动物油脂中砸出坑洞,坑洞与球体下落出发的高度成正比,也就是说,与其速度的平方成正比;而如果他们的大小相等,但质量却不同,他们下落出发的高度则与质量成反比,在这种情况下在柔软物质中砸出的坑洞被发现是相等的。对于这些试验的正确性,笛卡尔学派不会提出任何异议,有争议的仅仅是由此得出的结论。
莱布尼茨学派由此出发以如下方式作出了完全正确的论证。柔软物质对抗侵入物体的力的障碍,无非就是其各个部分的联系,因此,物体在侵入柔软物质的时候所要作的惟一事情就是分开它的各个部分。但是,这一贯穿全部柔软质量的联系是到处相同的,因此,阻力以及物体为征服柔软物质所必须使用的力的量与被分开的各个部分的总和成正比,也就是说,与砸出的坑洞的大小成正比。但根据以上引证的试验,坑洞的大小与侵入物体速度的平方成正比,因此,这些物体的力与其速度的平方成正比。
笛卡尔的辩护者们不能对此提出任何有力的质疑。然而,由于他们之前曾以无可置疑的确定性发现,活力已受到莱布尼茨学派同样援引的数学的谴责,因此他们打算尽自己所能摆脱困难,因为他们毫不怀疑,那个看起来确认了几何学所不允许的某种东西的试验必定是骗人的。对此,我们在上文已经作了必要的提醒,现在我们只是想看一看,笛卡尔学派用来使上述试验无效的,究竟是一种什么样的托词。
他们指责说,莱布尼茨学派在这里又一次没有注意造成这些坑洞所用的时间。就克服这种柔软物质的障碍而言,与克服重力一样,时间同样是一个症结。被压出的坑洞并不是在同样的时间里造成的。简而言之,他们相信,就克服重力障碍而言根据时间提出的质疑是有效的(事实上它也确实有效),而现在,他们想,人们在这里可以再次将它引入轨道,同样成功地用来反对活力。
我清楚地知道,莱布尼茨学派简单地打发了这一控诉,他们除了别的东西之外,还让两个底面积不同的圆锥下落到柔软物质中去,此际造成坑洞的时间必须是相等的,尽管如此结果却同前面的一样;然而,我还是想抛弃这种好处,从根本上清除笛卡尔学派造成的困难。
除了考虑一个物体应当克服的重压的阻力为什么不与空间、而是与时间成比例的原因之外,人们下一步也就没有该做之事了。但是,根据也就在于此。当物体克服一根重力弹簧时,它并不是由此清除了它的效用,而是仅仅给它提供了一个平衡力量,但它尽管如此却仍毫不减弱地继续保持其对抗,以便在物体承受其对抗的期间一直以同样的单位作用于物体。如果物体要通过制服来同时可以说是击溃每一根重力弹簧并消除它的力,那么毫无疑问,由于每一根弹簧都具有同样的力,所以物体所承受的阻力就等于所有被击溃的弹簧的总和而时间则可以是任意的。但是,每一根弹簧即使被物体所克服,也都保持着自己的压力,并且在物体仍处于这种压力之下期间继续向物体施压,从而就单独一根弹簧所起的作用来说不能被视为一个个别的、不可分的压力,相反,它施加的是一系列相互依赖的压力,物体处在这些压力之下的时间越长,这些压力就越大;举例来说,在空间的各部分中,当物体的运动比较慢时,在每一个点上停留的时间就比在运动比较快时更长,因此,物体在前一种场合要比在后一种场合承受一个更长系列的相同压力。
然而,就柔软物质的分离而言,这完全是另一种情况。柔软物质的每一个元素都有一种相同的相互联系的力,由此它也从分离它们的物体夺走了一个相等单位的力,但也正是由此,它也同时被分离开,从而不再继续作任何抵抗,物体在柔软物质处逗留的时间在此之后却可以是任意长的。因为在这里,弹簧同时被与其阻力相等的作用所粉碎,因而不能继续起作用,就像自身不可毁坏的重力弹簧一样。所以,柔软物质对侵入物体的阻力与它所击溃的弹簧的总和成正比,也就是说,与该物体砸出的坑洞成正比,在这里与时间没有一点相干。
莱布尼茨学派有理由庆祝相当令人满意地战胜了笛卡尔学派重要的失误。这一巧合通过其敌手们遇到的同样命运报复了指出如此众多的失误所带给他们的辱骂。莱布尼茨学派自认为在这样一些没有活力的场合里能够发现活力,但究竟是什么妨碍了这种发现?笛卡尔学派却在确实有活力的场合里不能看到活力,而在这些场合里,没有任何人能够大受蒙蔽却无视活力。
因此,上述试验证明了自然界中这样一些以速度的平方为尺度的力的存在;然而,我们先行的考察说明了在什么样的条件下这样的力不能成立,以及什么样的条件是这样的力能够获得地盘的惟一条件。如果按照我们的说明来利用这一切,人们就不仅会对活力获得一种足够的确定性,而且还会对活力的本性获得一个比以往所有或者所能有的概念不仅更正确、而且也更完备的概念。这一有计划的试验的特殊性质还提供了一些能够引起特别注意的非同寻常的特征;然而,在有兴致的读者的注意力被如此众多复杂的研究搞得疲劳不堪,也许除了结束这些考察之外再也没有别的愿望之后,我绝对不能再探讨这些特征了。
不过,还有惟一一点我不能不提及,因为它印证并清晰地说明了先行的规律。我们所计划的试验证明了按照速度自身的平方测算的力,因此,按照第138节第4点,本试验中障碍的任何元素对抗的速度都必须以有限的单位产生;因为如果它们像重力的压迫那样以无限小的单位产生,那么,对重力的克服就和在重力那里一样很少能使人看到一种按平方测算的力(第139节)。因此我们想证明,柔软质量的每一个元素的对抗都不是像重力那样以无限小的速度,而是以一个有限的单位产生的。
如果把球状物体在柔软物质中砸出的圆柱形坑洞分成诸多重叠的圆盘,它们的厚度无限小,那么,这些圆盘中的每一个都表现出被移动质量的元素。因此,这些圆盘中的每一个都从侵入物体夺走了其速度的一个无限小的部分,因为它们加起来夺走了该物体的全部速度。但由于每一个圆盘相对于球体质量的量都是无限小的,因此可以得出,为了能够凭借自己的阻力从物体夺走其运动的一个无限小的部分,它的对抗速度必须是大小有限的。因此,柔软物质的每一个元素都以一种具有速度有限尺度的努力给砸入物体提供了阻力。等等。
这样,我们已经完成了自己的事情,鉴于它所指向的题材,只要阐述符合这一大胆妄为,这件事情就是足够大的。我自夸特别就主题而言,可以说达到了一种无可争议的确定性。就我自认为拥有的这种优越性而言,如果不是事先考虑到我的债主们的博学和明见,我是不会结束当前的论文的。按照笛卡尔学派的机敏努力,不难以数学防止平方测算的混乱;而按照莱布尼茨学派的巧妙安排,在自然界中不可能没有平方测算。对这两个极端界限的认识必然规定双方的真理共同归属的那个点。发现这个点,一点也不需要巨大的洞察力,它只需要稍稍去掉党派的激情,需要心灵倾向的短暂平衡,这样的话,不舒服的感觉立刻就被排除了。尽管我成功地在莱布尼茨先生的事情上发现了一些失误,我在这里也依然是这位伟大人物的负债者,因为如果没有我们应当归功于这位不朽发明者的杰出的连续律的导线,我将一事无成;连续律是找到走出这一迷宫的出路的惟一方法。简而言之,尽管事情的结果最有利于我,但留给我的荣耀份额却是如此之小,使我并不担心,名誉心会如此自贬身价,竟然妒忌我获得这种荣耀。
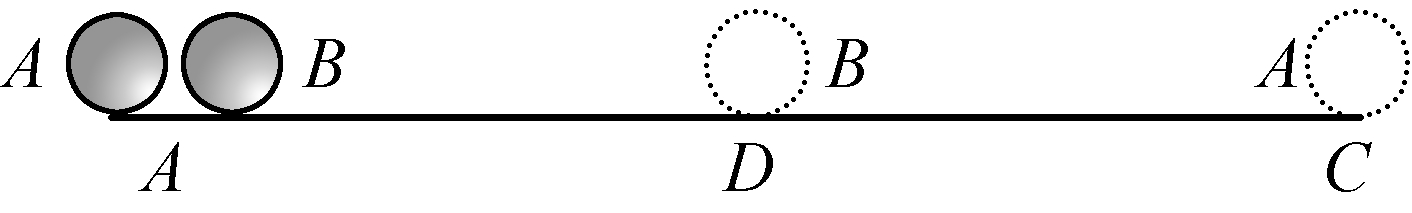
图1
图2
图3
图4
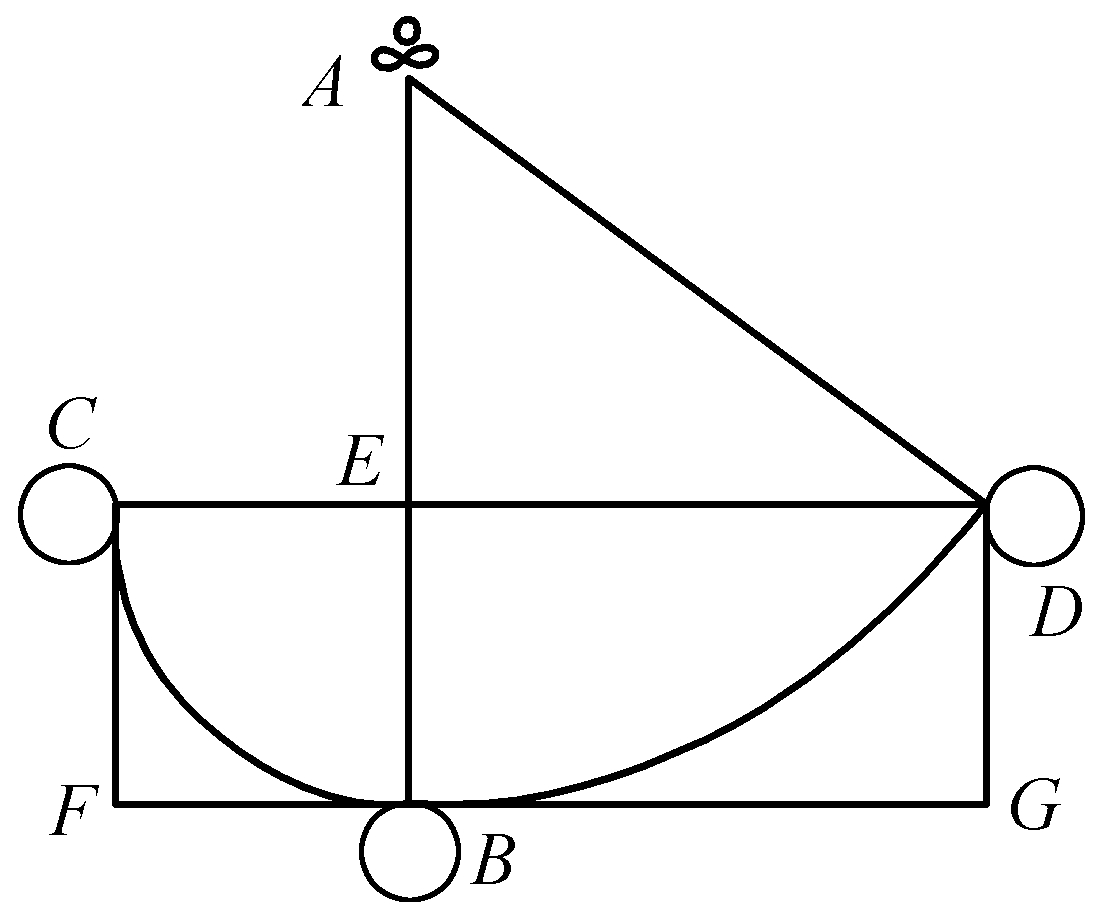
图5
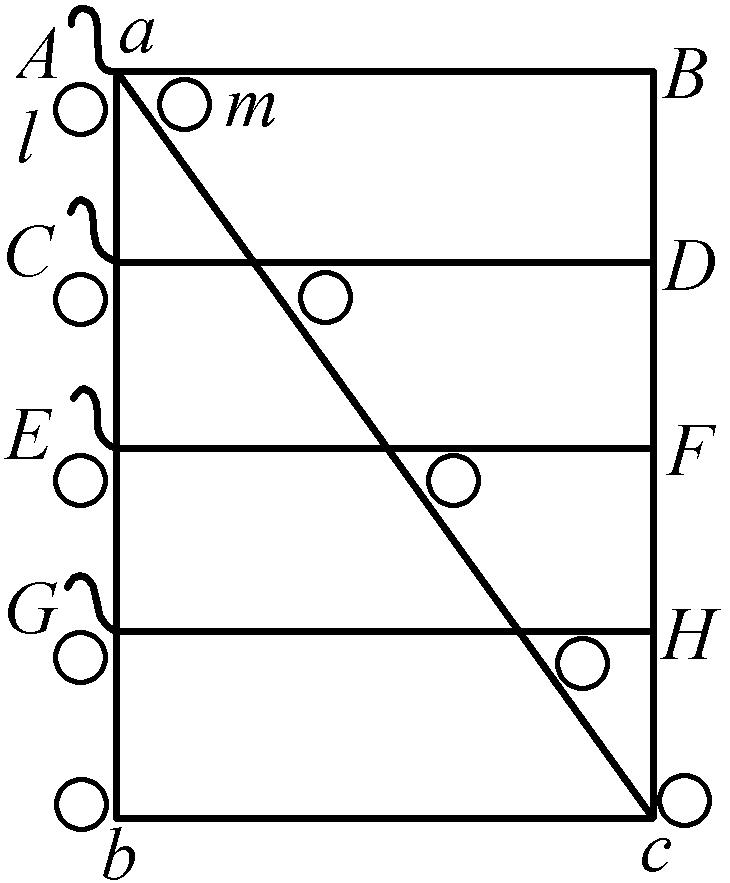
图6
图7
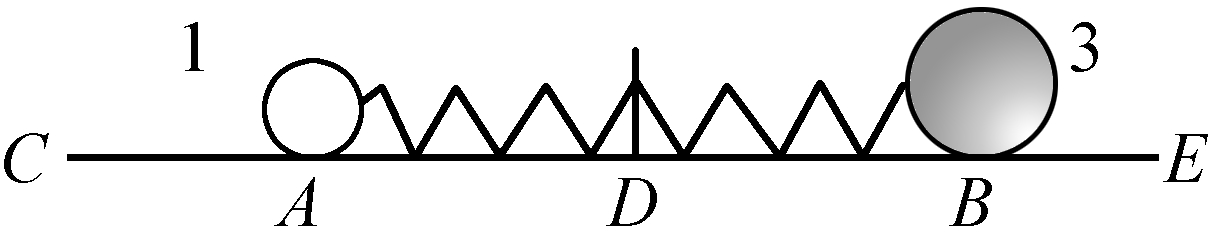
图8
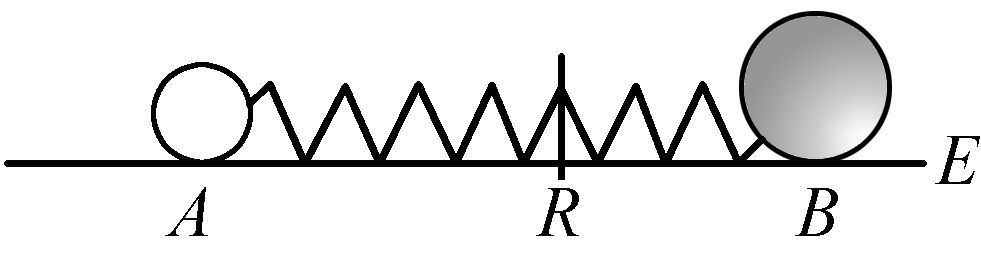
图9
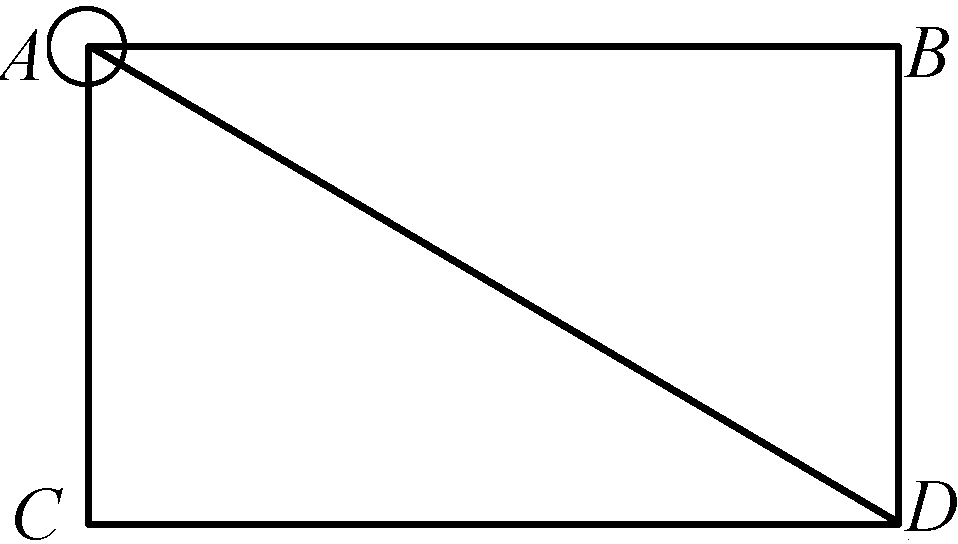
图10
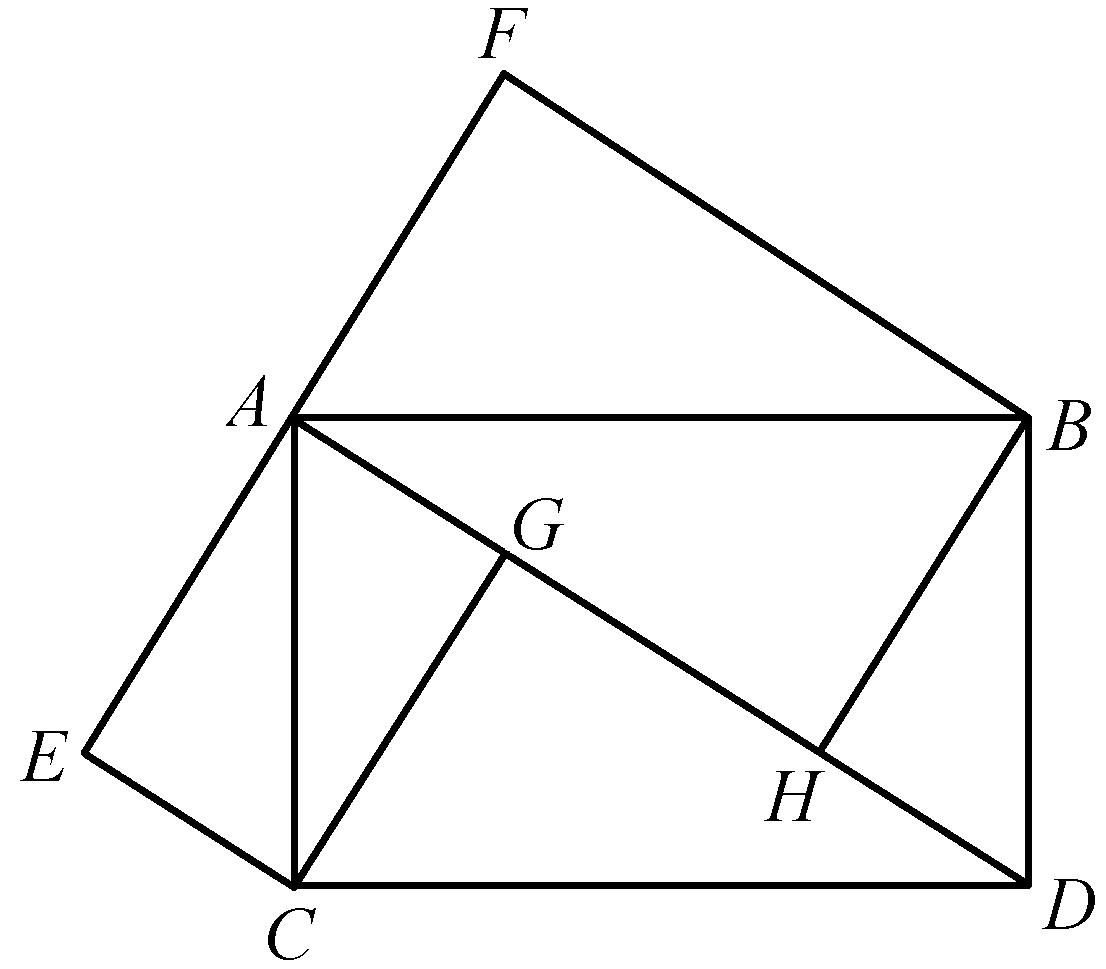
图11
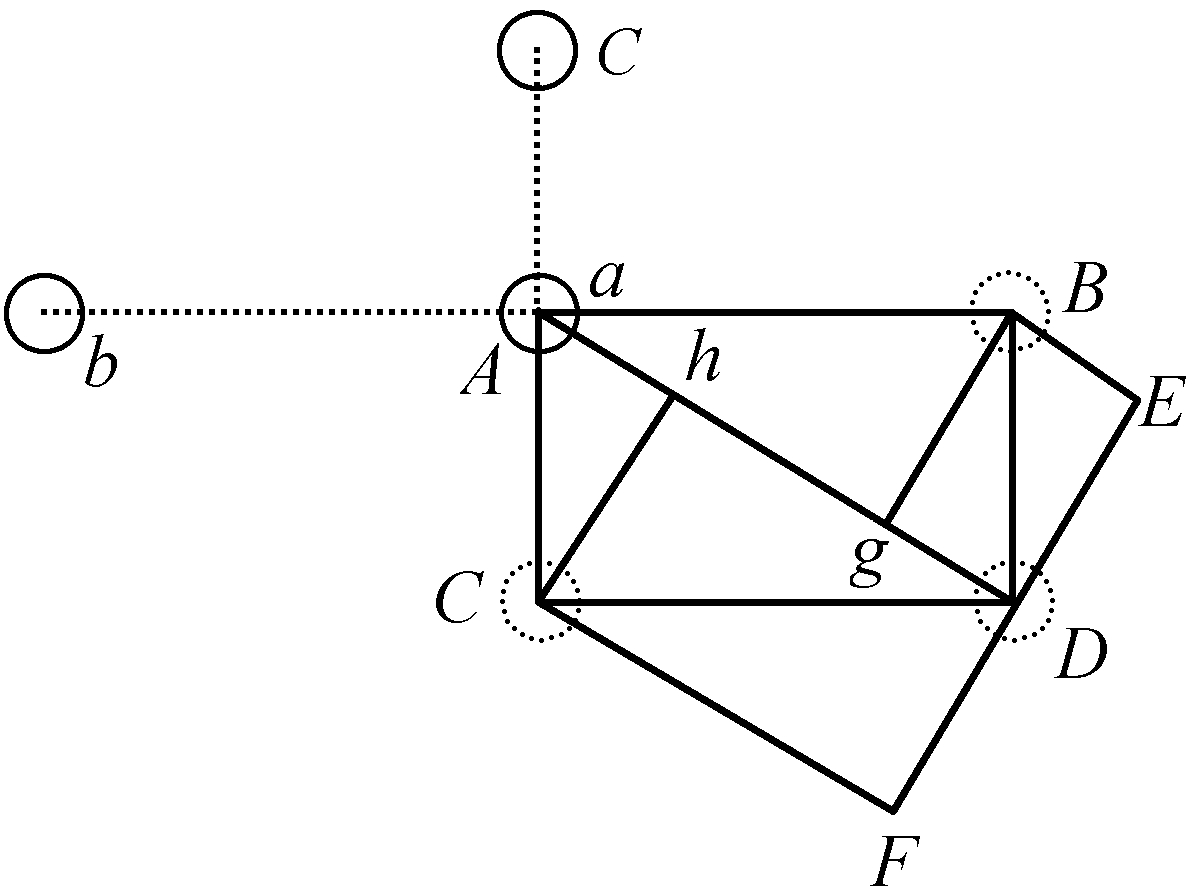
图12
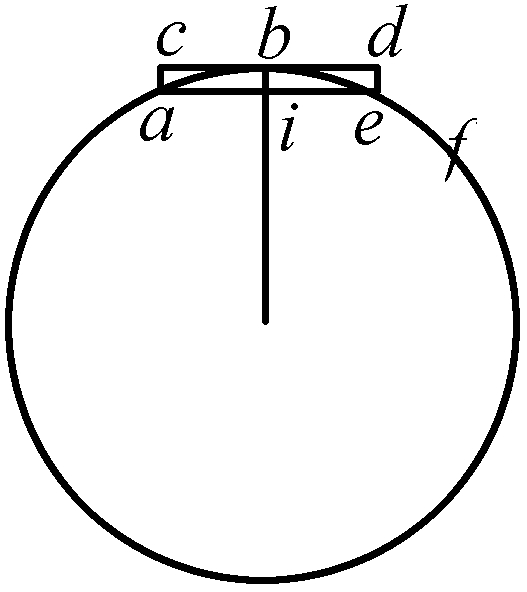
图13
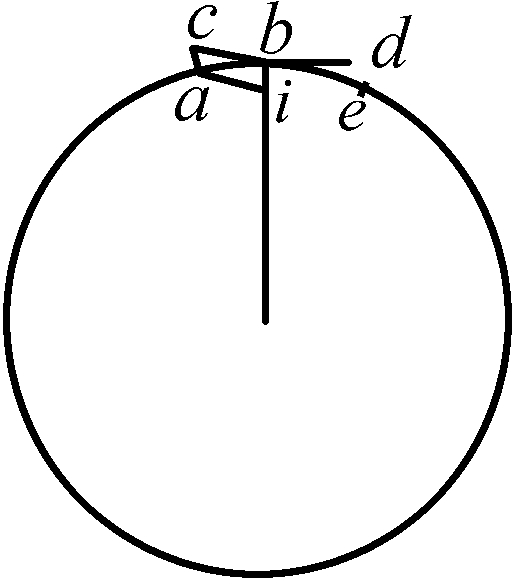
图13(a)
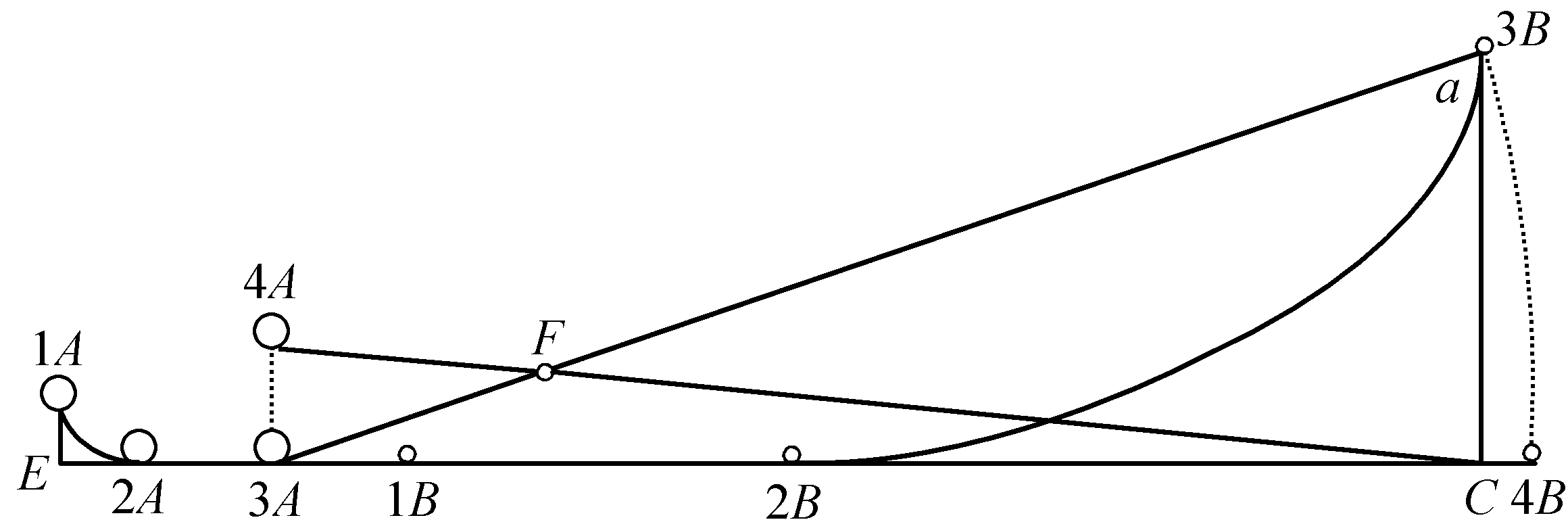
图14
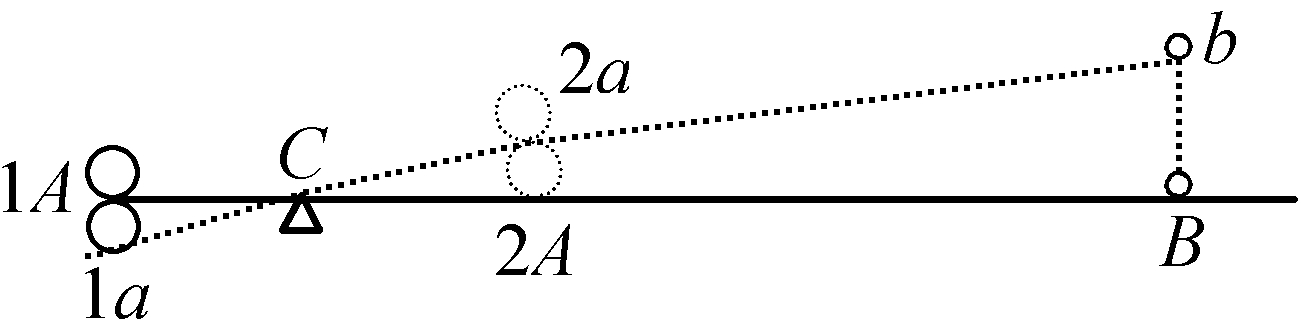
图15
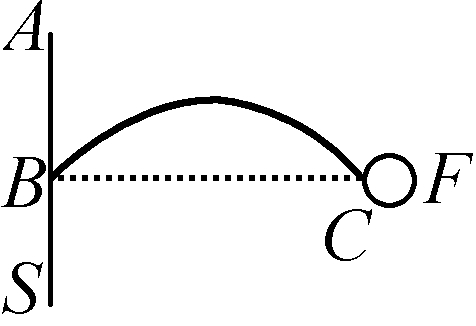
图16
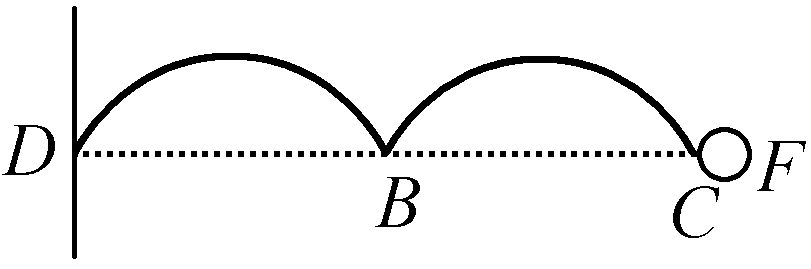
图17
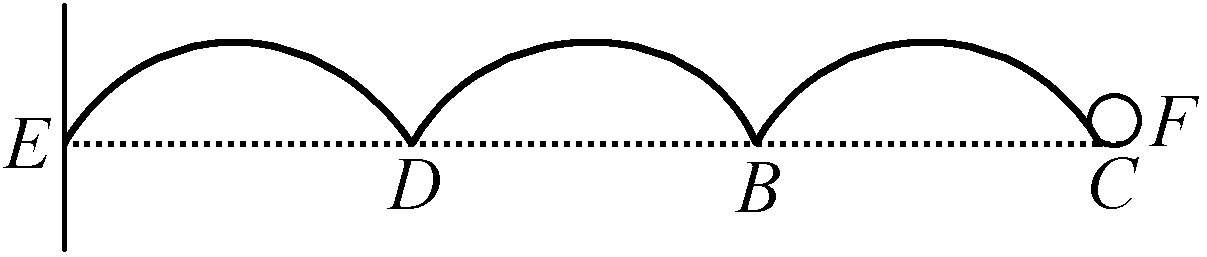
图18
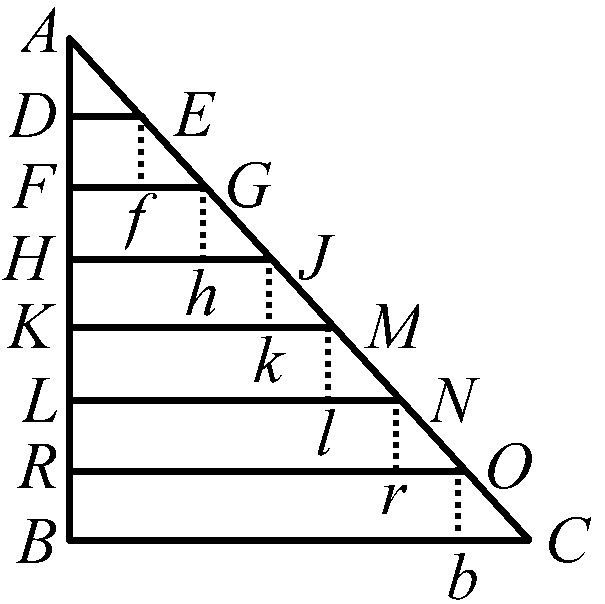
图19
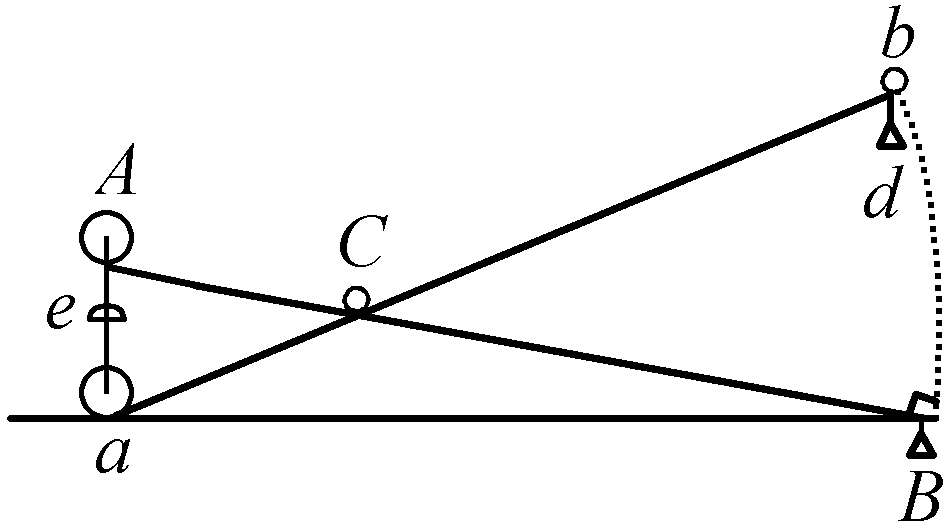
图20
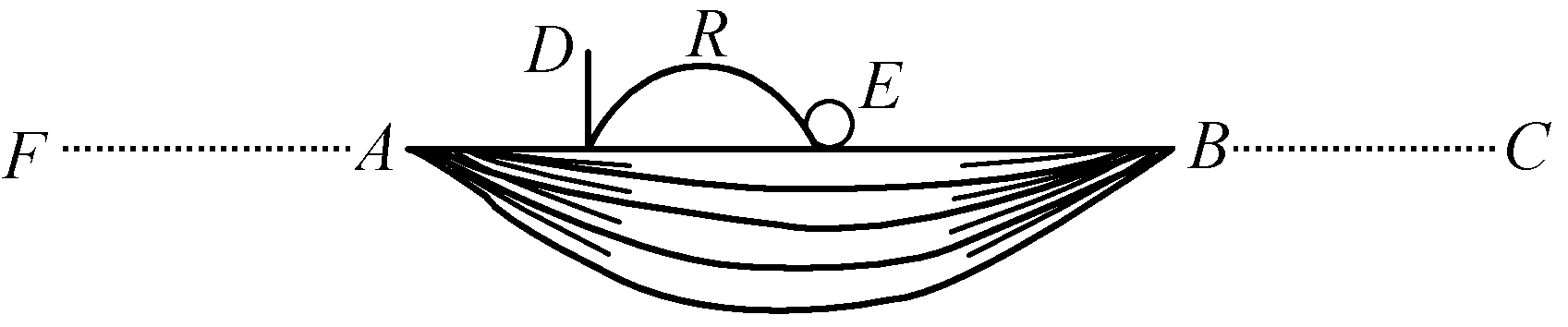
图21
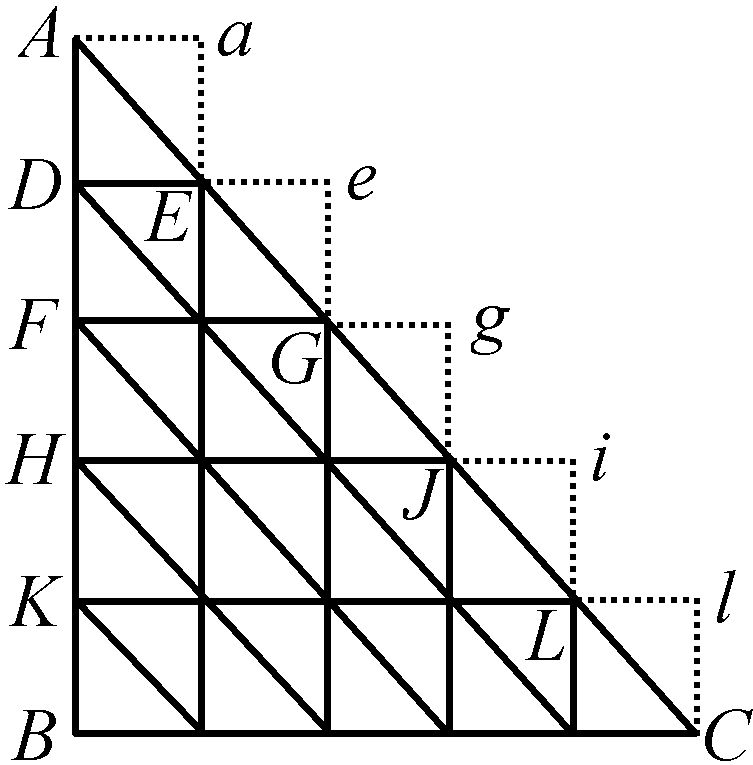
图22
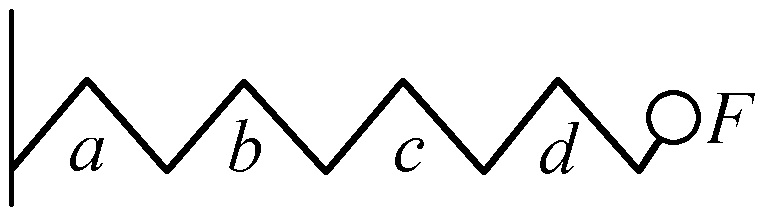
图23
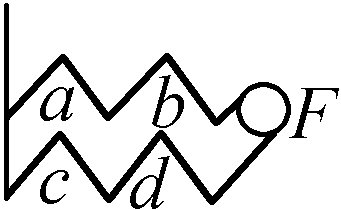
图24
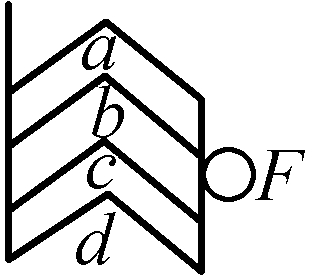
图25
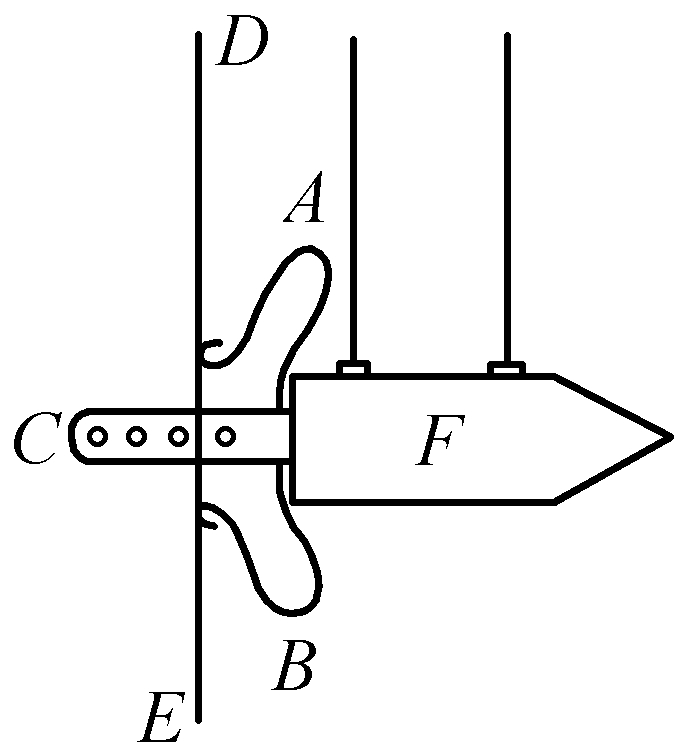
图26
原文收入李秋零主编《康德著作全集》第1卷,作于1747年。