




如1.1节所介绍,网络控制系统所具有的优势使其在实时分布式控制领域得到广泛应用。然而,受网络通信带宽的限制,数据在通过网络传输之前需要进行量化和编码。量化将产生量化误差,量化误差对系统的稳定性及系统性能均有影响。这样就产生了量化控制领域的两个基本研究方向:一个方向是确定保证系统稳定的最小码率,另一个方向是设计适当的编码方案使得在量化误差存在的条件下保证系统稳定。
在确定最小码率方面,研究人员已经获得了一些有价值的理论结果
[9-11,19,47,73]
。其中最基本、最重要的结果是建立了保证系统稳定的条件下,系统动态演化速度与信道传输率(码率)之间的关系。如文献[11]给出了在(
A
,
B
)是可稳定的条件下,线性时不变离散系统式(1-1)可渐进稳定的充要条件是码率
R
满足
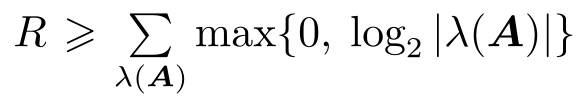 。文献[1,9-10,18-19,47,73]也给出了系统在不同条件下保持稳定时最小码率应满足的条件。这些结果基于以下假设:信道无噪声、无时延且编码器/解码器可获得系统状态和控制输入量的过去和当前的信息。
。文献[1,9-10,18-19,47,73]也给出了系统在不同条件下保持稳定时最小码率应满足的条件。这些结果基于以下假设:信道无噪声、无时延且编码器/解码器可获得系统状态和控制输入量的过去和当前的信息。
在实际应用中,编码器/解码器可获得系统状态和控制输入量的过去和当前的信息这一条件是十分苛刻的。例如,在编码/解码时,如果编码器需要当前时刻的控制量,则需要在控制器与编码器之间另设专线,这样实现起来必然增加系统成本,并且维护不方便。另外,编码器/解码器可获得系统状态和控制量的过去信息意味着每个编码器/解码器要拥有相当大的存储容量,这给实际应用带来困难。显然只使用系统当前状态或输出信息的编码器/解码器是十分理想的。因此在编码器/解码器只使用系统当前状态或输出信息的条件下,研究保证量化控制系统稳定的编码方案设计问题是非常有意义的。
在这方面,已有的编码方案设计多采用均匀量化方法(Uniform Quantiza-tion)或对数量化方法(Logarithmic Quantization),以及它们的改进方法(见文献[19-21,25-26,47,67-68])。Liberzon及其合作者利用均匀量化方法在这方面做了很多工作,如在文献[26]中利用均匀量化方法和Zooming-in/Zooming-out技术,设计编码/解码方案,保证具有任意初始条件下无噪声离散线性系统的稳定性;在文献[20]中考虑保证带有界干扰的离散线性系统输入—输出稳定(Input-to-State Stabilization)的编码方案设计问题。国内学者在这方面也做了很多工作,例如,文献[74-75]利用均匀量化方法研究网络系统 H ∞ 量化控制问题,文献[76]获得时滞依赖网络控制系统的时滞上界和均匀量化状态反馈控制器增益,文献[77]考虑不确定大系统的状态量化分散反馈镇定问题,文献[78]考虑量化反馈控制系统渐进稳定性问题。另外,Elia和Mitter提出并利用对数量化方法(Logarithmic Quantization)设计编码方案保证单输入离散系统稳定 [21] 。文献[25]将文献[21]的结果推广到多输入多输出系统。文献[68]又对文献[25]进行了改进,减小设计的保守性。国内在对数量化方法研究方面,文献[79]研究多输入多输出线性离散系统采用对数量化方法的 H ∞ 滤波器设计问题,文献[80]研究一类非线性网络控制系统的量化保成本控制问题,文献[81]考虑一类非线性网络化系统的状态量化 H ∞ 控制。
采用均匀量化方法或对数量化方法设计的编码方案向实用化方向迈进了一步,因为这样的编码方案只需要系统的当前状态信息或输出信息。但应该注意到,对采用均匀量化方法设计的编码方案,量化器参数的选取和系统稳定性分析相对复杂,并且编码方案与控制器是孤立地设计的,而没有将编码方案设计与控制器设计两者很好地结合起来,这样就无法从整体上考虑系统的通信性能和控制性能。对于采用对数量化方法设计的编码方案,量化区域越接近原点,量化分割将越来越密集,因此这种编码方案所需码率不能是固定且有限的。这意味着在实际应用中将受到限制。
综上所述,从实际应用角度出发,迫切需要设计一种新的编码方案。这种编码方案能克服上述两种编码方案的缺点。针对实际网络控制系统的有限带宽,新编码方案要求必须使用有限码率。为了应用方便,编码方案所用的码率应是固定的,而不是时变的。另外,理解信息理论与控制理论的相互关系对量化控制系统的设计是很重要的。在设计量化控制系统时,应将编码方案设计与控制器设计紧密结合起来,而不是孤立地设计。只有将编码方案设计与控制器设计结合起来,才能从整体上考虑系统的通信性能和控制性能以及两者之间的折中。为此本书提出基于球极坐标的编码方案,并在这种编码方案设计及具体应用方面展开研究。