




本书从无噪声信道和噪声信道两个方面介绍在网络控制系统背景下,量化控制系统的主要研究结果。
1)确定性系统
先介绍确定性系统。信号要通过通信网络进行传输,必须经过编码/解码过程,这样就产生量化误差。在控制理论中,量化误差常被看作加性白噪声。如果量化器分辨率高,这种方法是可行的;但如果量化器分辨率低且开环系统不稳定,这种方法就失效了。文献[8,12]指出,对于一个给定的系统,存在一个与该系统参数有关的信道码率,如果实际信道码率低于这个码率,则不存在任何量化方法和控制方法使得系统稳定。文献[16]指出,将量化误差看作加性白噪声,不能揭示以下事实:特征值小于2的无噪声不稳定系统可用无记忆的状态量化方法渐进稳定到原点,但当特征值大于2时,系统状态轨迹就会产生混沌现象。这个现象表明信道容量小会严重影响系统控制性能,因此在设计量化控制系统时,控制问题和通信问题应该同时考虑,而不能孤立地研究。
关于保证系统稳定的最小信道码率的研究最早出现在文献[12]中,一个不稳定的一阶系统(| a |>1),如果采用无记忆量化器保持系统状态有界,当且仅当信道码率大于log 2 | a |时成立,这是码率理论的第一个结果。随后,文献[17]获得保证自回归滑动平均系统的渐进稳定的最小信道码率。文献[1,9,11,18]用不同的方法得到线性系统的最小信道码率。下面我们介绍文献[11]的结果,文献[11]推广了文献[12]的思想。
文献[11]考虑的无噪声信道系统如图1-2所示。信道每次能传输2 R 个符号,即码率为 R 。考虑下面的离散定常系统:

这里 x t ∈R d 是系统状态, u t ∈R m 是控制输入, y t ∈R l 是系统输出, A 、 B 、 C 是适当维数的矩阵。
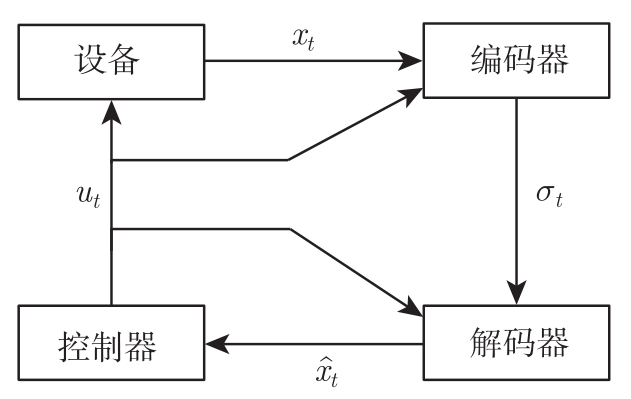
图1-2 文献[11]考虑的无噪声信道系统
定理1.1 [11] 假设( A , B )是可稳定的,系统式(1-1)可渐进稳定的充分必要条件是码率 R 满足
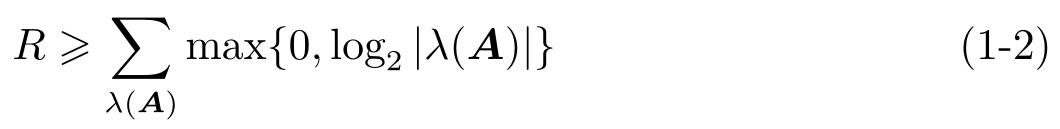
这里 λ ( A )表示 A 的特征值。
这个定理的重要性在于它揭示了码率与系统动态的关系,即如果系统有较快的动态( A 的特征值较大),则码率必须足够大以克服系统动态的影响。文献[11]同时证明在系统式(1-1)有加性白噪声条件下,定理1.1仍成立。
一些文献采用Zooming-in/Zooming-out方法获得系统的输入—状态稳定或渐进稳定。Zooming-in/Zooming-out方法的思想是动态调整量化器的量化范围,当系统状态接近目标点时,增加量化器等级数;当系统状态远离目标点时,减小量化器等级数。从直觉上讲,当系统状态接近目标点时,量化器的分辨率应高些;当系统状态远离目标点时,量化器的分辨率应低些。
在Zooming-in/Zooming-out方法与无记忆量化器相结合方面:文献[2]研究具有未知但有界干扰 ω 的系统
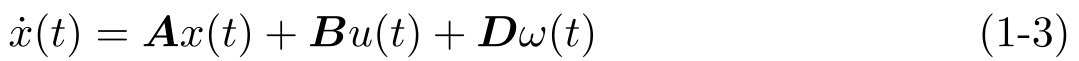
利用Zooming-in/Zooming-out方法设计编码方案保证系统输入—状态稳定(Input-to-State Stability),即满足
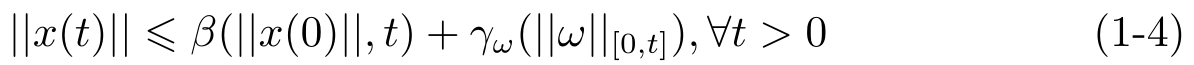
这里 γ ω 是 K ∞ 类函数, β 是 K L ∞ 类函数。文献[19]进一步发展了文献[2]的思想,提出时间采样方法,这种方法基于对轨迹的分析,并利用闭环混杂系统的串级结构。时间采样方法对时延具有鲁棒性。文献[20]在文献[2]基础上,进一步给出了Zooming-in/Zooming-out量化控制方法,不仅在未知干扰界条件下,可以获得系统的Input-to-State稳定性,而且在干扰为0的条件下码率可以任意接近最小码率。文献[21]指出,如果不限制量化器等级数,相对于二次Lyapunov函数,保证系统稳定的最有效量化器是对数量化器。文献[22-24]考虑在给定量化器等级数条件下,保证系统吸引性的对数量化器和一致量化器设计方法。文献[25]采用扇区界方法研究采用对数量化器的系统,保证系统二次稳定性和 H 2 / H ∞ 性能指标。文献[26-28]采用Zooming-in/Zooming-out方法,在允许量化器和编码器有记忆的条件下,获得系统的渐进稳定。文献[29]利用已有的Markov链的稳定结果,研究在无噪声信道条件下,具有高斯噪声的离散线性系统的二阶矩稳定性问题。文献[30]在控制器事先设计好的前提下,给出了系统信噪比与平均信道码率之间的约束关系。文献[31]利用文献[30]的结果,在保证给定系统性能的前提下,分别给出最小平均码率和信噪比的界。
在鲁棒性方面,文献[32]研究了在有限信道码率和一类信源(信源不确定性)条件下,获得系统可观性和稳定性的必要条件。给出信源类熵(Entropy for a Class of Sources)的概念(定义为在一类信源中,香农熵的最大值),并给出信源类的香农信息传输理论[为保证可靠通信,信道容量应大于或等于最小—最大率失真(Mini-Max Rate Distortion)]。文献[33]在加性白噪声信道和信源不确定性条件下,研究系统均方可观性和鲁棒性问题。文献[34]考虑不确定离散系统在信道容量受限条件下的鲁棒性问题。文献[35]考虑码率变化的鲁棒量化问题,证明如果无噪声连续线性系统在无记忆条件下采用量化控制,则对数据包传输时间变化最鲁棒的方法是小采样时间的二进制量化。文献[1,11]考虑存在有界干扰的系统稳定性。
文献[2,36-42]将上述方法推广到非线性系统。文献[2,40]应用Zooming方法将Input-to-State稳定的非线性系统转变为渐进稳定系统。文献[42]将一类稳定非线性系统的码率条件与拓扑反馈熵(Topological Feedback Entropy)概念联系起来,这个概念推广了已有的无输入非线性系统的拓扑熵概念。文献[41]将对数量化方法推广到仿射非线性系统。文献[39]获得保证具有前馈结构的非线性系统稳定的码率界。
2)随机系统
以上介绍的结果都针对确定性系统,文献[43-49]考虑了随机系统。文献[43]考虑部分可观测线性高斯系统在码率受限条件下保二次型代价控制问题,表明如果测量信号通过最小方差滤波器,且选择滤波器的输出为量化器的输入,则编码器与控制器可分别设计(分离原理)。文献[48]在更一般条件下考虑线性高斯系统的分离原理和确定性等价原理,给出加性高斯白噪声信道和无噪声信道的码率失真的理论下界。文献[49]给出在线性定常控制器条件下,使用一致量化器和变长编码,保证单输入单输出线性定常高斯系统稳定的充要条件。文献[47]考虑具有非高斯噪声的线性系统的均方稳定问题,得到时间渐进均方状态范数(Time-Asymptotic Mean Square State Norm)的下界。这个下界表明当码率接近系统的本征熵率(Intrinsic Entropy Rate) H 时,不管何种编码方案和控制方案,状态的均方值都将变得任意大。文献[44]也有类似的结果,显示当反馈信道的香农容量 C 向 H 降低时,控制器控制系统输入功率谱的能力降低。
一些文献考虑噪声信道条件下的量化控制,如二进制擦除信道 [9,50-51] 、二进制对称信道 [45,52-53] 、截断信道 [54] 等。如果信道是噪声信道,系统的稳定性问题将变得非常复杂,结果依赖稳定性的不同概念及编码器是否获得关于信道的边信息(Side-Information)。一般不能采用香农容量 C 作为控制系统中衡量信道的指标。尽管 C>H 是在无信道边信息条件下系统几乎处处渐进稳定的充分必要条件,但不是其他稳定性的充分必要条件,如均方稳定性。原因是在香农编码理论中,以接近传输率 C 进行可靠传输是以增加编码时延为代价的,然而随着时延增加,系统状态将更远离原点,因此需要更多的信息稳定系统。但如果信道是加性高斯白噪声信道,且系统是线性高斯系统,则 C>H 仍然是系统均方稳定的充要条件 [48,52,55] 。文献[52]引入任意时间容量(Anytime Capacity)概念,指出如果控制目标是矩稳定的,则任意时间容量才是噪声信道的度量标准,而不是香农容量。然而,不像香农容量,任意时间容量没有简单的表达式便于计算。
当系统的反馈回路包括噪声信道时(如图1-2所示),渐进稳定的定义必须做适当的修改,因为确定性系统的渐进稳定的定义不再适用于具有噪声信道的系统。我们介绍两种稳定性:几乎处处稳定和 m 阶矩稳定。
1)几乎处处稳定
定义1.1 [51] 如果存在编码器/解码器和控制器使得|| x t ||几乎处处趋于0,则系统式(1-1)是几乎处处稳定的。
定义1.2 [56] 给定信道{ P ( W t | V t ,W t -1 )},在[0, T ]时间上的香农容量定义为
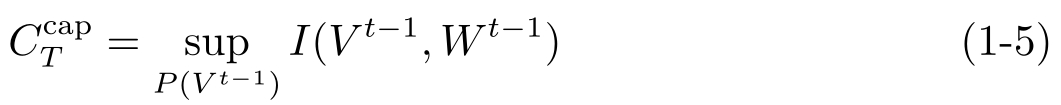
这里 I (·,·)是互信息, V 是输入字符集, V t ={ V 1 , V 2 ,…, V t }, W 是输出字符集, W t -1 ={ W 0 , W 1 , W 2 ,…, W t -1 }。
对于定义1.1,不等式(1-2)给出的码率界不再有效,需要一个新的条件保证系统几乎处处稳定。
确定性信道与随机信道的差别在于:在(0,
T
)时间内,无噪声信道的信道容量是
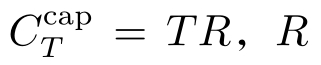 是码率;而对于噪声信道,不同的噪声信道有不同的信道容量。时延信道的信道容量
是码率;而对于噪声信道,不同的噪声信道有不同的信道容量。时延信道的信道容量
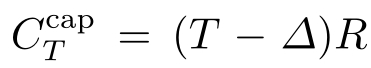 ,
∆
是时延;对于擦除概率为
α
的擦除信道,信道容量
,
∆
是时延;对于擦除概率为
α
的擦除信道,信道容量
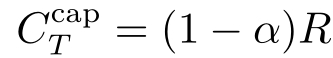 ;无记忆高斯信道的信道容量
;无记忆高斯信道的信道容量
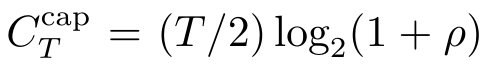 ,
ρ
为噪声功率。文献[51]在香农容量基础上给出保证系统几乎处处稳定的必要条件。这个条件与噪声信道的类型无关,因为使用极限
,
ρ
为噪声功率。文献[51]在香农容量基础上给出保证系统几乎处处稳定的必要条件。这个条件与噪声信道的类型无关,因为使用极限
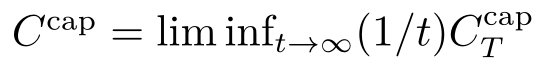 代替与信道类型有关的信道容量
代替与信道类型有关的信道容量
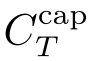 。
。
定理1.2 [51] 对系统式(1-1),在( A , B )是可稳定的条件下,系统几乎处处稳定的必要条件是
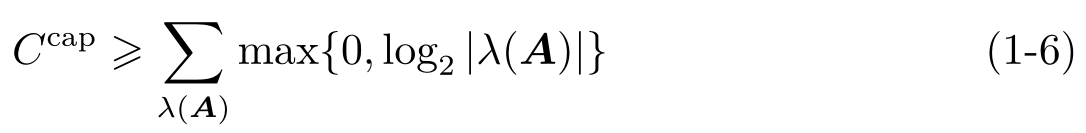
文献[57]考虑有界干扰系统的输入-状态几乎处处稳定问题,给出擦除信道条件下保证系统稳定的丢包条件。
2) m 阶矩稳定
文献[52]引入任意时间容量(Anytime Capacity)概念,指出如果控制目标是矩稳定的,则任意时间容量才是噪声信道的指标,而不是香农容量。考虑下面的一阶系统(见图1-3):
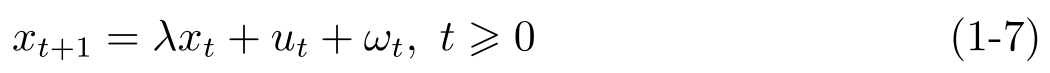
式中,
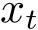 是系统状态,
是系统状态,
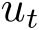 是控制输入,
是控制输入,
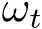 是有界干扰噪声。
是有界干扰噪声。
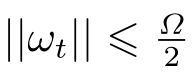 ,假设初始状态
,假设初始状态
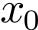 =0。
=0。
定义1.3 [52] 如果存在一个常数 K 使得对于所有 t 满足

系统式(1-7)是 m 阶矩稳定的。
定义1.4 [52] 对于某一常数 K 、任意 d 和任意 t ,信道的 α 任意时间容量 C anytime ( α )是保证式(1-9)成立的信道码率的最小上界:
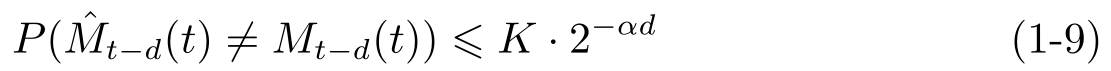
式中,
M
i
(
t
)是编码器
i
时刻收到的
R
位信息,
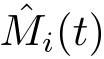 是解码器对
t
时刻信息
i
的最优估计,
d
是时延。
是解码器对
t
时刻信息
i
的最优估计,
d
是时延。
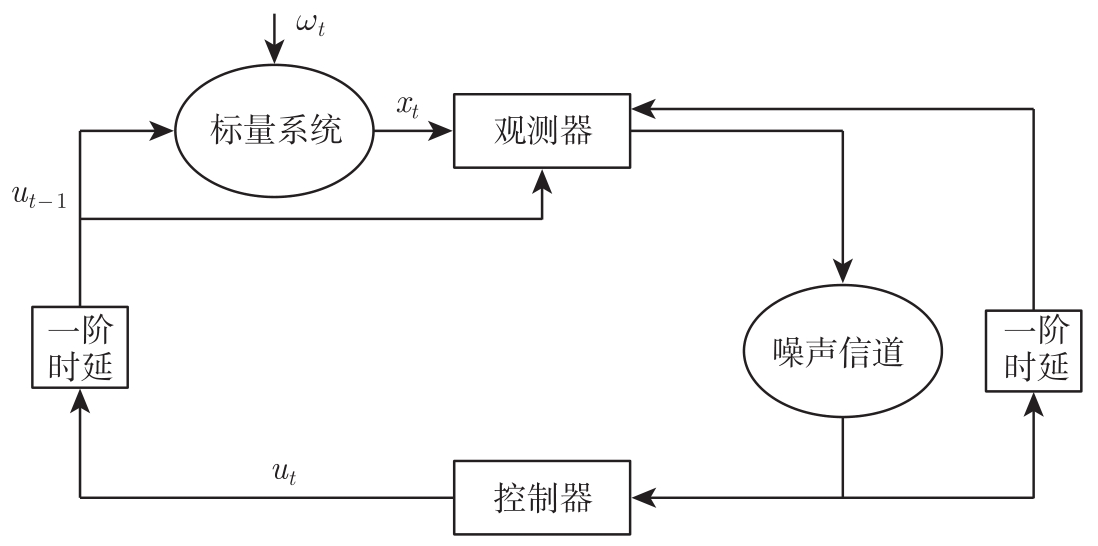
图1-3 文献[52]考虑的系统
定理1.3
[52]
(必要条件):对于给定的噪声信道,如果存在观测器和控制器使得对于噪声
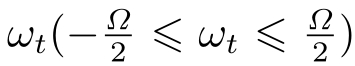 ,系统式(1-3)满足
E
{||
,系统式(1-3)满足
E
{||
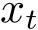 ||
m
}≤
K
,那么带有无噪声反馈信道的信道码率应满足
||
m
}≤
K
,那么带有无噪声反馈信道的信道码率应满足
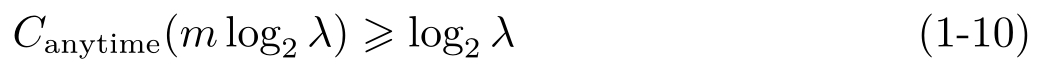
定理1.4 [52] (充分条件):如果带反馈的信道满足 C anytime ( m log 2 λ + ε )≥log 2 λ , ε >0且观测器能准确观测到噪声信道的输出和状态,则系统式(1-3)的状态满足 E {|| x t || m }≤ K 。
不像香农容量,一般来说,任意时间容量没有简单的表达式便于计算。文献[54]考虑更一般的情况,即系统既有外部干扰,参数不确定,又有码率随机变化的信道情况:
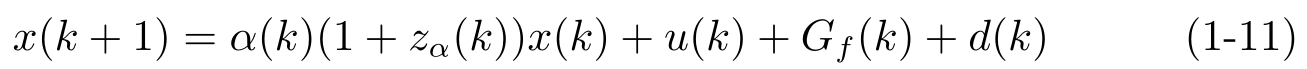
式中, z α ( k )代表 α ( k )的不确定性, G f ( k )代表反馈不确定环节的输出, d ( k )代表有界扰动。
文献[54]指出这种情况下的矩稳定要求平均码率必须满足 C>R + α + β ,这里 C 代表反馈回路中可靠传输的平均码率, R 是与系统矩阵特征值有关的量, α 、 β ≥0分别表示与信道不确定性和系统不确定性有关的量。这表明在系统存在信道不确定性和系统参数不确定性时,仅 C>R 对于系统矩稳定性是不充分的。文献[54]进一步说明, C 越大,系统克服信道不确定性和系统不确定性的能力越强。
文献[58]考虑在擦除信道条件下,保证离散线性时不变系统均方稳定的最小码率问题。文献[59]利用已有的Markov链的稳定结果,研究擦除信道条件下,具有高斯噪声的离散线性系统的二阶矩稳定性问题。同样,文献[60]利用Markov链的稳定结果,考虑在上行信道和下行信道条件下,由布朗运动驱动的连续线性时不变系统的稳定问题。文献[61]考虑具有标量擦除信道(Scalar Erasure Channel)的控制系统,证明在二阶矩意义下,这种信道等价于具有瞬时信噪比约束的白噪声信道。
受经典控制理论中关于系统性能的Bode积分不等式的启发,一些学者研究网络控制系统的“Bode积分不等式” [44] ,给出反馈回路存在信道条件下,系统性能的限制条件,如图1-4所示。
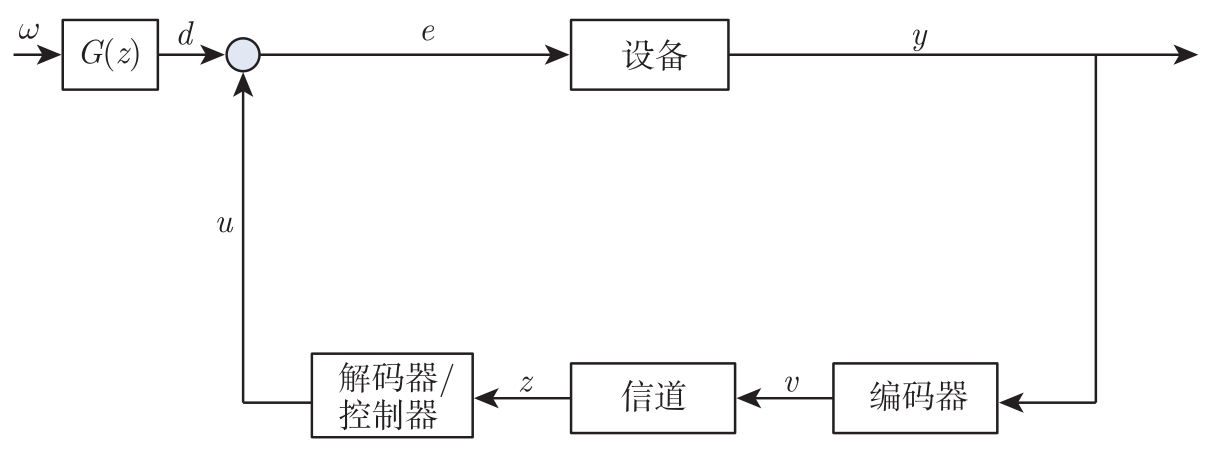
图1-4 文献[44]考虑的系统
文献[44]得到不等式
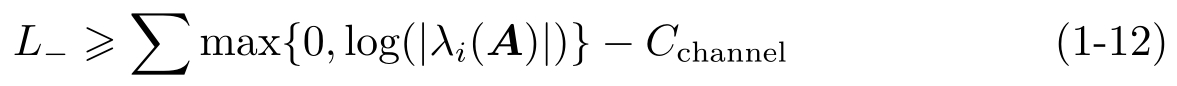
这里 L - 是干扰抑制的度量, A 是系统矩阵, C channel 是信道的香农容量。 L - 是非正数且 L - 越小,对于干扰的抑制程度越大,即 C channel -∑max{0,log(| λ i ( A )|)}决定干扰抑制的基本限制。如果系统稳定, L - 是系统对数灵敏度的积分描述。文献[62]考虑码率受限、时变信道条件下,保证具有任意干扰的线性离散系统稳定性的码率问题。假设信道码率变化较慢,接收器和发送器可通过信道的反馈估计信道的质量,利用通信理论和控制理论的方法给出系统稳定的充分和必要条件。
以上文献所给出的很多结果是在编码器/解码器可获得系统状态和控制输入量的过去和当前的信息条件下获得的。例如,获得保证系统稳定所需码率的严格界就要求编码器/解码器需要知道系统状态和控制输入量的过去和当前的信息,即编码器/解码器有记忆。如果在无记忆或有限记忆条件下,问题将变得复杂。原因是码率与控制器耦合在一起,最小码率与所选择的控制器有关 [11] 。在实际应用中,编码器/解码器可获得系统状态和控制输入量的过去和当前的信息这一条件是十分苛刻的。例如,在编码/解码时,如果编码器需要当前时刻的控制量,则需要在控制器与编码器之间另设一专线(码率无限大的无噪声信道)。这样实现起来必然增加系统成本,并且维护不方便。另外,编码器/解码器可获得系统状态和控制量的过去信息意味着每个编码器/解码器要拥有相当大的存储容量,这给实际应用带来困难。显然只使用系统当前状态或输出信息的编码器/解码器是十分理想的。因此在编码器/解码器只使用系统当前状态或输出信息的条件下,研究保证量化控制系统稳定的编码方案设计问题是十分有意义的,已有一些结果 [19-21,25-26,47,63-68] ,但仍存在一些问题,见1.3节。本书将在这方面展开研究。