5.1 问题描述

考虑下面线性时不变连续系统，系统的传感器与控制器通过无噪声信道连接。

式中， x （ t ）∈R ⁿ 和 u _c （ t ）∈R ^m 分别是系统状态和输入， H 和 W 是适当维数的系统矩阵。首先系统状态 x （ t ）以采样周期 T 被采样，采样值为 x （ k ）= x （ kT ）， k =0，1，2，3，…，然后采样值被编码，通过网络传输后，解码为 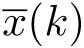。控制器接收到 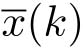后产生控制量 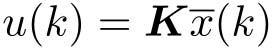，由于网络时延，因此作用到系统的实际控制量为 u _c （ t ），其中， K 为状态反馈增益矩阵。 u _c （ t ）与 u （ k ）的关系为

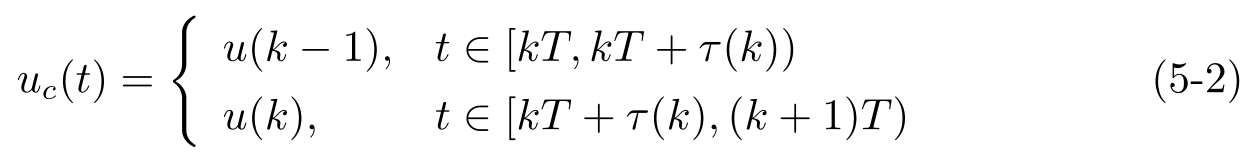
这里 τ （ k ）是传感器到控制器的网络时延。不失一般性，假设初始状态是有界的，不确定参数 τ （ k ）也是有界的，并且满足

式中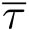， 为上界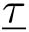， 为下界。系统式（5-1）被离散化为下面的系统

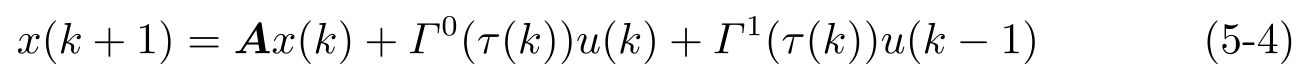
这里 A =e ^Ht ，

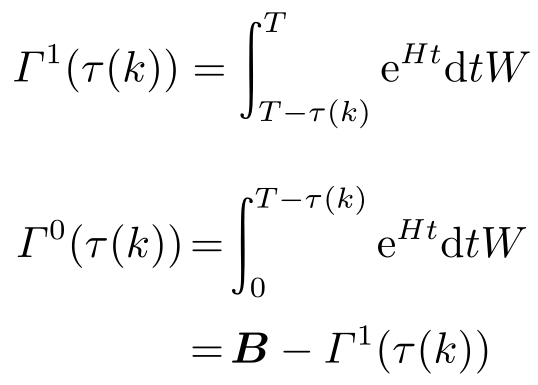
其中

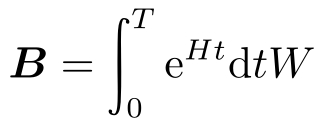
应用状态反馈控制器

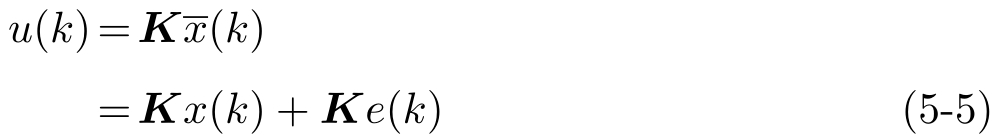
闭环系统为

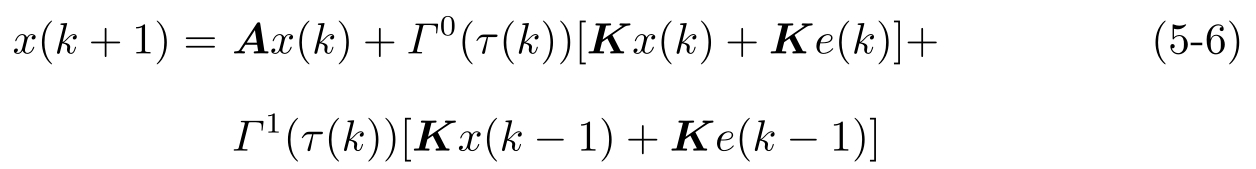
其中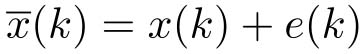， ，量化误差 e （ k ）由编码/解码过程产生。

位于传感器和控制器之间的信道是无噪声信道，可以在每个采样周期内传送一个码字，用 V （ k ）∈ Σ 表示，其中 Σ 表示码字集合（码书）。这样在每个采样周期内，信道可无误差地传送 R =log| Σ |位信息，这里| Σ |表示集合的势。我们考虑具有有限码率信道的网络诱导时延系统的渐进稳定问题。

问题5.1 给定系统矩阵 H 、 W 和初始状态的界，设计球极坐标编码器{ E _k ，k ≥0}[见式（5-7）]，球极坐标解码器{D _k ，k ≥0}[见式（5-8）]，并求信道码率 R =log| Σ |和状态反馈矩阵 K 使得闭环网络时延控制系统式（5-6）渐进稳定。 IbEhkF0NabOTnYi10oXEgfroT3+SC+vc0UusNS0CIyTqvvADxnBer9EQhOcilBOJ