




取
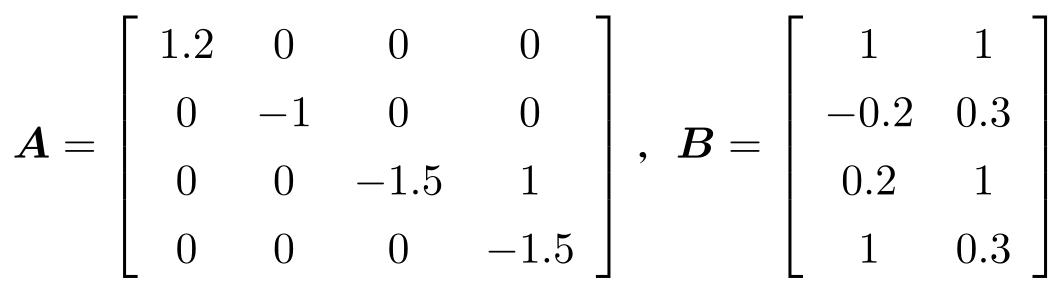
A 有不稳定特征值1.2、-1、-1.5、-1.5,并且( A , B )是可控的。令擦除概率 p =0.15。
对于系统的平均渐进稳定性,用4.4节所给的算法,可得

因此有
 。用Cholesky分解,得到
。用Cholesky分解,得到

满足 Q = P -1 P -T 。
确定量化器(
L
k
,N,a,M
)的参数:取
η
=0.028,
a
=0.002,
M
=182,
N
=436满足式(4-19)和式(4-21),
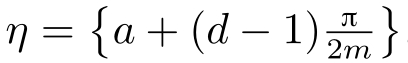 。由式(4-22)可得,码率
R
≥33。图4-2所示为状态响应曲线,其中初始状态
x
(0)=[10,-5,8,-7]
T
,界
。由式(4-22)可得,码率
R
≥33。图4-2所示为状态响应曲线,其中初始状态
x
(0)=[10,-5,8,-7]
T
,界
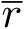 =16。定义
=16。定义

函数
g
(
k
)表示
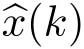 落入支撑球的哪个区域,如图4-3所示。用同样的量化器和控制器,擦除概率
p
=0.1的状态响应曲线和函数
g
(
k
)分别如图4-4和图4-5所示。这表明在大擦除概率条件下设计的量化器和控制器可以在小擦除概率条件下保证系统平均渐进稳定。
落入支撑球的哪个区域,如图4-3所示。用同样的量化器和控制器,擦除概率
p
=0.1的状态响应曲线和函数
g
(
k
)分别如图4-4和图4-5所示。这表明在大擦除概率条件下设计的量化器和控制器可以在小擦除概率条件下保证系统平均渐进稳定。
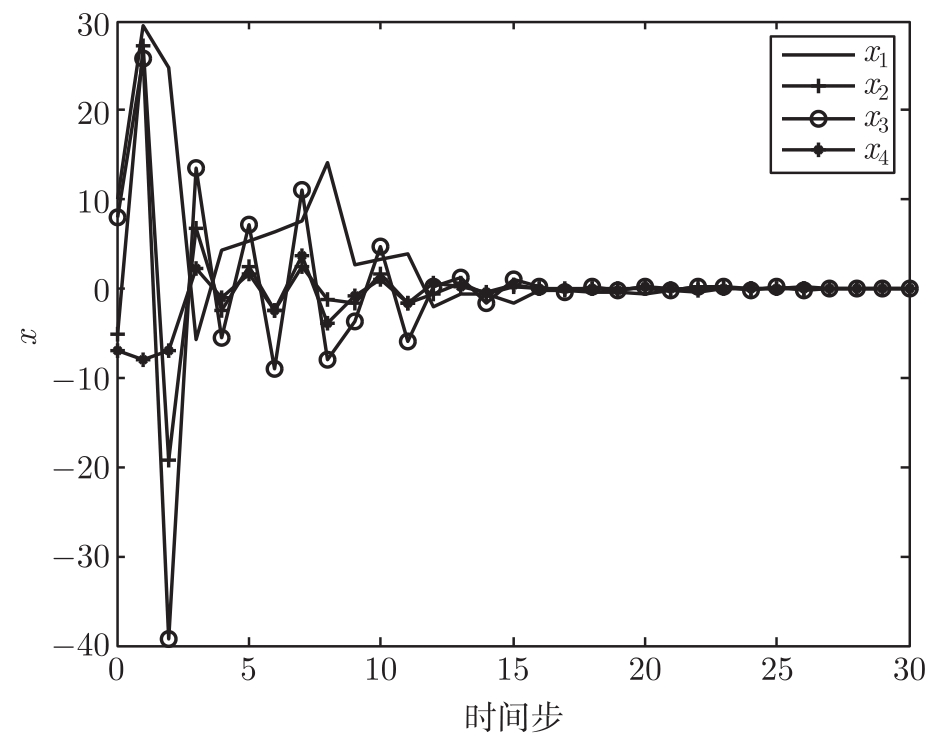
图4-2 当 p =0.15时平均渐进稳定条件下系统状态 x 的响应曲线
类似地,对于几乎处处渐进稳定性,得到
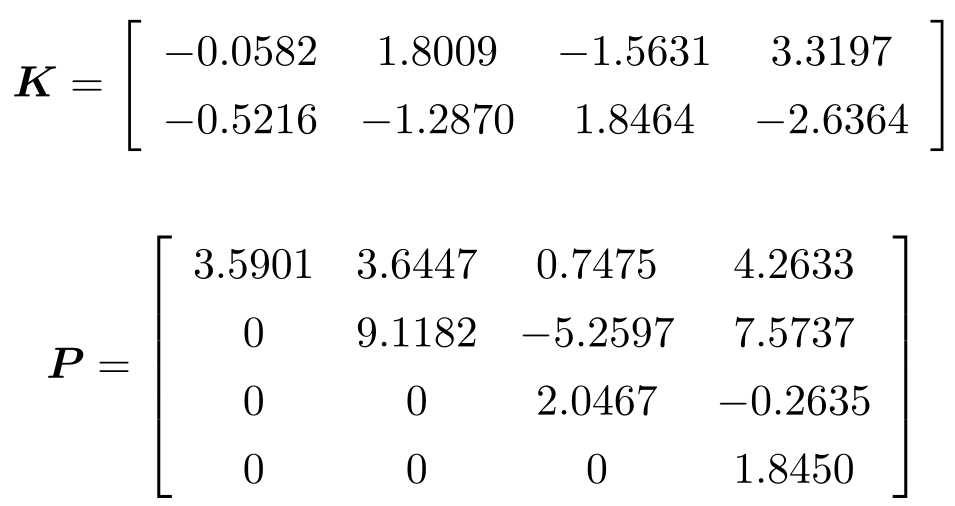
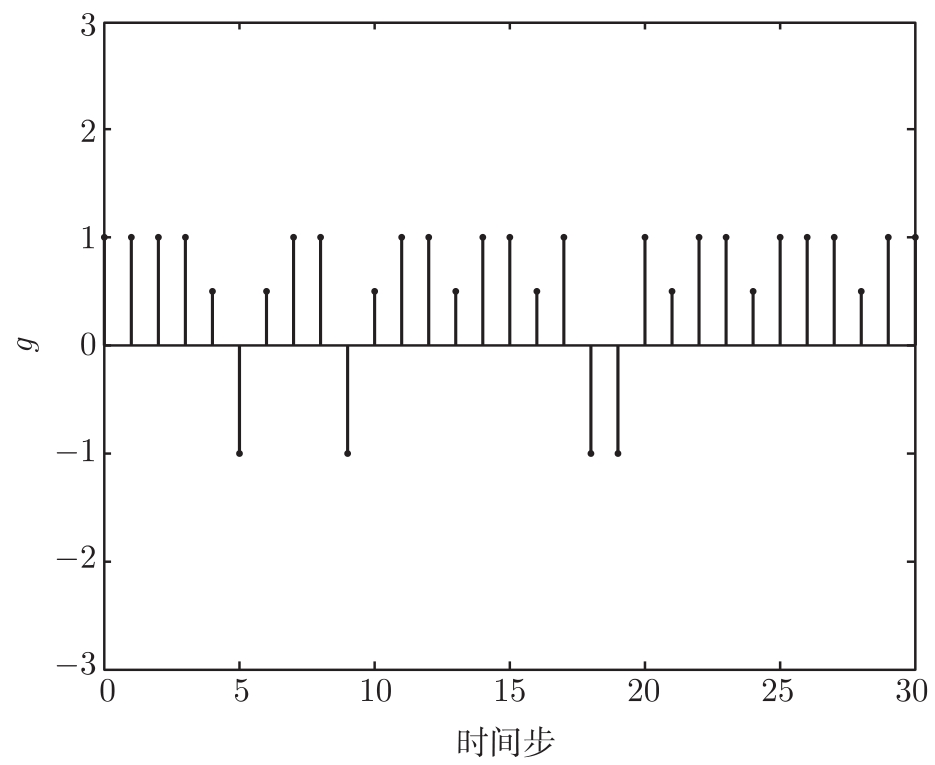
图4-3 当
p
=0.15时平均渐进稳定条件下系统式(4-12)的状态
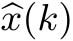 所处的区域
所处的区域
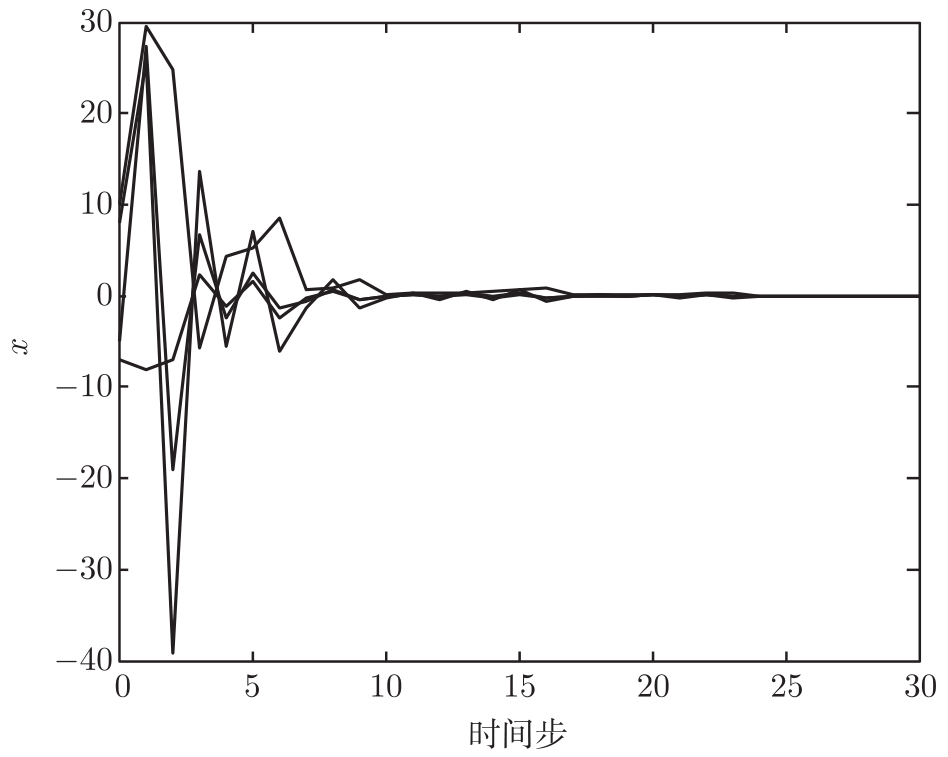
图4-4 当 p =0.1时平均渐进稳定条件下系统状态 x 的响应
确定量化器(
L
k
,N,a,M
)的参数:取
η
=0.0614,
a
=0.007,
M
=87,
N
=152满足式(4-20)和式(4-21),
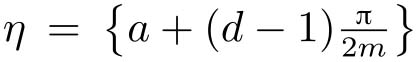 。由式(4-22),码率
R
≥28。图4-6 所示为状态响应曲线,其中初始状态
x
(0)和界
。由式(4-22),码率
R
≥28。图4-6 所示为状态响应曲线,其中初始状态
x
(0)和界
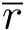 同上。函数
g
(
k
)如图4-7 所示。用同样的量化器和控制器,擦除概率
p
=0.1的状态响应曲线和函数
g
(
k
)分别如图4-8和图4-9 所示。这表明在大擦除概率条件下设计的量化器和控制器可以在小擦除概率条件下保证系统几乎处处渐进稳定。
同上。函数
g
(
k
)如图4-7 所示。用同样的量化器和控制器,擦除概率
p
=0.1的状态响应曲线和函数
g
(
k
)分别如图4-8和图4-9 所示。这表明在大擦除概率条件下设计的量化器和控制器可以在小擦除概率条件下保证系统几乎处处渐进稳定。
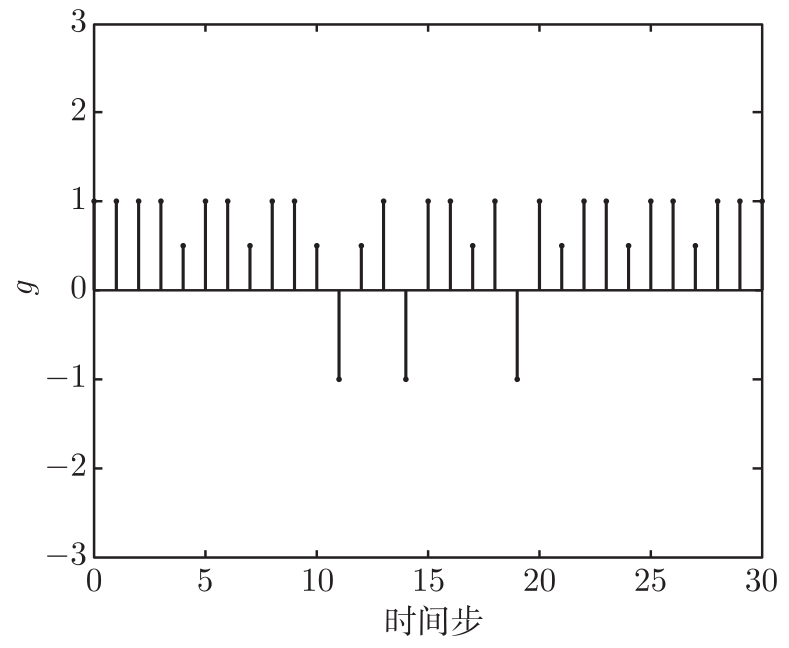
图4-5 当
p
=0.1时平均渐进稳定条件下系统式(4-12)的状态
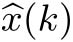 所处的区域
所处的区域
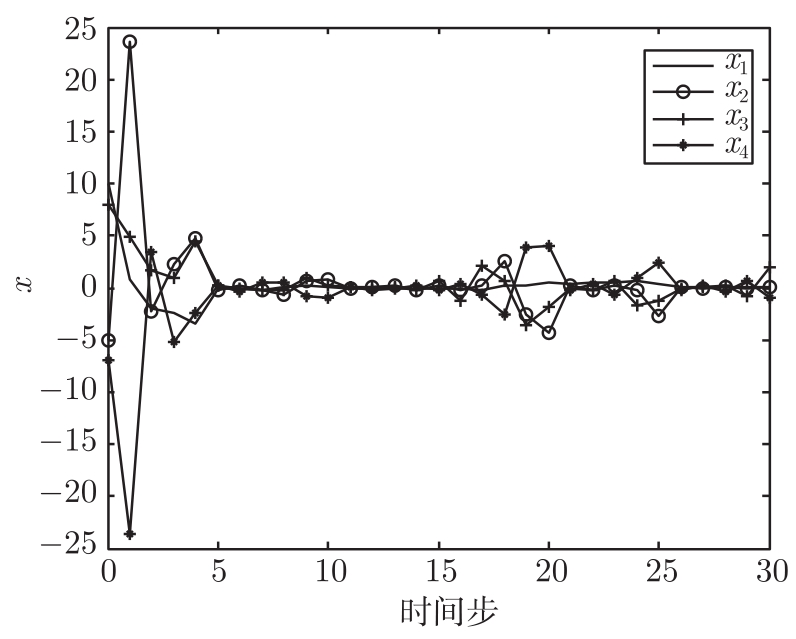
图4-6 当 p =0.15时几乎处处渐进稳定条件下系统状态 x 的响应
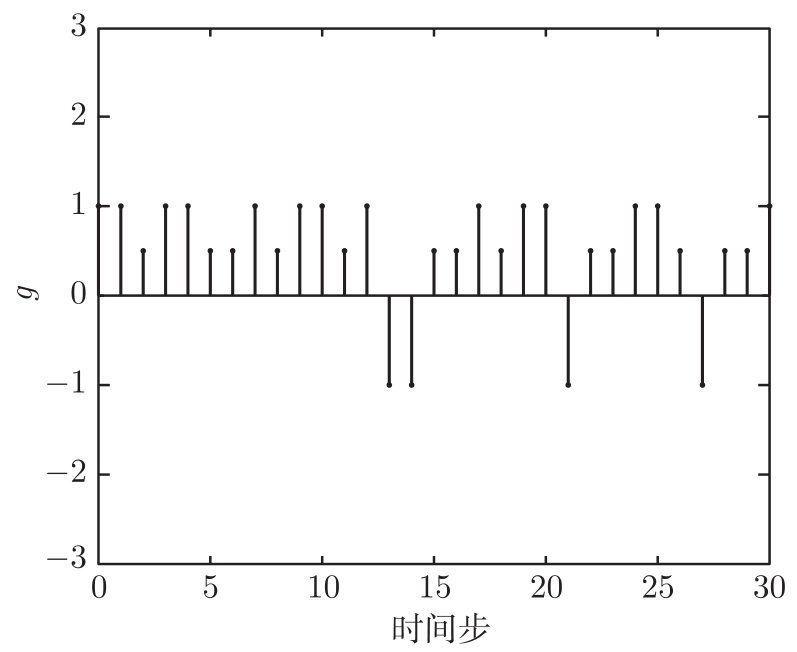
图4-7 当
p
=0.15时几乎处处渐进稳定条件下系统式(4-12)的状态
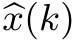 所处的区域
所处的区域
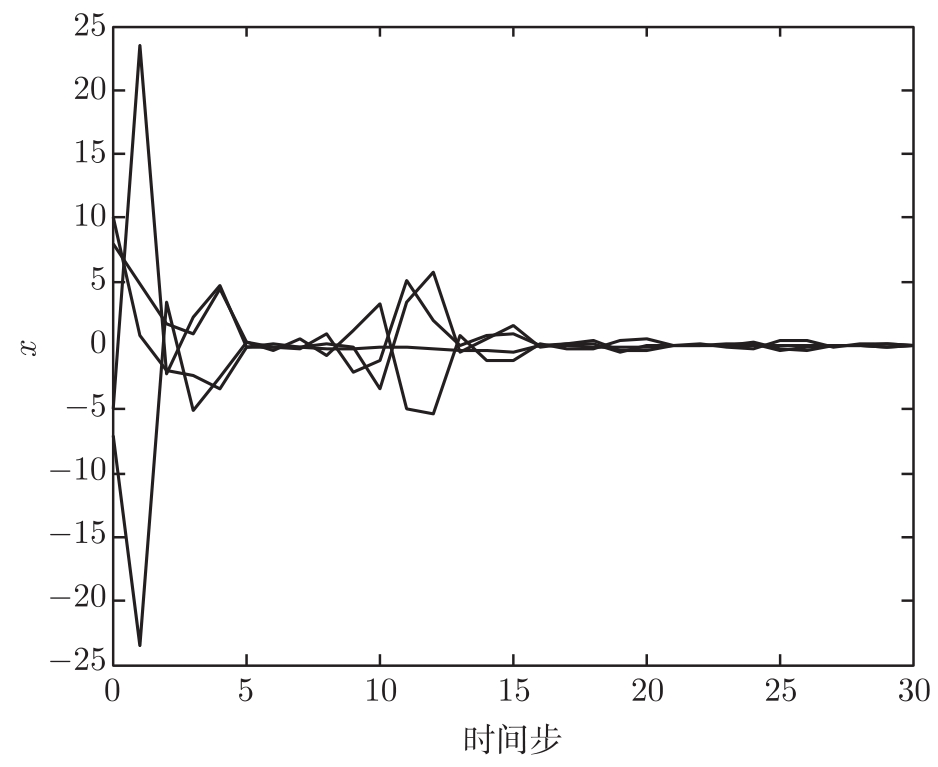
图4-8 当 p =0.1时几乎处处渐进稳定条件下系统状态 x 的响应
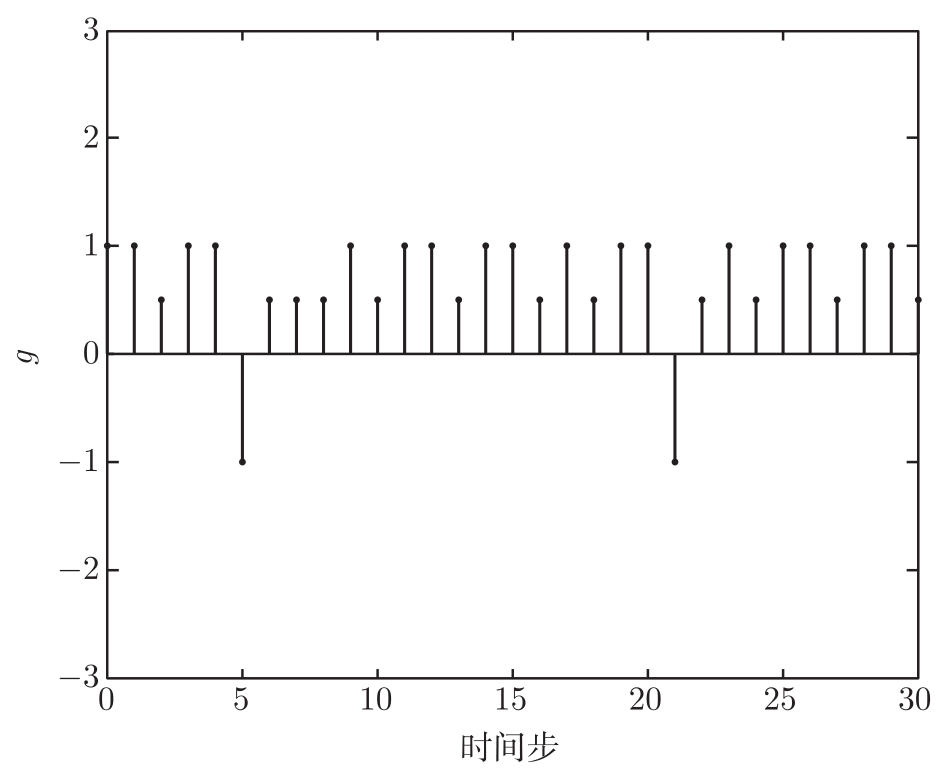
图4-9 当
p
=0.1时几乎处处渐进稳定条件下系统式(4-12)的状态
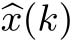 所处的区域
所处的区域